LeetCode - 1371 每个元音包含偶数次的最长子字符串（Java & JS & Python & C）

题目来源

1371. 每个元音包含偶数次的最长子字符串 - 力扣（LeetCode）

题目描述

给你一个字符串?s?，请你返回满足以下条件的最长子字符串的长度：每个元音字母，即?'a'，'e'，'i'，'o'，'u' ，在子字符串中都恰好出现了偶数次。

示例

示例 1

输入：s = "eleetminicoworoep"
输出：13
解释：最长子字符串是 "leetminicowor" ，它包含 e，i，o?各 2 个，以及 0 个 a，u 。

示例 2

输入：s = "leetcodeisgreat"
输出：5
解释：最长子字符串是 "leetc" ，其中包含 2 个 e 。

示例 3

输入：s = "bcbcbc"
输出：6
解释：这个示例中，字符串 "bcbcbc" 本身就是最长的，因为所有的元音 a，e，i，o，u 都出现了 0 次。

提示

• 1 <= s.length <= 5 x 10^5
• s?只包含小写英文字母。

题目解析

本题最简单的思路就是双循环暴力枚举所有子串，然后计算子串内各个元音的数目。

但是这种思路肯定会超时。

我们枚举子串的目的，是为了统计子串中各元音字符的数量，而实现该需求的更优思路是利用前缀和。

前缀和的应用场景有非常鲜明的特点，如求解连续范围内的状态，实际例子有：求解任意区间的和。

本题其实也可以当成前缀和问题来看，我们遍历输入串，每遍历一个字符，则对应位置 i 就有一个前缀状态 preSum[i]，本题preSum[i] 表示 [0, i] 范围内各个元音字符的数量，具体表现为：

preSum[i] = {
? ? ‘a’：aCount，

? ? 'e'：eCount，

? ? 'i'：iCount，

? ? 'o'：oCount，

? ? 'u'：uCount
}

那么，如果我们要求解范围[i, j]子串的各个元音的数量，即可通过 preSum[j] - preSum[i-1] 得到。
更多前缀和知识请看：算法设计 - 前缀和 & 差分数列_算法设计 - 前缀和 & 差分数列_伏城之外的博客-csdn博客-CSDN博客

但是光靠前缀和，我们还是要枚举所有子串，依旧会超时。

本题要求我们求解最长的子串，子串范围内各个元音数量为偶数。我们假设：

preSum[j] 位置各个元音的数量分别为：aCount偶数，eCount奇数，iCount偶数，oCount偶数，uCount奇数

再假设 [i, j] 范围内各个元音的数量都为偶数，那么此时preSum[i-1]的各个元音的数量应该是多少呢？

答：必然和preSum[j] 对应元音的数量同奇偶性。因为：

• 奇数 - 奇数 = 偶数
• 偶数 - 偶数 = 偶数

比如 preSum[j] = {aCount: 8,? eCount: 3, iCount: 6, oCount: 4, uCount: 5}；

且??preSum[i-1] =?{aCount: 2,? eCount: 1, iCount: 4, oCount: 2, uCount: 3}；

那么 [i, j] 范围内，各个元音的数量为：

• aCount = 8 - 2 = 6
• eCount = 3 - 1 = 2
• iCount = 6?- 4?= 2
• oCount = 4 - 2 = 2
• uCount = 5 - 3 = 2

因此，当我们得到 preSum[j] 后，我们应该在 i - 1 ∈ [0, j - 1] 范围内找到一个 preSum[i-1] 和 preSum[j] 的各个元音同奇偶性的，且 i - 1要最小，这样得到 [i, j] 范围子串才是 [0, j] 范围内一个最长的且各个元音数量都为偶数的子串。

此时，逻辑虽然得到了优化，但是我们依旧要遍历 0 ~ j - 1 范围内的位置 i，且需要对比对应 preSum[i] 和 preSum[j] 的各个元音的奇偶性，这样依然会超时。

接下来要用到状态压缩了。

由于我们只关注各个元音的数量的奇偶性，即每个元音的数量要么为奇数，要么为偶数，假设我们用0表示偶数，用1表示奇数的话。

那么初始 preSum[0] 的各个元音的状态就可以表示为二进制数：00000

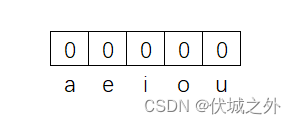
各个二进制位和对应元音对应，如上图所示，当二进制位值为0时，表示对应元音数量为偶数个，当二进制位值为1时，表示对应元音数量为奇数个。

这样我们就完成了 preSum[i] 的状态压缩。

那么状态压缩后的preSum[j] 和 preSum[j+1] 如何进行前缀和累进呢？

假设 j+1 位置的字符是 'e'，那么代表，preSum[j] 的二进制数 中 'e' 对应的位的性质反转，即奇变偶，偶变奇。

比如 preSum[j] = 01010，而 s[j+1] 字符是 'e'，则 preSum[j+1] = 00010

此时我们完全可以用异或运算从preSum[j]得出preSum[j+1]的结果，比如 s[j+1] == 'e'，则

preSum[j + 1] = preSum[j] ^ 01000

其中 01000 代表是新增一个'e'字符，同理

• 10000 代表新增一个 'a' 字符
• 01000 代表新增一个 'e' 字符
• 00100 代表新增一个 'i' 字符
• 00010 代表新增一个 'o' 字符
• 00001 代表新增一个 'u' 字符

接下来就是，比较preSum[i] 和 preSum[j] 的各个元音的奇偶性是否一致，就可以直接将对应二进制数进行值比较即可，值相同，则奇偶性一致，否则不一致。

比如：preSum[i-1] = 01010，preSum[j] = 01010，那么二者的各个元音的奇偶性就一致。

当我们完成preSum[i]的状态压缩后，我们就可以定义一个哈希表map来记录某个压缩状态最早出现的位置，map的key时压缩状态，val时该压缩状态的最早出现位置。

即：我们求解[0, j]范围前缀子串的压缩状态status = preSum[j]后：

• 如果map存在key=status，那么status状态最早出现位置为 map[staus]，我们定义 i = map[status]，那么i，j位置的前缀子串内部的各个元音的数量是同奇偶性的，即 [i+1, j] 范围内子串的各个元音的数量B必然都是偶数，[i+1, j] 范围子串是一个符合要求的子串，我们需要记录该子串的长度 j - (i + 1) + 1 = j - i
• 如果 map 不存在 key == status，那么status状态最早出现的位置就是 j，我们需要记录 map[status] = j

按照逻辑，我们只要遍历一遍字符串s，即可找到最长的目标子串。

JS算法源码

/**
 * @param {string} s
 * @return {number}
 */
var findTheLongestSubstring = function (s) {
  // "前缀子串"中各个元音的奇偶状态
  // 00000
  // aeiou
  // 元音字母和二进制位的对应关系如上，如果二进制位值位0，代表对应元音字符数量有偶数个，如果二进制位值为1，代表对应元音字符数量有奇数个
  // 初始未遍历时，没有子串，此时各个元音的数量都为0，即偶数个，因此所有二进制位值位0
  let status = 0b00000;

  // map记录某个状态的最早出现位置
  // 压缩状态用五位二进制数表示，因此最多有32种状态
  const map = new Array(32).fill(-2); // -2是一个不可能的位置,即初始时所有状态都未出现过
  // 00000 状态对应的十进制数为0，最早出现位置是-1，即未遍历，没有子串时
  map[0] = -1;

  // 记录最长的符合要求的子串长度
  let maxLen = 0;

  for (let i = 0; i < s.length; i++) {
    // 如果遍历的字符s[i]是元音字母，则变更对应二进制位的奇偶性
    switch (s[i]) {
      case "a":
        status ^= 0b10000;
        break;
      case "e":
        status ^= 0b01000;
        break;
      case "i":
        status ^= 0b00100;
        break;
      case "o":
        status ^= 0b00010;
        break;
      case "u":
        status ^= 0b00001;
        break;
    }

    // 如果对应状态的最早出现位置为-2，表示没有出现过对应状态，否则map[status]即status状态最早出现的位置
    if (map[status] != -2) {
      // 当前位置 i 的状态为status，而最早出现status状态的位置是 map[status]，两个位置同奇偶性，因此他们形成的范围内子串是符合要求的
      maxLen = Math.max(maxLen, i - map[status]);
    } else {
      // 如果对应状态之前未出现过，则当前位置 i 就是该状态的最早出现位置
      map[status] = i;
    }
  }

  return maxLen;
};

Java算法源码

import java.util.Arrays;

class Solution {
  public int findTheLongestSubstring(String s) {
    // "前缀子串"中各个元音的奇偶状态
    // 00000
    // aeiou
    // 元音字母和二进制位的对应关系如上，如果二进制位值位0，代表对应元音字符数量有偶数个，如果二进制位值为1，代表对应元音字符数量有奇数个
    // 初始未遍历时，没有子串，此时各个元音的数量都为0，即偶数个，因此所有二进制位值位0
    int status = 0b00000;

    // map记录某个状态的最早出现位置
    // 压缩状态用五位二进制数表示，因此最多有32种状态
    int[] map = new int[32]; // -2是一个不可能的位置
    Arrays.fill(map, -2);

    // 00000 状态对应的十进制数为0，最早出现位置是-1，即未遍历，没有子串时
    map[0] = -1;

    // 记录最长的符合要求的子串长度
    int maxLen = 0;

    for (int i = 0; i < s.length(); i++) {
      // 如果遍历的字符s[i]是元音字母，则变更对应二进制位的奇偶性
      switch (s.charAt(i)) {
        case 'a':
          status ^= 0b10000;
          break;
        case 'e':
          status ^= 0b01000;
          break;
        case 'i':
          status ^= 0b00100;
          break;
        case 'o':
          status ^= 0b00010;
          break;
        case 'u':
          status ^= 0b00001;
          break;
      }

      // 如果对应状态的最早出现位置为-2，表示没有出现过对应状态，否则map[status]即status状态最早出现的位置
      if (map[status] != -2) {
        // 当前位置 i 的状态为status，而最早出现status状态的位置是 map[status]，两个位置同奇偶性，因此他们形成的范围内子串是符合要求的
        maxLen = Math.max(maxLen, i - map[status]);
      } else {
        // 如果对应状态之前未出现过，则当前位置 i 就是该状态的最早出现位置
        map[status] = i;
      }
    }

    return maxLen;
  }
}

Python算法源码

class Solution(object):
    def findTheLongestSubstring(self, s):
        """
        :type s: str
        :rtype: int
        """
        # "前缀子串"中各个元音的奇偶状态
        # 00000
        # aeiou
        # 元音字母和二进制位的对应关系如上，如果二进制位值位0，代表对应元音字符数量有偶数个，如果二进制位值为1，代表对应元音字符数量有奇数个
        # 初始未遍历时，没有子串，此时各个元音的数量都为0，即偶数个，因此所有二进制位值位0
        status = 0b00000

        # map记录某个状态的最早出现位置, -2是一个不可能的位置, 即初始时各个状态都没有出现过
        # 压缩状态用五位二进制数表示，因此最多有32种状态
        map = [-2] * 32
        # 00000 状态对应的十进制数为0，最早出现位置是-1，即未遍历，没有子串时
        map[0] = -1

        # 记录最长的符合要求的子串长度
        maxLen = 0

        for i in range(len(s)):
            c = s[i]

            # 如果遍历的字符s[i]是元音字母，则变更对应二进制位的奇偶性
            if c == 'a':
                status ^= 0b10000
            elif c == 'e':
                status ^= 0b01000
            elif c == 'i':
                status ^= 0b00100
            elif c == 'o':
                status ^= 0b00010
            elif c == 'u':
                status ^= 0b00001

            # 如果对应状态的最早出现位置为-2，表示没有出现过对应状态，否则map[status]即status状态最早出现的位置
            if map[status] != -2:
                # 当前位置 i 的状态为status，而最早出现status状态的位置是 map[status]，两个位置同奇偶性，因此他们形成的范围内子串是符合要求的
                maxLen = max(maxLen, i - map[status])
            else:
                # 如果对应状态之前未出现过，则当前位置 i 就是该状态的最早出现位置
                map[status] = i

        return maxLen

C算法源码

int findTheLongestSubstring(char* s) {
    // "前缀子串"中各个元音的奇偶状态
    // 00000
    // aeiou
    // 元音字母和二进制位的对应关系如上，如果二进制位值位0，代表对应元音字符数量有偶数个，如果二进制位值为1，代表对应元音字符数量有奇数个
    // 初始未遍历时，没有子串，此时各个元音的数量都为0，即偶数个，因此所有二进制位值位0
    int status = 0b00000;

    // map记录某个状态的最早出现位置
    // 压缩状态用五位二进制数表示，因此最多有32种状态
    int map[32];
    for(int i=0; i<32; i++) map[i] = -2;  // -2是一个不可能的位置,即初始时所有状态都未出现过

    // 00000 状态对应的十进制数为0，最早出现位置是-1，即未遍历，没有子串时
    map[0] = -1;

    // 记录最长的符合要求的子串长度
    int maxLen = 0;

    int i=0;
    while(s[i] != '\0') {
        char c = s[i];

        // 如果遍历的字符s[i]是元音字母，则变更对应二进制位的奇偶性
        switch(c) {
            case 'a':
                status ^= 0b10000;
                break;
            case 'e':
                status ^= 0b01000;
                break;
            case 'i':
                status ^= 0b00100;
                break;
            case 'o':
                status ^= 0b00010;
                break;
            case 'u':
                status ^= 0b00001;
                break;
        }

        // 如果对应状态的最早出现位置为-2，表示没有出现过对应状态，否则map[status]即status状态最早出现的位置
        if (map[status] != -2) {
            // 当前位置 i 的状态为status，而最早出现status状态的位置是 map[status]，两个位置同奇偶性，因此他们形成的范围内子串是符合要求的
            maxLen = (int) fmax(maxLen, i - map[status]);
        } else {
            // 如果对应状态之前未出现过，则当前位置 i 就是该状态的最早出现位置
            map[status] = i;
        }

        i++;
    }

    return maxLen;
}