力扣日记12.21【二叉树篇】98. 验证二叉搜索树
发布时间:2023年12月21日
力扣日记:【二叉树篇】98. 验证二叉搜索树
日期:2023.12.21
参考:代码随想录、力扣
98. 验证二叉搜索树
题目描述
难度:中等
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
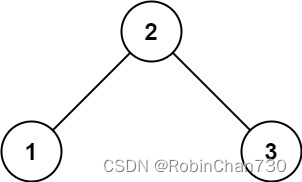
输入:root = [2,1,3]
输出:true
示例 2:
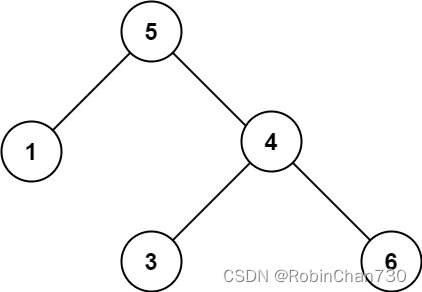
输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
- 树中节点数目范围在[1, 10^4] 内
- -2^31 <= Node.val <= 2^31 - 1
题解
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
#define SOLUTION 2
public:
#if SOLUTION == 0
// 下面代码有问题,搞不定了。。。
/*
bool isValidBST(TreeNode* root) {
if (root == nullptr) return false;
// 需要先对根节点进行处理
if (root->left != nullptr && root->left->val >= root->val) return false;
if (root->right != nullptr && root->right->val <= root->val) return false;
// 根节点暂且满足条件,递归判断其子树
return traversal(root->left, root->val, true) && traversal(root->right, root->val, false);
}
// 参数为当前子树的根节点,以及该子树的父节点的值,以及该子树是左子树还是右子树,返回值为该子树是否为二叉搜索树
bool traversal(TreeNode* root, int midNodeVal, bool leftTree) {
if (root == nullptr) return true;
// 左为空,则左不为false
// 左不为空,
if (root->left != nullptr) {
// 首先判断左子节点
if (root->left->val >= root->val) return false;
if (!leftTree) {
// 如果是右子树,还要保证其左节点比该子树的父节点大
if (root->left->val <= midNodeVal) return false;
}
}
if (root->right != nullptr) {
// 首先判断右子节点
if (root->right->val <= root->val) return false;
if (leftTree) {
// 如果是左子树,要保证其右节点比该子树的父节点小
if (root->right->val >= midNodeVal) return false;
}
}
// 遍历左右节点
bool left = traversal(root->left, root->val, true);
if (left == false) return false;
bool right = traversal(root->right, root->val, false);
return right;
}
*/
#elif SOLUTION == 1
// 思路:利用二叉搜索树的特性!!!
// 二叉搜索树中序遍历是有序的!!!
// 方式1:先转换为数组,再判断数组是否有序
bool isValidBST(TreeNode* root) {
// 先中序遍历得到数组
vector<int> result;
traversal(root, result);
// 对数组进行判断
// 如果数组为空或只有1个,则为true(空的树也为二叉搜索树!)
if (result.size() <= 1) return true;
// size >= 2
// 遍历数组
for (int i = 1; i < result.size(); i++) {
// 如果后面的元素 <= 前面的元素(注意也不能相等),则不是二叉搜索树
if (result[i] <= result[i-1]) return false;
}
return true;
}
// 中序遍历:左中右
void traversal(TreeNode* root, vector<int>& result) {
if (root == nullptr) return;
// 左
traversal(root->left, result);
// 中
result.push_back(root->val);
// 右
traversal(root->right, result);
}
#elif SOLUTION == 2
// 方式2:直接在进行中序遍历的同时判断是否有序
TreeNode* pre = nullptr; // 保存上一个节点(用来比较)
bool isValidBST(TreeNode* root) {
// 空,直接返回true
if (root == nullptr) return true;
// 左
bool left = isValidBST(root->left);
if (left == false) return false;
// 中
// 如果pre不为空,当前节点值需要比上一个节点值大
if (pre != nullptr && root->val <= pre->val) return false; // false 则不需要继续迭代了也不需要更新pre了
// 如果没有违反,更新pre,并继续递归
pre = root;
// 右
bool right = isValidBST(root->right);
return right;
}
#endif
};
复杂度
时间复杂度:
空间复杂度:
思路总结
- 本题就像是脑筋急转弯,得从二叉搜索树转到这样一个思路:
- 如果一棵树是二叉搜索树,其中序遍历一定是有序的!!!(从小到大)
- 因此,本题有两种方式来验证:
- 方式1:先用中序遍历(左中右)得到遍历数组;再对数组判断是否有序(较简单)
- 方式2:直接在中序遍历的同时判断是否有序(需要在递归中保存上一个值,稍复杂)
文章来源:https://blog.csdn.net/weixin_45847708/article/details/135141223
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 山海鲸可视化软件的优势:数据整合、可视化与个性化定制
- Linux调试分析诊断工具 strace
- 编写shell脚本运行jar包规避常见错误
- 亿赛通电子文档安全管理系统 SystemService XStream反序列化任意文件上传
- 自定义ORM:Python元类教程带你实现轻松数据库操作!
- 盘点Shein测评几大方式,怎么迅速入局Shein市场?
- Jackson进行Json反序列化对于一个小写字母开头后跟大写字母无法识别反序列成功问题
- SpringBoot教程(二) | 创建SpringBoot项目
- 初识react
- 如何查看崩溃日志