染色法判定二分图
发布时间:2023年12月26日
给定一个?n?个点?m?条边的无向图,图中可能存在重边和自环。
请你判断这个图是否是二分图。
输入格式
第一行包含两个整数?n?和?m。
接下来?m?行,每行包含两个整数?u?和?v,表示点?u?和点?v?之间存在一条边。
输出格式
如果给定图是二分图,则输出?Yes,否则输出?No。
数据范围
1≤n,m≤10^5
输入样例:
4 4
1 3
1 4
2 3
2 4
输出样例:
Yes什么叫二分图:
有两顶点集且图中每条边的的两个顶点分别位于两个顶点集中,每个顶点集中没有边直接相连接!
说人话的定义:图中点通过移动能分成左右两部分,左侧的点只和右侧的点相连,右侧的点只和左侧的点相连。

思路:

?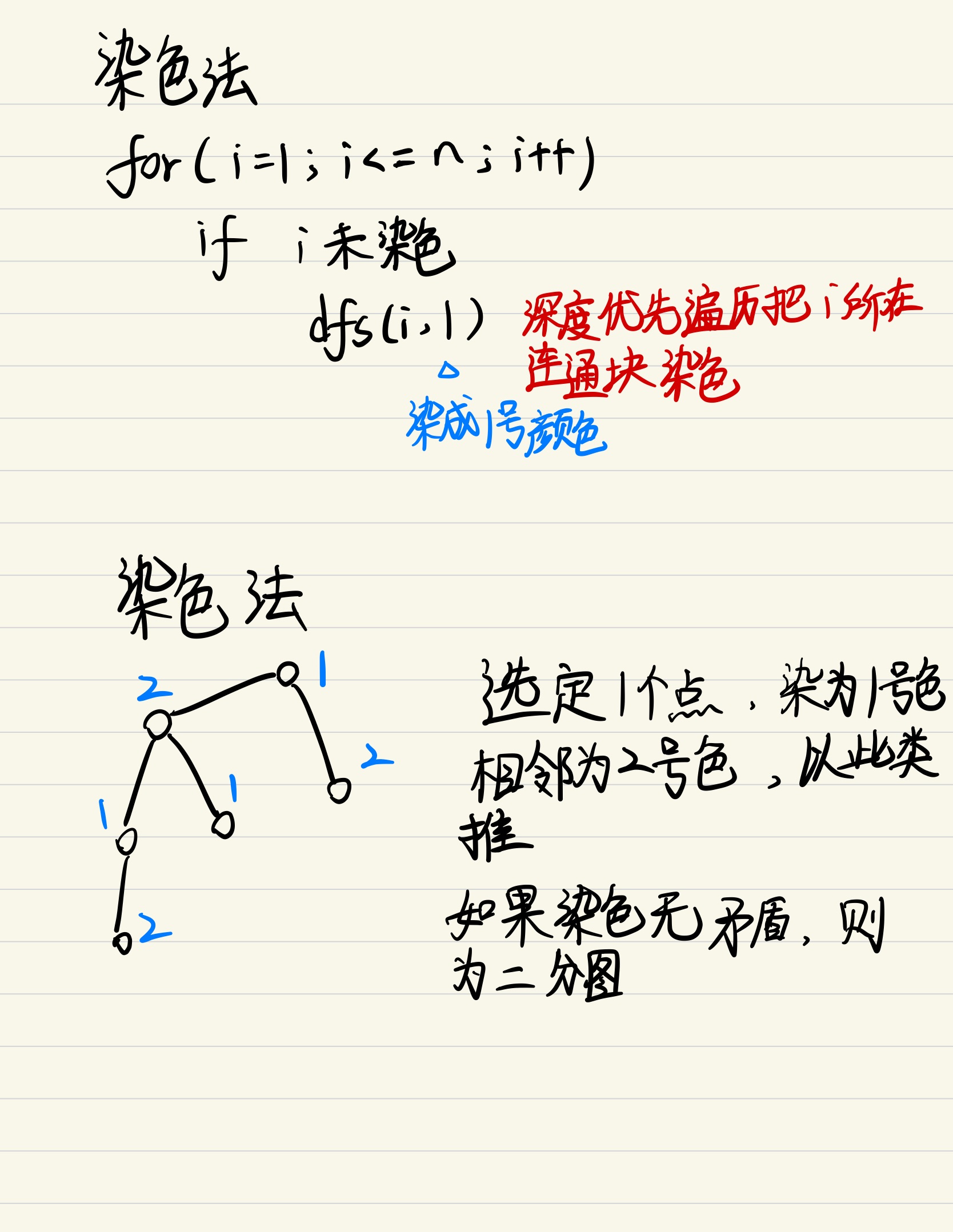
图中如果存在奇数环,那么这个图就不是二分图,染色法是一共有两种颜色,把相邻的点染成不同颜色,而我们可以通过染色法来判断这个图是否会出现矛盾,如果矛盾了就不是二分图。
示例代码:
//二分图:图中点通过移动能分成左右两部分,左侧的点只和右侧的点相连,右侧的点只和左侧的点相连
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1e5+10,M=2e5+10;
int n,m;
int h[N],e[M],ne[M],idx; //稀疏图用邻接表
int color[N]; //保存每个点的颜色,0是未染色,1是红色,2是黑色
void add(int a,int b) //增加一条a指向b的边
{
e[idx]=b;
ne[idx]=h[a];
h[a]=idx;
idx++;
}
bool dfs(int u,int c) //给u点和它所在的连通块进行染色,并返回染色之后这一个连通块是否矛盾的结果(true是没有矛盾)
{
color[u]=c; //把点u染成c色
for(int i=h[u];i!=-1;i=ne[i]) //遍历u相邻的点
{
int j=e[i]; //j是相邻的点的编号
if(!color[j]) //如果相邻的点没有染色,就递归处理这个相邻点
{
if(!dfs(j,3-c)) return false; // 3-1=2,如果u的颜色是1,则相邻点染成2,并给它的相邻点也染色
// 3-2=1,如果u的颜色是2,则相邻点染成1,并给它的相邻点也染色
//如果给相邻点染色发生错误,就有矛盾
}
else if(color[j]==c) return false; //如果相邻点染色和u点颜色一样,就出现了矛盾
}
return true;
}
int main()
{
scanf("%d%d",&n,&m);
memset(h,-1,sizeof(h));
while(m--)
{
int a,b;
scanf("%d%d",&a,&b);
add(a,b),add(b,a); //无向图
}
bool flag=true;
for(int i=1;i<=n;i++) //遍历所有点
{
if(!color[i]) //如果这个点还没有染色
{
if(!dfs(i,1)) //把这个点染成1号色,并递归处理所有相邻点
{
flag=false; //出现了矛盾(相邻的点染了一样的色)
break;
}
}
}
if(flag) puts("Yes"); //染色没有矛盾,即为二分图
else puts("No");
return 0;
}注意:
bool dfs(int u,int c) //给u点和它所在的连通块进行染色,并返回染色之后这一个连通块是否矛盾的结果(true是没有矛盾)
{
color[u]=c; //把点u染成c色
for(int i=h[u];i!=-1;i=ne[i]) //遍历u相邻的点
{
int j=e[i]; //j是相邻的点的编号
if(!color[j]) //如果相邻的点没有染色,就递归处理这个相邻点
{
if(!dfs(j,3-c)) return false; // 3-1=2,如果u的颜色是1,则相邻点染成2,并给它的相邻点也染色
// 3-2=1,如果u的颜色是2,则相邻点染成1,并给它的相邻点也染色
//如果给相邻点染色发生错误,就有矛盾
}
else if(color[j]==c) return false; //如果相邻点染色和u点颜色一样,就出现了矛盾
}
return true;
}
上面这段dfs代码是给当前点和所在的连通块染色,并判断染完色这个连通块有没有出现矛盾,矛盾了就不是二分图。?
文章来源:https://blog.csdn.net/weixin_63504072/article/details/135209756
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章