Mysql易错部分

1.select中字段是否必须出现在groupby中

group by中的字段可以不出现在select中,但是select中只能有group by中的字段和函数.，不严谨看下select @@sql_mode; ?查看查看sql_mode

  select
            a.user_name,
            a.job_number,
            a.geography,
           b.total_planned ,
            sum(case when YEARWEEK(c.create_time , 1)= YEARWEEK(now() , 1) and c.inviter_code is not null then 1 else 0 end ) as total_week,
            count(1) as total_already,
            concat(round(count(1)/ b.total_planned*100, 2), '%')as progress
        from
        tt1 as b
        left join tt2 as a on
        a.job_number = b.job_number
        left join user_basic_info c on
        a.job_number = c.inviter_code
        group by
            a.job_number,
            a.geography,
            b.total_planned
        order by a.geography,a.job_number
-- select @@sql_mode;  查看查看sql_mode
--- 下列为结果ONLY_FULL_GROUP_BY,STRICT_TRANS_TABLES,NO_ZERO_IN_DATE,NO_ZERO_DATE,ERROR_FOR_DIVISION_BY_ZERO,NO_ENGINE_SUBSTITUTION
 

ONLY_FULL_GROUP_BY：提示必须在select中完整出现，其他的可以是聚合函数形式

2.select加锁分析

锁类型

共享锁(S锁):假设事务T1对数据A加上共享锁，那么事务T2可读不可写。
排他锁(X锁):假设事务T1对数据A加上排他锁，那么事务T2读写均不可。

update、delete等语句加上的锁都是行级别的锁。只有LOCK TABLE … READ??和? ?LOCK TABLE … WRITE才能申请表级别的锁。
意向共享锁(IS锁):一个事务在获取（任何一行/或者全表）S锁之前，一定会先在所在的表上加IS锁。
意向排他锁(IX锁):一个事务在获取（任何一行/或者全表）X锁之前，一定会先在所在的表上加IX锁。

意向锁存在的目的。假设事务T1，用X锁来锁住了表上的几条记录，那么此时表上存在IX锁，即意向排他锁。那么此时事务T2要进行LOCK TABLE … WRITE的表级别锁的请求，可以直接根据意向锁是否存在而判断是否有锁冲突

快照读和当前读

在mysql中select分为快照读和当前读，执行下面的语句

select * from table where id = ?;

执行的是快照读，读的是数据库记录的快照版本，是不加锁的。（这种说法在隔离级别为Serializable中不成立）
那么，执行

select * from table where id = ? lock in share mode;

会对读取记录加S锁 (共享锁)，执行

select * from table where id = ? for update

会对读取记录加X锁 (排他锁)

加的是表锁还是行锁呢？ 下述详细过程

【原创】惊！史上最全的select加锁分析(Mysql)_weixin_30951389的博客-CSDN博客

3.二叉树大概认识

如图：

左子树所有的节点都小于父节点，右子树所有的节点都大于父节点。投影到平面以后，就是一个有序的线性表。?[绿色模块]

可看做已经排好序列！只不过树的结构组织起来！

学过java开发的一定了解：数组+单链表结构 ；勾结两者优缺点 二叉树出现了!

优点：兼顾了有序数组和链表的优点：二叉查找树既能够实现快速查找，又能够实现快速插入

缺点：查找耗时是和这棵树的深度相关的，在最坏的情况下时间复杂度会退化成O(n)

【最坏的情况，糖葫芦样式，你就说深不深】

二叉树变成了一个链表结构(我们把这种树叫做“斜树”),这种情况下不能达到加快检索速度的目的，和顺序查找效率是没有区别的。如果我要查6，那么这需要遍历所有元素来找出最大值。这是一项线性时间的操作，或称O(n)时间

造成它倾斜的原因是什么呢？
因为左右子树深度差太大，这棵树的左子树根本没有节点——也就是它不够平衡。

3.1平衡二叉树来了

所以，我们有没有左右子树深度相差不是那么大，更加平衡的树呢？
这个就是平衡二叉树，叫做 Balanced binary search trees，或者 AVL 树（AVL 是
发明这个数据结构的人的名字）。

?定义：左右子树深度差绝对值不能超过 1。

比如左子树的深度是 2，右子树的深度只能是 1 或者 3。、

3.2 平衡二叉树是如何保证“平衡”的呢？

示例：
插入 1、2、3。当我们插入了 1、2 之后，如果按照二叉查找树的定义，3 肯定是要在 2 的右边的，这个时候根节点 1 的右节点深度会变成 2，但是左节点的深度是 0，因为它没有子节点，所以就会违反平衡二叉树的定义。
那应该怎么办呢?因为它是右节点下面接一个右节点，右-右型，所以这个时候我们 要把 2 提上去，这个操作叫做左旋。 反之左-左型叫做右旋

?

?3.3平衡二叉树（AVL树）节点存储了那些内容

• 索引的键值?????????比如我们在 id 上面创建了一个索引，我在用 where id =1 的 条件查询的时候就会找到索引里面的 id的这个键值。
• 数据的磁盘地址? ?索引的作用就是去查找数据的存放的地址
• 左子节点和右子节点的引用? ?可找到下个节点

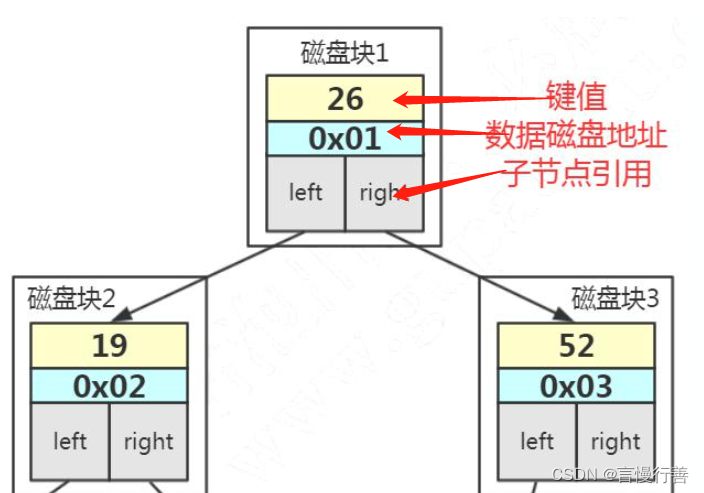
??3.4? ? ? ? B? Tree树前的问题

mysql的存储结构分为：表空间、段、簇（区）、页、行

?# 查看有多少个数据页

show variables like 'innodb_page_size';

往表中插入数据时，如果一个页面已经写完，产生一个新的叶页面。如果一个簇的 所有的页面都被用完，会从当前页面所在段新分配一个簇。
如果数据不是连续的，往已经写满的页中插入数据，会导致叶页面分裂:

• 行 Row
  InnoDB 存储引擎是面向行的(row-oriented)，也就是说数据的存放按行进行存放。

1.用树的结构来存储索引的时候，访问一个节点就要跟磁盘之间发生一次 IO。
InnoDB 操作磁盘的最小的单位是一页（或者叫一个磁盘块），大小是16K(16384 字节)。

2.

一个节点只存一个键值+数据+引用，例如整形的字段，可能只用了十几个
或者几十个字节，它远远达不到 16K 的容量，所以访问一个树节点，进行一次 IO 的时候，浪费了大量的空间

所以如果每个节点存储的数据太少，从索引中找到我们需要的数据，就要访问更多
的节点，意味着跟磁盘交互次数就会过多。

3.5AVL 树与 B? Tree图形对比

同样是插入17个元素，AVL树已经5层的深度了，而BTree才4层，如果数据越多，这个对比是越来越明显的?

?3.6B Tree【多路平衡查找树—Balanced? Tree】 一个节点多个元素

特点：

1.跟 AVL 树一样，B 树在枝节点和叶子节点存储键值、数据地址、节点引用。

2.分叉数（路数）永远比关键字数多 1。比如每个节点存储两个关键字，那么就会有三个指针指向三个子节点

关键字：子节点的引用? N

路数：分叉 N+1

3.7 B +Tree ***

1.关键字的数量是跟路数（度degree）相等的
2.B+Tree 的根节点和枝节点中都不会存储数据，只有叶子节点才存储数据。搜索到关键字不会直接返回，会到最后一层的叶子节点。
3.B+Tree 的每个叶子节点增加了一个指向相邻叶子节点的指针，它的最后一个数据会指向下一个叶子节点的第一个数据，形成了一个有序链表的结构
4.它是根据左闭右开的区间 [ )来检索数据。

3.8?B +Tree存储数据量

假设一条记录是 1K，一个叶子节点(一页)可以存储 16 条记录。非叶子节点可以存储多少个指针?
假设索引字段是 bigint 类型，长度为 8 字节。指针大小在 InnoDB 源码中设置为 6 字节，这样一共 14 字节。非叶子节点(一页)可以存储 16384/14=1170 个这样的单元(键值+指针)，代表有 1170 个指针。
树深度为 2 的时候，有 1170^2 个叶子节点，可以存储的数据为 1170117016=21902400。
在查找数据时一次页的查找代表一次 IO，也就是说，一张 2000 万左右的表，查询数据最多需要访问 3 次磁盘。
所以在 InnoDB 中 B+ 树深度一般为 1-3 层，它就能满足千万级的数据存储。

4.推荐文章 比较全

Mysql_依剑行走天下的博客-CSDN博客