动手学深度学习5 矩阵计算
课程安排:

视频:https://www.bilibili.com/video/BV1eZ4y1w7PY/?spm_id_from=autoNext&vd_source=eb04c9a33e87ceba9c9a2e5f09752ef8
课件:https://zh-v2.d2l.ai/chapter_preliminaries/calculus.html
课上PPT:https://courses.d2l.ai/zh-v2/assets/pdfs/part-0_6.pdf
机器学习或深度学习中,所有优化模型的求解都是通过求导数来进行的。
导数 偏导数 微分 梯度 这些数学概念先了解一些方便理解。先理解一下课件。
1. 导数和微分
斜率:导数的意义。

图片下方的是一些链式法则。
h足够小 逼近
%matplotlib inline
import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2l
def f(x):
return 3*x**2 - 4*x
def numerical_lim(f, x, h):
return (f(x+h) - f(x))/h
h = 0.1
for i in range(5):
print(f'h={h:.5f}, numerical limit={numerical_lim(f, 1, h):.5f}')
h*=0.1
h=0.10000, numerical limit=2.30000
h=0.01000, numerical limit=2.03000
h=0.00100, numerical limit=2.00300
h=0.00010, numerical limit=2.00030
h=0.00001, numerical limit=2.00003
2. 偏导数
不一定存在导数怎么办

3. 梯度
要把形状搞对

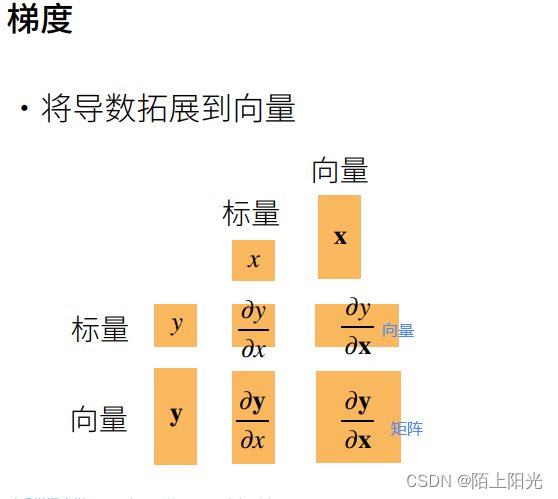
1. 向量-标量求导
具体是怎么变化的:
x是一个列向量,y是一个标量,关于标量y关于列向量x的导数是一个行向量。第i个元素,是标量y关于标量
x
i
x_{i}
xi?的导数。
对于
(
x
1
,
x
2
)
=
(
1
,
1
)
(x_{1}, x_{2})=(1,1)
(x1?,x2?)=(1,1)这个点,对等高线做切线,切线做正交的方向,方向的值是(2,4),和等高线正交,和梯度的值【梯度带入(1,1)是(2,4)】一致,也是梯度的方向。
即梯度是和等高线正交的方向,指向的是值变化最大的方向,通常是往大的值走,是后续所有机器学习求解的核心思想。

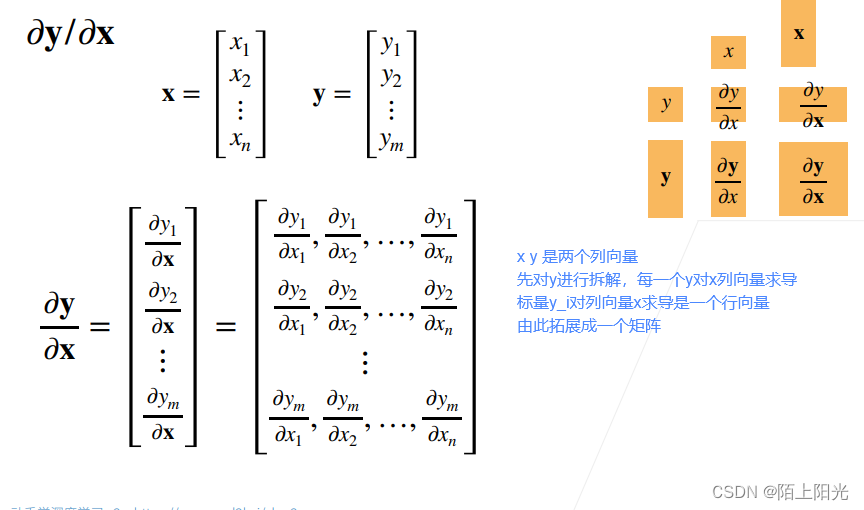
向量关于向量的导数,是一个矩阵。

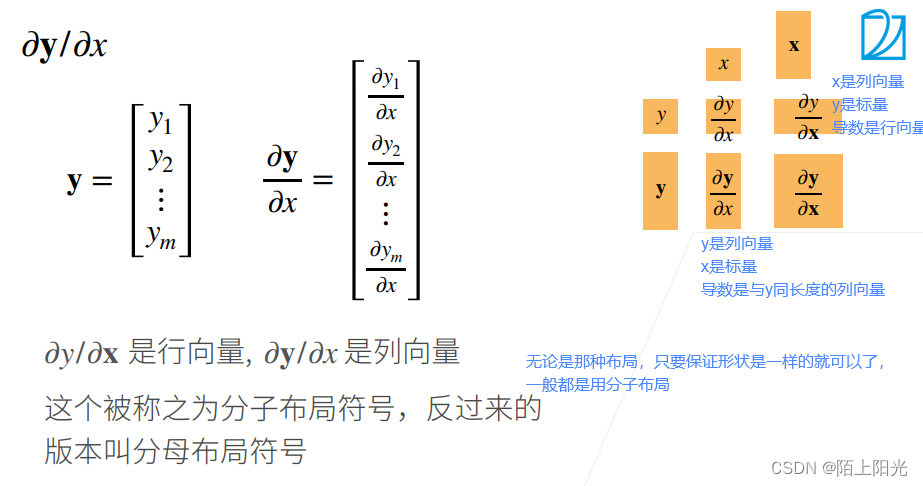
2. 向量-向量求导

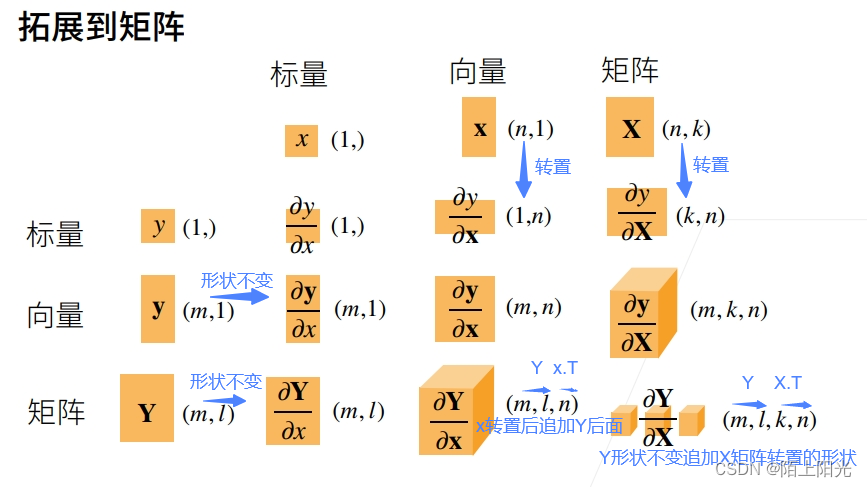
3. 拓展到矩阵
用二维数组区分行向量跟列向量
4. 链式法则

5. 小结

QA
- 导数主要用于梯度下降,容易陷入局部最优解,有办法达到全局最优解吗?
如果是凸函数,能拿到全局最优解,但是机器学习几乎不会处理凸函数,基本上拿不到全局最优解【理论上数学上可以,但计算上基本拿不到】。机器学习不关注P问题,关注NP问题。
在计算机科学中,P和NP是两个常见的复杂性类别。它们用于描述问题的计算复杂性。
P问题(P class)指的是那些可以在多项式时间内解决的问题。多项式时间是指问题的解决时间与问题规模的多项式成正比。P问题通常可以在合理的时间内通过确定性算法求解。
NP问题(NP class)指的是那些可以在多项式时间内验证解答的问题。换句话说,如果给定一个解决方案,我们可以在多项式时间内验证它的正确性。然而,我们不能保证在多项式时间内找到一个解决方案。因此,NP问题可能需要指数时间或更长时间来解决。
机器学习通常关注的是解决NP问题,即那些不能在多项式时间内确定性解答的问题。机器学习使用各种技术和方法,例如优化算法、近似算法和启发式算法,来尝试在合理的时间内找到可能的解决方案。
- pytorch不用做手动微分,有自动微分的工具包。重要的是关注:导数的形状和input的形状是怎么变化的,有什么关系。
练习

这章节还是得回去学习导数相关的数学知识才能更好的理解~~QAQ
1.
def use_svg_display():
"""使用svg格式在jupyter中显示绘图"""
backend_inline.set_matplotlib_formats('svg')
def set_figsize(figsize=(3.5, 2.5)):
"""设置matplotlib的图表大小"""
use_svg_display()
d2l.plt.rcParams['figure.figsize'] = figsize
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
"""设置matplotlib的轴"""
axes.set_xlabel(xlabel)
axes.set_ylabel(ylabel)
axes.set_xlim(xlim)
axes.set_ylim(ylim)
axes.set_xscale(xscale)
axes.set_yscale(yscale)
if legend:
axes.legend(legend)
axes.grid()
def plot(X, Y=None, xlabel=None, ylabel=None, legend=None, xlim=None, ylim=None, xscale='linear', yscale='linear', fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
"""绘制数据点"""
if legend is None:
legend = []
set_figsize(figsize)
# 用于获取当前图形的坐标轴对象(gca代表get current axis)。它的功能是返回当前图形的坐标轴对象,以便我们可以对坐标轴进行各种设置和操作,例如设置坐标轴范围、标签、标题,添加图例等。使用d2l.plt.gca()函数可以方便地对当前图形的坐标轴进行自定义操作。
axes = axes if axes else d2l.plt.gca()
# 如果X有一个轴 输出True
def has_one_axis(X):
return (hasattr(X, 'ndim') and X.ndim == 1 or isinstance(X, list) and not hasattr(X[0], "__len__"))
if has_one_axis(X):
X = [X]
if Y is None:
X, Y = [[]] * len(X), X
elif has_one_axis(Y):
Y = [Y]
if len(X) != len(Y):
X = X * len(Y)
axes.cla() # Matplotlib 中的一个函数,用于清除(clear)当前坐标轴(axes)中的所有内容 以便重新制作
for x, y, fmt in zip(X, Y, fmts):
if len(x):
axes.plot(x, y, fmt)
else:
axes.plot(y, fmt)
set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)
def f(x):
return x**3 - x**(-1)
x = np.arange(0, 3, 0.1)
plot(x, [f(x), 4*x-4], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])
感觉有点对了,不知道为什么np.arange(-10, 10, 0.1)设置的话,图片就很奇怪,看着都不对。
Y 输入的是两个 [f(x), 切线方程]
切线方程:导数代入值得斜率,原函数带入值得点,一点一斜率写出切线【直线】方程
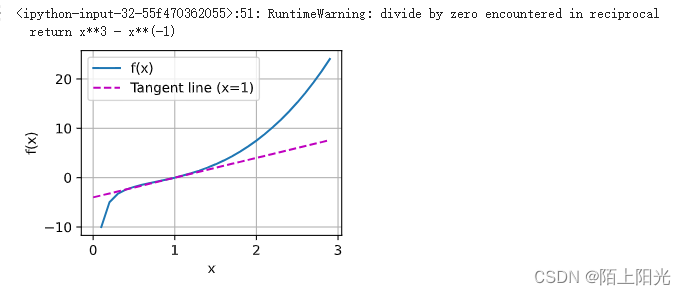
找了个别的写法
import numpy as np
import matplotlib.pyplot as plt
# 定义函数 f(x) 和其导数 f'(x)
def f(x):
return x**3 - x**(-1)
def f_derivative(x):
return 3*x**2 + x**(-2)
# 创建等间距数据点
x = np.linspace(0, 3, 10, dtype=float)
y = f(x)
# 计算切线的值
tangent_x = np.array([1], dtype=float)
tangent_y = f(tangent_x) + f_derivative(tangent_x) * (x - tangent_x)
# 绘制函数和切线图像
plt.plot(x, y, label='f(x)=x^3 - x^(-1)')
plt.plot(x, tangent_y, label='Tangent Line at x=1')
plt.scatter(tangent_x, f(tangent_x), color='red', label='Tangent Point (1, f(1))')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
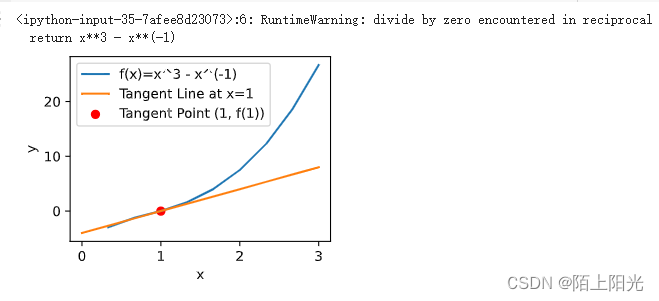
-
求函数 f ( x ) = 3 ? x 1 2 + 5 ? e x 2 f(x)=3*x_{1}^2+5*e^{x_{2}} f(x)=3?x12?+5?ex2?的梯度
要求函数 f ( x ) = 3 ? x 1 2 + 5 ? e x 2 f(x)=3*x_{1}^2+5*e^{x_{2}} f(x)=3?x12?+5?ex2?的梯度,我们需要对每个变量求偏导数。
函数f(x)对x1的偏导数可以通过求导公式得到: ?f/?x1 = 6x1
函数f(x)对x2的偏导数可以通过求导公式得到: ?f/?x2 = 5e^x2
因此,函数f(x)的梯度为 (?f/?x1, ?f/?x2) = (6x1, 5e^x2) -
没搞明白 有大佬会的能不能评论区写一写
-
写出函数u=f(x,y,z), 其中 x=x(a,b), y=y(a,b), z=z(a,b)的链式法则
根据链式法则,函数u关于自变量a和b的偏导数可以表示为:
?u/?a = (?f/?x)(?x/?a) + (?f/?y)(?y/?a) + (?f/?z)(?z/?a)
?u/?b = (?f/?x)(?x/?b) + (?f/?y)(?y/?b) + (?f/?z)(?z/?b)
这里,?u/?a 表示函数u对变量a的偏导数,?u/?b 表示函数u对变量b的偏导数。?f/?x 表示函数f对变量x的偏导数,依此类推。
所以,链式法则可以用来计算复合函数的偏导数
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!