统计学-R语言-6.2

---

前言

本篇将继续介绍上篇所剩下的内容。

---

总体均值的区间估计

两个总体均值之差的估计

设两个总体的均值分别为?1和?2，从两个总体中分别抽取样本量为n1和n2的两个随机样本，其样本均值分别为 和 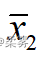。估计两个总体均值之差（u1-u2）的点估计量显然是两个样本的均值之差（ ）。
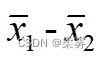两个总体均值的置信区间是由两个样本均值之差加减估计误差得到的。
两个总体均值之差(?1-?2)在置信水平下的置信区间可一般性地表达为：

两个总体均值之差的估计（独立大样本的估计）

假定条件
两个总体都服从正态分布，?1２、 ?2２已知
若不是正态分布, 可以用正态分布来近似(n1?30和n2?30)
两个样本是独立的随机样本
使用正态分布统计量 z

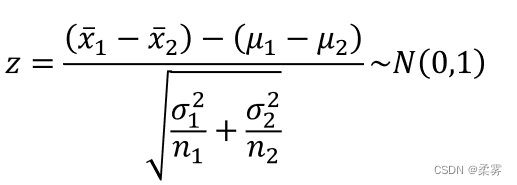
例题：
为研究男女工资的差异，从某行业中随机抽取男女员工各40人，得到的月工资数据如下表所示。建立男女平均工资之差的95%的置信区间。（example5_3）

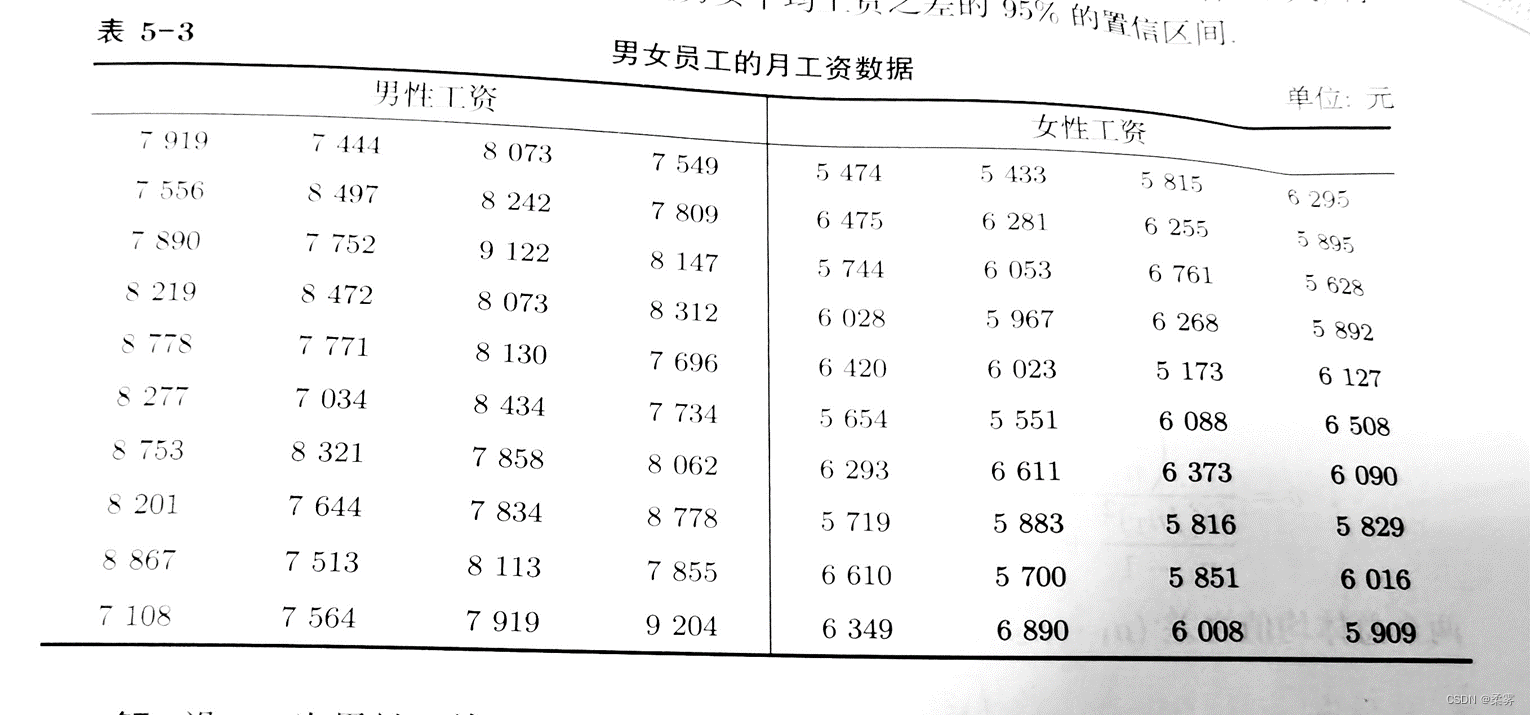
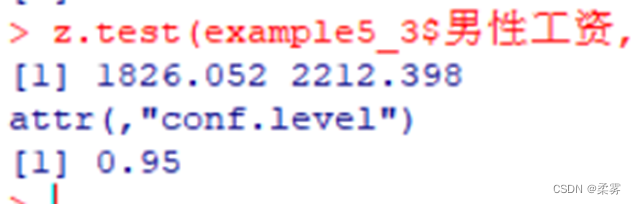
load("C:/example/ch5/example5_3.RData")
library(BSDA)
z.test(example5_3$男性工资,example5_3$女性工资,sigma.x=sd(example5_3$男性工资),sigma.y=sd(example5_3$女性工资))$conf.int

两个总体均值之差的估计（独立小样本的估计）

假定条件
两个总体都服从正态分布
两个总体方差已知(,)
两个独立的小样本(n1<30和n2<30)
两个样本均值之差经标准化后服从标准正态分布，此时可按下式建立两个总体均值之差的置信区间。

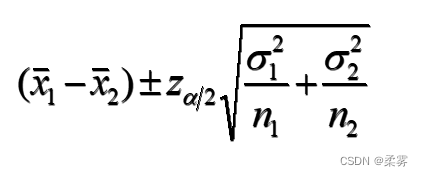
当和未知的时候，有以下几种情形：
(1) 两个总体方差未知但相等：

需要用两个样本的方差 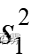和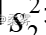
来估计。这时，需要将两个样本的数据合并在一起，得到的合并估计量 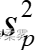，其计算公式如下：

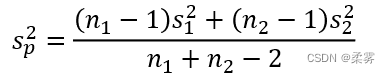
这时，两个样本均值之差经标准化后服从自由度为(n1+n2-2)的t分布。

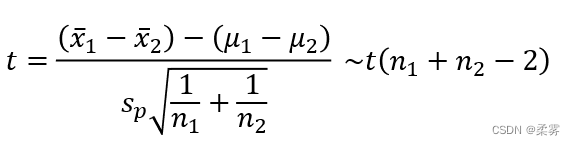
例题：
（数据： example5_4. RData）为估计两种方法组装产品所需时间的差异，分别对两种不同的组装方法各随机安排12个工人，每个工人组装一件产品所需的时间如下表所示。假定两种方法组装产品的时间服从正态分布，求以95%的置信水平建立两种方法组装产品所需平均时间差值的置信区间。

平均时差95%的置信区间(使用t.test函数)
假设方差相等

load("C:/example/ch5/example5_4.RData")
t.test(x=example5_4$方法一,y=example5_4$方法二,var.equal=TRUE)$conf.int

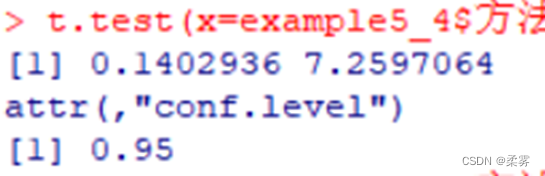
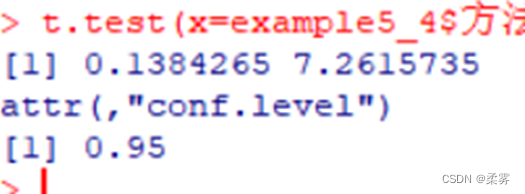
假设方差不相等

t.test(x=example5_4$方法一,y=example5_4$方法二,var.equal=FALSE)$conf.int

两个总体均值之差的估计（配对样本的估计）

在上面的例题中，使用的是两个独立样本。但使用独立样本估计两个总体均值之差时有潜在弊端：比如，在对每种方法随机指派12个工人时，偶尔可能会将技术比较差的12个工人指派给方法一，而技术较好的12个工人指派给方法二。这种不公平的指派可能会掩盖两种方法组装产品所需时间的真正差异。
为解决这一问题，可以使用配对样本（paired sample），即一个样本中的数据与另一个样本中的数据相对应，这样的数据通常是对同一个体所做的前后两次测量。比如，先指定12个工人用第一种方法组装产品，然后再让这12个工人用第二种方法组装产品，再比如：比如减肥前后的重量比较，治疗前后的症状比较，同样情况下对两种材料某种性能的比较等等，这样得到的两种方法组装产品的时间数据就是配对数据。

例题：

（数据：example5_5. RData）由10名学生组成一个随机样本，让他们分别采用A和B两套试卷进行测试，结果如下表所示。假定两套试卷分数之差服从正态分布，试建立两种试卷平均分数之差 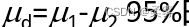的置信区间。

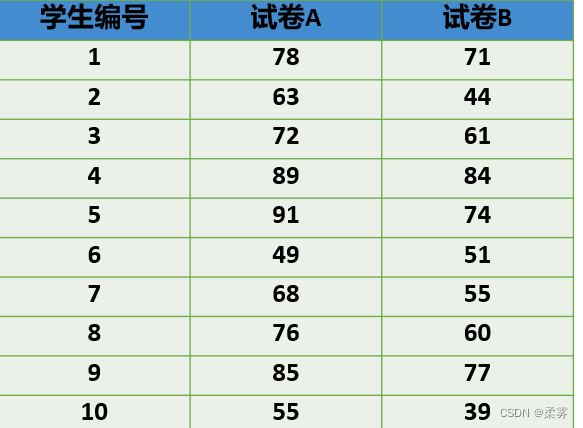
试卷平均分数差值95%的置信区间

load("C:/example/ch5/example5_5.RData")
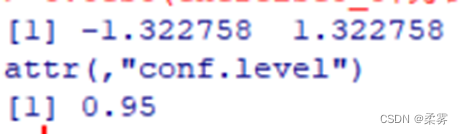
t.test(example5_5$试卷A,example5_5$试卷B,paired=TRUE)    

只输出置信区间信息

t.test(example5_5$试卷A,example5_5$试卷B,paired=TRUE)$conf.int

例题：
一个有20人参加的技术革新试验前后的产量列在下表中，这里，pre和post分别是试验前后的产量(单位：个)，而D=post-pre为相应的差 值(单位：个)。

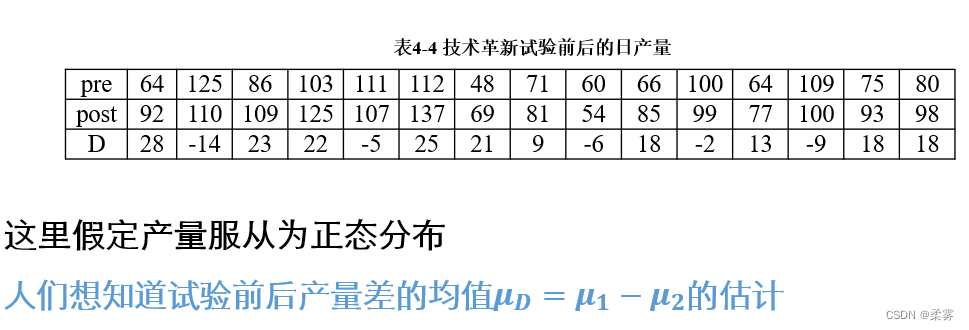
首先看看试验前后的产量的线图，结果如下所示：

pre=c(64,125,86,103,111,112,48,71,60,66,100,64,109,75,80)
post=c(92,110,109,125,107,137,69,81,54,85,99,77,100,93,98)
production=cbind(pre,post)#cbind是根据列进行合并，合并的前提是所有数据行数相等,构建分块矩阵
matplot(production,type="o",col=1,pch=c(1,16),ylab="production")#matplot()函数将两个矩阵作为参数。一个矩阵的列参照另一个矩阵的相应列来绘制图形。在绘制同一个图时，两个矩阵的行数应该一样。如果行数不一样，行数较少的那个矩阵用缺失值（NA）来填充。第一个矩阵的值会用在横轴上。如果其中x,y一人失踪，另一种是作为y和x向量1:n使用。遗漏值（NAS）是允许的。pch点的样式，1个字符或整数的字符串或向量绘图字符，请参阅points。第一个字符是绘制的第一个图，第二次为第二个字符，默认为数字（1，0到9），然后是小写和大写字母。col,颜色矢量。颜色循环使用。
legend(8,130,c("技术革新前的产量","技术革新后的产量"),pch=c(1,16),lty=1:2)#legend(x, y, legend)在点(x,y)处添加图例,说明内容由legend给定

可以看出，技术革新前后的产量在 大部分情况下的走势相似，这表明一 个人在技术革新前后的产量并不是独立的。相比于技术革新前，大部分的工人都在技术革新后有更高的产量，因此，这个问题不能用前面对待两个独立样本的方法来求估计。
可以把同一个个体观察前后的产量相减，对得到的差使用正态总体均值的区间估计来解决

可以看出，技术革新前后的产量在 大部分情况下的走势相似，这表明一 个人在技术革新前后的产量并不是独立的。相比于技术革新前，大部分的工人都在技术革新后有更高的产量，因此，这个问题不能用前面对待两个独立样本的方法来求估计。
可以把同一个个体观察前后的产量相减，对得到的差使用正态总体均值的区间估计来解决。

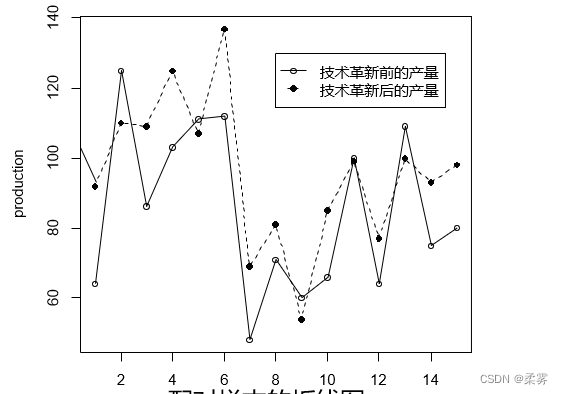
mean(post-pre)  

[1] 10.8

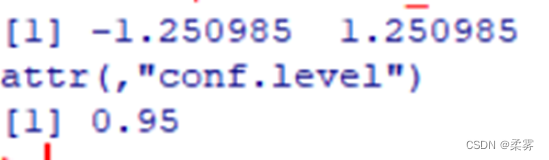
t.test(post-pre)$conf  #或者使用等价的语t.test(x,y,parired=T)$conf,可以得到同样的结果 

[1] 3.038022 18.561978

attr(,"conf.level")  

[1] 0.95

总体比例的区间估计

总体比例的区间估计研究一个总体时，推断总体比例π使用的统计量为样本比例p。研究两个总体时，所关注的参数是两个总体的比例之差（ ），用于推断的统计量则是两个样本的比例之差（ ）。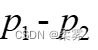

总体比例的区间估计(一个总体比例的估计）

推断总体比例时，同样需要考虑样本量的大小。当样本量非常大时，可采用传统的估计方法。对于小样本或中等大小的样本，需要对样本量和试验成功的次数做出修正以改进估计的区间。
大样本情形：

例题：
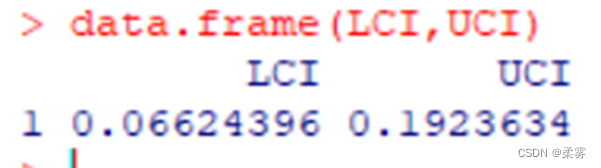
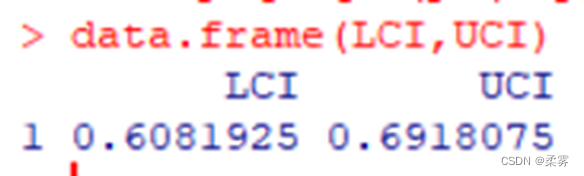
某城市想要进行一项交通措施改革，为征求市民对该项改革措施的意见，在成年人中随机调查了500个市民，其中325人赞成改革措施。用95%的置信水平估计该城市成年人口中赞成该项改革的人数比例的置信区间。

n<-500;x<-325;p<-x/n
q<-qnorm(0.975)
LCI<-p-q*sqrt(p*(1-p)/n)
UCI<-p+q*sqrt(p*(1-p)/n)
data.frame(LCI,UCI)

任意大小样本情形：
大样本的估计方法至今仍被广泛使用，但按该方法计算出来的置信水平为(1- ) 的置信区间能够覆盖总体真实比例的概率通常小于(1- )，即使大样本也是如此（除非样本量非常大），更不可能应用于小样本。因此对于任意大小的样本，可以通过修正试验次数（样本量）n和样本比例的值让置信区间有所改进。

任意大小样本情形：

例题：
某城市想要进行一项交通措施改革，为征求市民对该项改革措施的意见，在成年人中随机调查了500个市民，其中325人赞成改革措施。用95%的置信水平估计该城市成年人口中赞成该项改革的人数比例的置信区间。
女性与男性收视率差值的95%置信区间(大样本)

n1<-500+4
p1<-(325+2)/n1
q<-qnorm(0.975)
LCI<-p1-q*sqrt(p1*(1-p1)/n1)
UCI<-p1+q*sqrt(p1*(1-p1)/n1)
data.frame(LCI,UCI)

总体比例的区间估计(两个总体比例之差的估计)

对两个总体比例之差的估计同样需要考虑两个样本量的大小。当两个样本量都非常大时，可采用传统的估计方法。对于两个小样本或中等大小的样本，需要对样本量和试验成功的次数做出修正以改进估计的区间。

假定条件


例题：
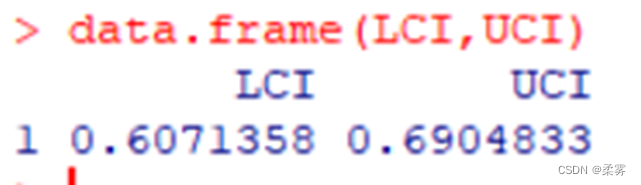
在某个电视节目的收视率调查中，女性观众随机调查了500人，有225人收看了该节目；男性观众随机调查了400人，有128人收看了该节目。用95%的置信水平估计女性与男性收视率差值的置信区间。
女性与男性收视率差值的95%置信区间(大样本)

p1<-225/500;p2<-128/400
q<-qnorm(0.975)
LCI<-p1-p2-q*sqrt(p1*(1-p1)/500+p2*(1-p2)/400)
UCI<-p1-p2+q*sqrt(p1*(1-p1)/500+p2*(1-p2)/400)
data.frame(LCI,UCI)

例题：
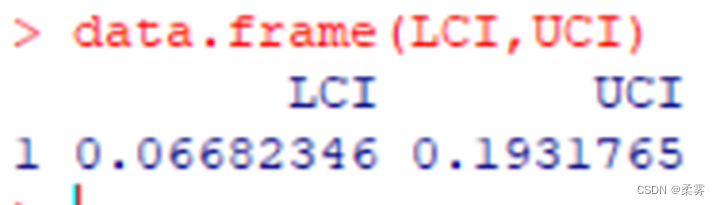
某城市想要进行一项交通措施改革，为征求市民对该项改革措施的意见，在成年人中随机调查了500个市民，其中325人赞成改革措施。用95%的置信水平估计该城市成年人口中赞成该项改革的人数比例的置信区间。
女性与男性收视率差值的95%置信区间(任意大小样本)

n1<-500+2;n2<-400+2
p1<-(225+1)/n1;p2<-(128+1)/n2
q<-qnorm(0.975)
LCI<-p1-p2-q*sqrt(p1*(1-p1)/n1+p2*(1-p2)/n2)
UCI<-p1-p2+q*sqrt(p1*(1-p1)/n1+p2*(1-p2)/n2)
data.frame(LCI,UCI)

练习

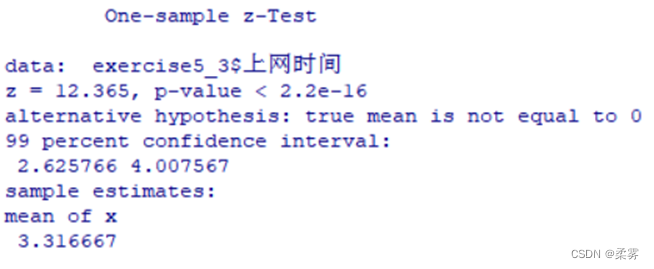
1、某大学为了解学生每天上网的时间，在全校学生中随机抽取36人，调查他们每天上网的时间，得到的数据（单位：小时）如下（exercise5_3.RData）利用函数：

求该校大学生平均上网时间的置信区间，置信水平分别为90%，95%和99%。

load("C:/example/ch5/exercise5_3.RData")
library(BSDA)
z.test(exercise5_3$上网时间,sigma.x=sd(exercise5_3$上网时间),conf.level=0.90)
z.test(exercise5_3$上网时间,sigma.x=sd(exercise5_3$上网时间),conf.level=0.95)
z.test(exercise5_3$上网时间,sigma.x=sd(exercise5_3$上网时间),conf.level=0.99)

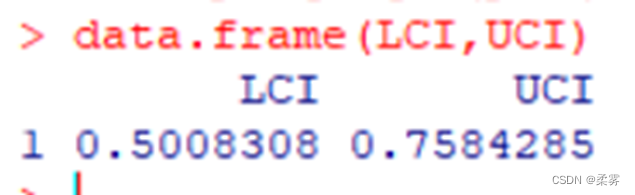
2、某小区共有居民500户，小区管理者准备采取一项新的供水设施，想了解居民是否赞成。
采取重复抽样方法随机抽取50户，其中有32户赞成，18户反对。估计总体中赞成采用新设施的户数比例的置信区间，置信水平为95%（利用公式计算）

n1<-50+4
p1<-(32+2)/n1
q<-qnorm(0.975)
LCI<-p1-q*sqrt(p1*(1-p1)/n1)
UCI<-p1+q*sqrt(p1*(1-p1)/n1)
data.frame(LCI,UCI)

3、顾客到银行办理业务时往往需要等待一些时间，而等待时间的长短与许多因素有关，比如，银行的业务员办理业务的速度、顾客等待排队的方式等等。为此，某银行准备采取两种排队方式进行试验，第一种排队方式是所有顾客都进入一个等待队伍，第二种排队方式是顾客在三个业务窗口处列队三排等待。为比较哪种排队方式使顾客等待的时间更短，银行各随机抽取10名顾客，他们在办理业务时所等待的时间（单位：分钟）如下（exercise5_5.RData利用函数）：


（1）构建第一种排队方式等待时间均值的95%的置信区间

load("C:/example/ch5/exercise5_5.RData")
t.test(exercise5_5$方式1,paired=FALSE,conf.level=0.95)$conf.int

（2）构建两种方式排队时间均值差值的95%的置信区间：

t.test(exercise5_5$方式1,y=exercise5_5$方式2,var.equal=TRUE)$conf.int
t.test(exercise5_5$方式1,y=exercise5_5$方式2,var.equal=FALSE)$conf.int