数据结构与算法（五）

发布时间：2023年12月29日

文章目录

- 数据结构与算法（五）

数据结构与算法（五）

33 与哈希函数有关的结构

内容：
- 哈希函数
- 哈希函数的应用
- 布隆过滤器
- 一致性哈希
- 原理讲述为主，面试只会聊设计，所以本节无题目

33.1 哈希函数

哈希函数作用：可以把数据根据不同值，几乎均匀的分开

public class Hash {
   

	private MessageDigest hash;

	public Hash(String algorithm) {
   
		try {
   
			hash = MessageDigest.getInstance(algorithm);
		} catch (NoSuchAlgorithmException e) {
   
			e.printStackTrace();
		}
	}

	public String hashCode(String input) {
   
		return DatatypeConverter.printHexBinary(hash.digest(input.getBytes())).toUpperCase();
	}

	public static void main(String[] args) {
   
		System.out.println("支持的算法 : ");
		for (String str : Security.getAlgorithms("MessageDigest")) {
   
			System.out.println(str);
		}
		System.out.println("=======");

		String algorithm = "MD5";
		Hash hash = new Hash(algorithm);

		String input1 = "zuochengyunzuochengyun1";
		String input2 = "zuochengyunzuochengyun2";
		String input3 = "zuochengyunzuochengyun3";
		String input4 = "zuochengyunzuochengyun4";
		String input5 = "zuochengyunzuochengyun5";
		System.out.println(hash.hashCode(input1));
		System.out.println(hash.hashCode(input2));
		System.out.println(hash.hashCode(input3));
		System.out.println(hash.hashCode(input4));
		System.out.println(hash.hashCode(input5));
	}
}
支持的算法 : 
SHA-384
SHA-224
SHA-256
MD2
SHA
SHA-512
MD5
=======
B73390C90A49FEF569367FDF894AC89F
451AF105D1062B501663A17F19BA9196
C5A9C27C2BE4EE613311137528AF2D93
E001FC84040DA08AE3B74EB98FD4B468
D0424A6201FD9CB675FC2D40F20DD5D5

33.2 布隆过滤器

利用哈希函数的性质，每一条数据提取特征，加入描黑库。

举例：假设有一个服务，存储了100亿个黑名单的 url。如果用 HashSet 去存，就得需要大概 640G 内存（一个url就是 64 byte，100亿个url就是 6400亿 byte ≈ 640G），及其浪费空间。而使用布隆过滤器可以极大的节省空间，差不多 20G 就可以实现了。但是，布隆过滤器有一定的失误率，这个失误率是针对非黑名单而言的（即：宁可错杀一千，也不可放过一个），并且这个失误率是可控的。

位图：比如 int[10] 可以表示 40 Byte 信息，再比如 bit[n] 可以表示 n/8 Byte 信息。int[10] 就相等于 bit[320]。
假设申请长度为m的bit数组，针对每一个 url，依次经过哈希函数（Hash1、Hash2、…、Hashk）处理后，再模m计算出一个位置并置为1。查询时，通过相同的方式 hashi(url)%m ，得到的位置结果如果全部命中，那么说明该url可能在黑名单中，只要有一个没命中就一定不在黑名单中。
由此可见，问题的关键在于 m 的大小和 hash 函数的个数。

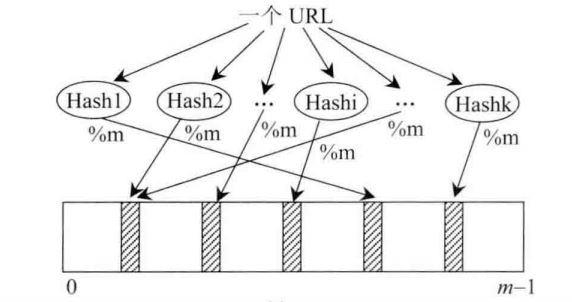
m越大，失误率越小

m 和什么有关？

样本量：100亿

失误率：0.01%

~~单样本大小：64 byte（和这个无关）~~

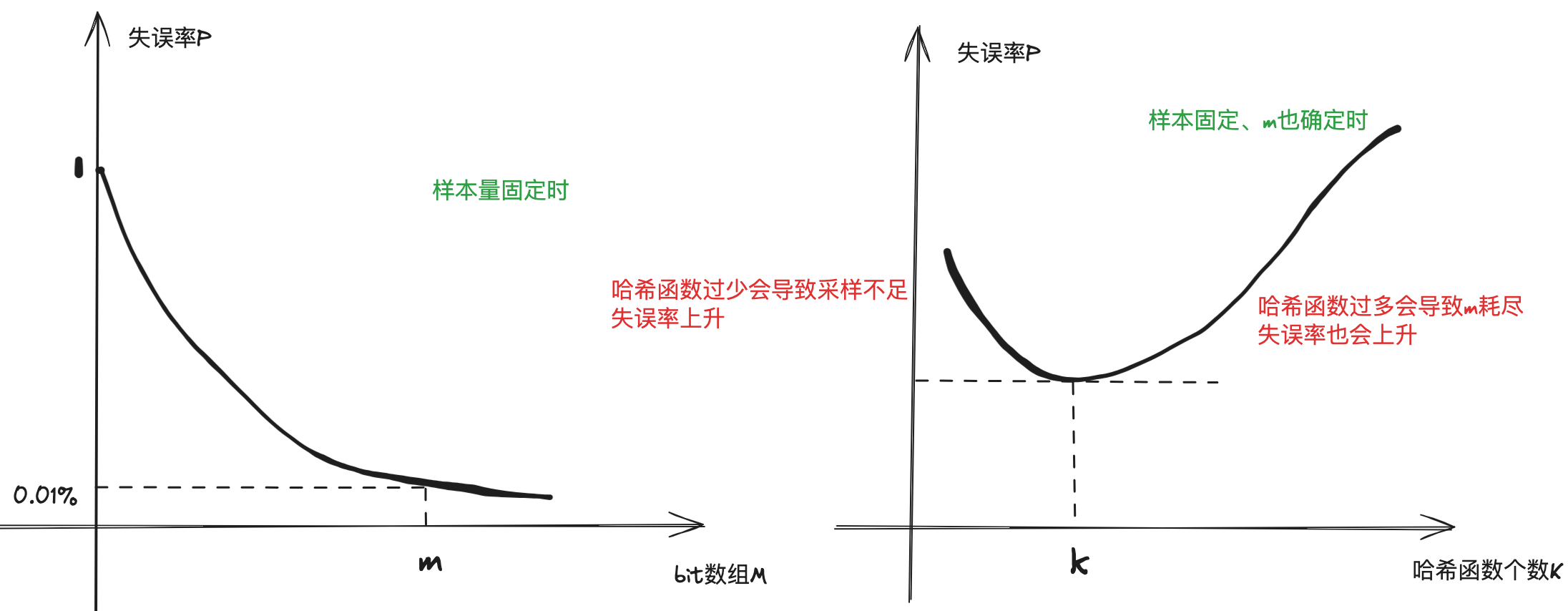
布隆过滤器重要的三个公式：

以上三个公式需要背一下。
- ① 根据确定的样本量 n 和预期的失误率 p，由第一个公式计算出一个m，对m向上取整得到一个实际的 m’；
- ② 将 m’ 带入到第二个公式计算出一个k，对k向上取整得到一个实际的 k’；
- ③ 将 m’ 和 k’ 带入到第三个公式计算出一个真实的失误率 p’，这个值一定小于 p。

接下来的问题是，如果需要 k 多个哈希函数，怎么来？

只需要有两个哈希函数（f1、f2）就可以造出 k 个哈希函数，而且几乎都是独立的。
- ① 1*f1() + f2
- ② 2*f1() + f2
- ③ 3*f1() + f2
- …
布隆过滤器的应用-HDFS
http://www.bubuko.com/infodetail-3803533.html

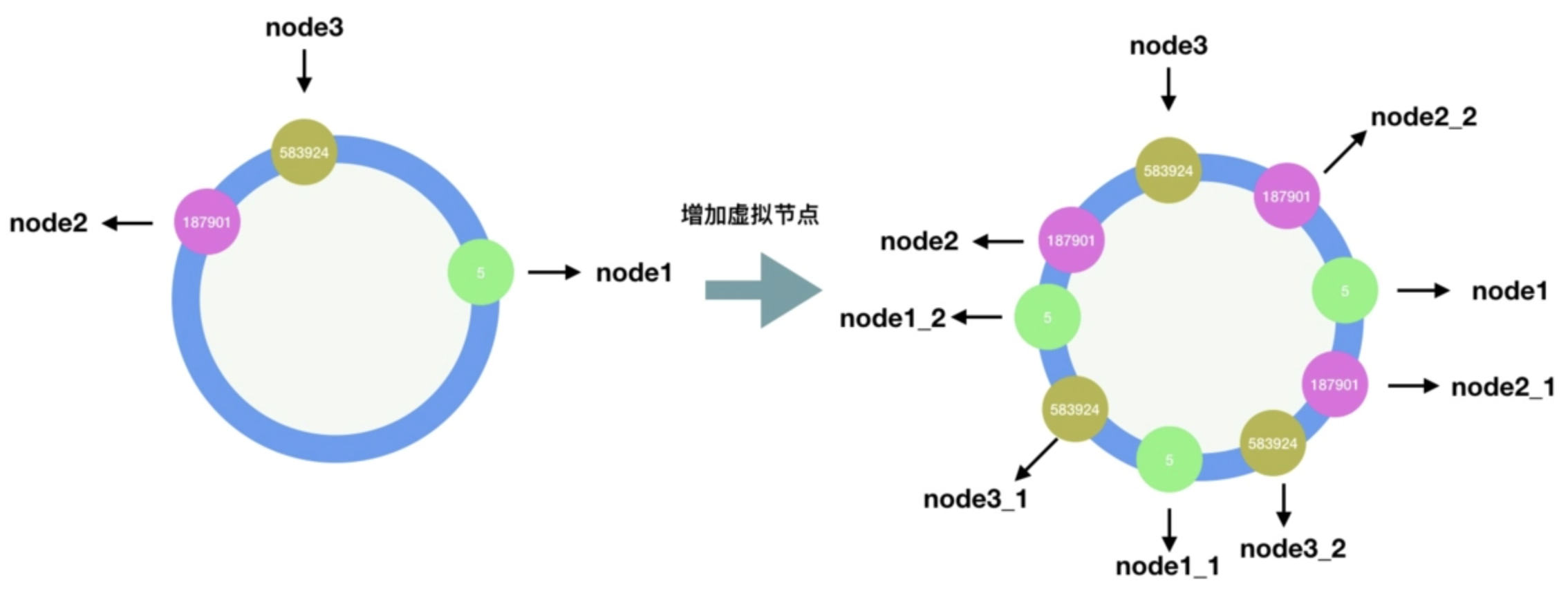
33.3 一致性哈希

分布式存储结构最常见的结构
- 哈希域成环的设计
- 虚拟节点技术：既可以解决负载均衡，也可以实现负载管理（调整虚拟节点的个数）

34 资源限制类题目的解题套路

内容：
- 布隆过滤器用于集合的建立与查询，并可以节省大量空间（33讲）
- 一致性哈希解决数据服务器的负载管理问题（33讲）
- 利用并查集结构做岛问题的并行计算（14讲）
- 哈希函数可以把数据按照种类均匀分流
- 位图解决某一范围上数字的出现情况，并可以节省大量空间
- 利用分段统计思想、并进一步节省大量空间
- 利用堆、外排序来做多个处理单元的结果合并

34.1 1G内存40亿个无符号整数的文件中找到出现次数最多的数

32位无符号整数的范围是0~4,294,967,295，现在有一个正好包含40亿个无符号整数的文件，可以使用最多1GB的内存，怎么找到出现次数最多的数？

如果将这 40 亿个数进行排序，内存空间至少需要 40亿 * 4Byte = 16 GB > 1GB，不可行；
如果直接用 HashMap 进行词频统计，最坏情况下（所有数字都不同）内存空间至少需要 40亿 * 4Byte * 4Byte = 32GB > 1GB，也不可行；
所有，我们反过来想，1GB 内存如果用 HashMap 最多可以存多少种不同的数字？答案是 1GB / 8 = 1.25 亿，然后我们保守一点（考虑一些其他的内存开销），比如只存1千万种数。那么我们可以将这个大文件分成 40亿 / 1千万 = 400 个小文件，然后循环利用这 1GB 内存分别得到这 400 个小文件中出现次数最多的数，并从这400个数中求一个最大值。
- 怎么将这个 40 亿个数均匀分到这 400 个小文件？这里就用到了哈希函数，即对每个数利用哈希函数计算后，模 400 后写入到对应的文件中。

34.2 内存限制为3KB，但是只用找到一个没出现过的数

32位无符号整数的范围是0~4,294,967,295，现在有一个正好包含40亿个无符号整数的文件，所以在整个范围中必然存在没出现过的数，可以使用最多1GB的内存，怎么找到所有未出现过的数？

如果直接用 HashSet 存这 40 亿个数，内存空间最少需要 40亿 * 4Byte = 16GB > 1GB，不可行；
可以利用位图 bit[] 数组，某一bit位为1表示出现过，0表示没出现过，那么最坏情况 40 亿个数都不同，需要的内存空间是 40亿/8 Byte = 500 MB < 1GB，这种方式可行。
- 也可以利用整型数组 int[]来存，int[0] 表示 0~31位、int[1] 表示 32~63位、int[2] 表示 64~95位，针对每个数 x 先计算 x/32 定位到整型数组的位置 i，然后 x%32 定位到 int[i] 中具体第几位，置为1；
- 那么所有为 0 的位置就都是没有出现过的数。

进阶：内存限制为3KB，但是只用找到一个没出现过的数即可

如果 3KB 都用来存 int[] arr数组，得有多长？3000 / 4 = 750，然后长度取 512 < 750最近的 2 的某次方。
接下来，将32位无符号整数（2^32）均分成 512 份，那么每一份负责的数有 2^32 / 512 = 2^23 = 8388608 个，即 arr[0] 统计 0~8388607、arr[1] 统计 8388608~16777215、arr[2] 统计 16777216~25165823、…
- 从中找到统计不满的（不全是1的），利用同样的方式除以 512，均分成 512 份，即即 arr[0] 统计 0~16383、arr[1] 统计 16384~32767、arr[2] 统计 32768~49152、…
- 这样，经过有限的几轮就能定位到一个没出现过的数。
这就是 512 分法

再次升级：用有限几个变量，找到一个没出现过的数

二分法：首先 L = 0、R = (2^32)-1、mid = (L+R)/2，分别统计左右两侧出现过的数有几个，如果那侧不够 2^31 个数，就二分递归下去，最后总能定位到这个没出现过的数。

34.3 100亿个URL的大文件中找出其中所有重复的URL

有一个包含100亿个URL的大文件，假设每个URL占用64B，请找出其中所有重复的URL。
补充：某搜索公司一天的用户搜索词汇是海量的(百亿数据量)，请设计一种求出每天热门Top100词汇的可行办法

如果允许有失误率，可以使用布隆过滤器
如果不允许有失误率，可以使用哈希分流的思想

34.4 40亿个无符号整数找出所有出现了两次的数

32位无符号整数的范围是0~4294967295，现在有40亿个无符号整数，可以使用最多1GB的内存，找出所有出现了两次的数

用两个 bit 位表示一个数字出现了几次：00 出现0次、01 出现1次、10 出现2次、11 出现3次及以上
40 亿个数需要内存空间 = 40亿 * 2bit = 80亿bit = 10亿Byte = 1GB 刚好够
如果担心内存不够，就用分段统计

34.5 40亿个无符号整数的中位数

32位无符号整数的范围是0~4294967295，现在有40亿个无符号整数，可以使用最多3K的内存，怎么找到这40亿个整数的中位数？

申请一个长度512的整型数组 int[] arr，将32位无符号整数均分成 512 份，arr[0] 统计 0~8388607、arr[1] 统计 8388608~16777215、arr[2] 统计 16777216~25165823、…。然后依次累加每一份出现的数个数，假设到 arr[170] 时已经总共有 19 亿个数了，arr[171] 有 2 亿数，接下来找到 arr[171] 中第 1 亿小的数（刚好第20亿个数）就是所求中位数。

34.6 对一个10G大小的文件中的数字排序

32位无符号整数的范围是0~4294967295，有一个10G大小的文件，每一行都装着这种类型的数字，整个文件是无序的，给你5G的内存空间，请你输出一个10G大小的文件，就是原文件所有数字排序的结果。

利用堆结构，堆中元素是每个数出现的词频<k,v>，5G内存空间最多可以存 5G/(4+8)Byte ≈ 4.1亿个数，担心内存不够，就保守一点按 4000万个数来算。每次读入10G文件，利用堆得到前 4000万的数，然后从小到大依次写入文件，并记下第 4000万大的数；下一次读入10G文件时，遇到小于第 4000万大的数直接跳过，收集第 4000万大数之后的 4000万个数，再从小到大依次写入文件，再记下这一次第 4000万大的数；依此循环往复，直到凑不齐 4000万个数，结束循环，将剩下的数从小到大依次写入文件。

35 有序表（上）

内容：
- 平衡搜索二叉树：对于任意节点，左右子树的高度差不大于1
- 左旋
- 右旋
- AVL树的节点违规4种类型（LL，LR，RL，RR）

35.1 平衡二叉树的插入与删除

插入：10 和根节点 20 比较 ==>> 10 和 17 比较 ==>> 10 和 3 比较 ==>> 插入到 3 节点的右子树

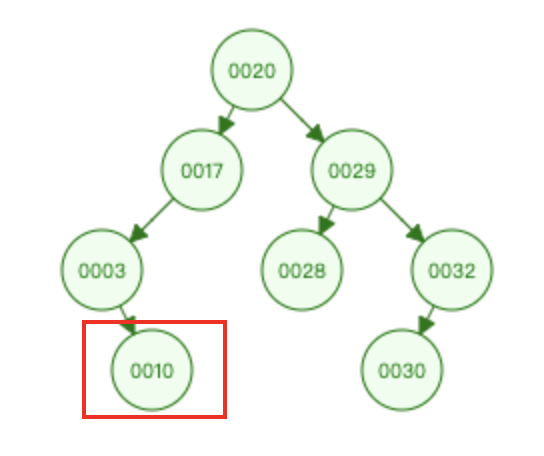
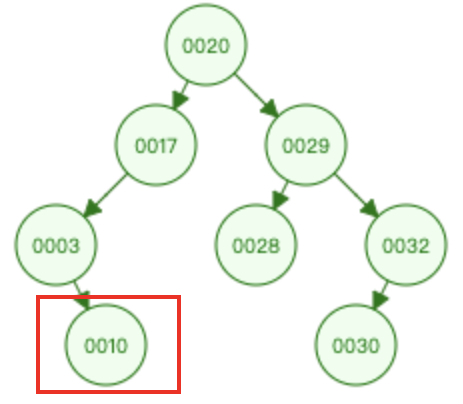
删除：
- 叶子节点：10、28、30 直接删除
- 删除出度为1的节点：3、17、32 提升 3 的唯一子树
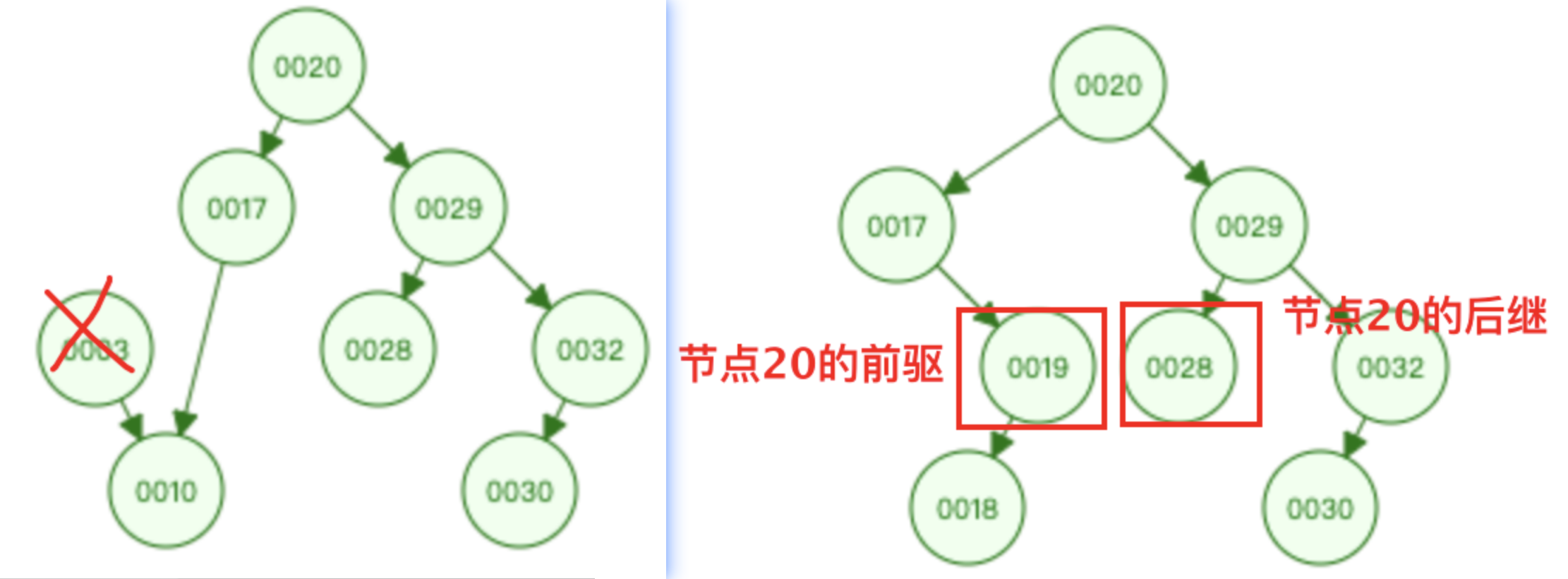
- 删除出度为2的节点：20、29 找到前驱或者后继节点进行替换，替换后转换为删除度为1或度为0的问题

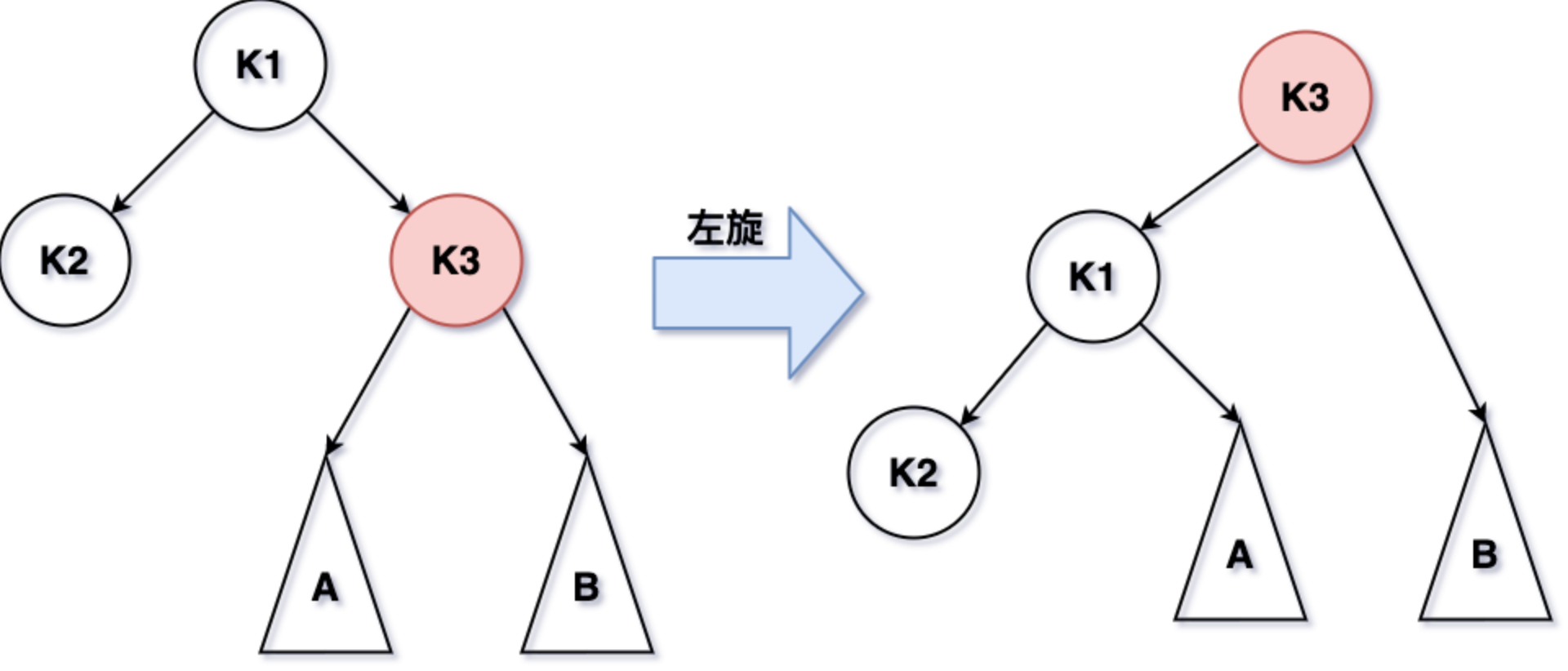
35.2 AVL树的左旋与右旋

左旋

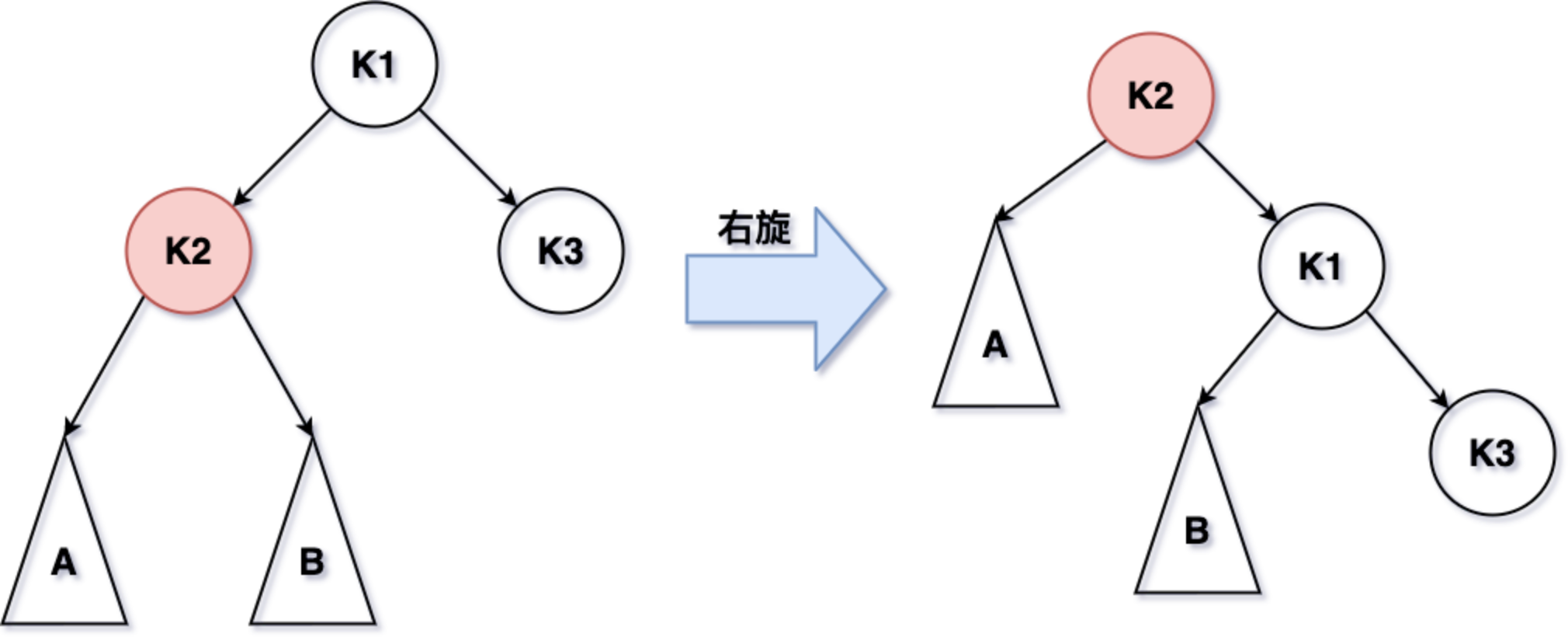
右旋

失衡类型：

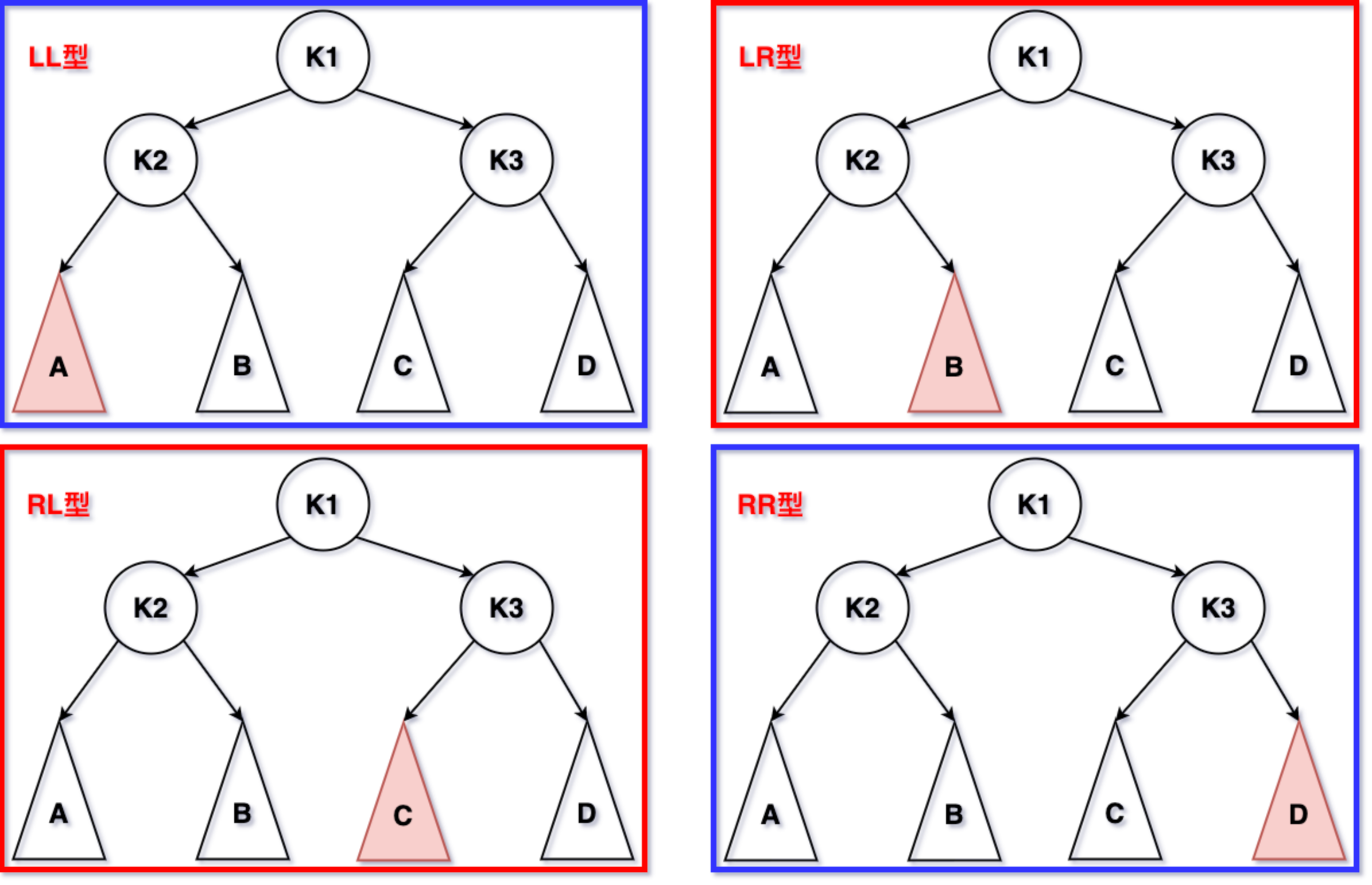
LL型的失衡调整：对根节点进行一次大右旋即可；
RR型的失衡调整：对根节点进行一次大左旋即可；
LR型的失衡调整：先左子树进行一次小左旋，再根节点进行一次大右旋即可；
RL型的失衡调整：先右子树进行一次小右旋，再根节点进行一次大左旋即可；
LL+LR失衡：按LL失衡调整；
RR+RL失衡：按RR失衡调整；
不可能出现 LL+RR失衡。

35.3 AVL树的实现

public static class AVLNode<K extends Comparable<K>, V> {
   
	public K k;
	public V v;
	public AVLNode<K, V> l;
	public AVLNode<K, V> r;
	public int h;

	public AVLNode(K key, V value) {
   
		k = key;
		v = value;
		h = 1;
	}
}

public static class AVLTreeMap<K extends Comparable<K>, V> {
   
	private AVLNode<K, V> root;
	private int size;

	public AVLTreeMap() {
   
		root = null;
		size = 0;
	}

	private AVLNode<K, V> rightRotate(AVLNode<K, V> cur) {
   
		AVLNode<K, V> left = cur.l;
		cur.l = left.r;
		left.r = cur;
		cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;
		left.h = Math.max((left.l != null ? left.l.h : 0), left.r.h) + 1;
		return left;
	}

	private AVLNode<K, V> leftRotate(AVLNode<K, V> cur) {
   
		AVLNode<K, V> right = cur.r;
		cur.r = right.l;
		right.l = cur;
		cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;
		right.h = Math.max(right.l.h, (right.r != null ? right.r.h : 0)) + 1;
		return right;
	}

	private AVLNode<K, V> rebalance(AVLNode<K, V> cur) {
   
		if (cur == null) return null;
		int leftHeight = cur.l != null ? cur.l.h : 0;
		int rightHeight = cur.r != null ? cur.r.h : 0;
		if (Math.abs(leftHeight - rightHeight) <= 1) return cur;
		if (leftHeight > rightHeight) {
   
			int leftLeftHeight = cur.l != null && cur.l.l != null ? cur.l.l.h : 0;
			int leftRightHeight = cur.l != null && cur.l.r != null ? cur.l.r.h : 0;
			if (leftLeftHeight >= leftRightHeight) {
   
				return rightRotate(cur);
			} else {
   
				cur.l = leftRotate(cur.l);
				return rightRotate(cur);
			}
		} else {
   
			int rightLeftHeight = cur.r != null && cur.r.l != null ? cur.r.l.h : 0;
			int rightRightHeight = cur.r != null && cur.r.r != null ? cur.r.r.h : 0;
			if (rightRightHeight >= rightLeftHeight) {
   
				return leftRotate(cur);
			} else {
   
				cur.r = rightRotate(cur.r);
				return leftRotate(cur);
			}
		}
	}

	private AVLNode<K, V> findLastIndex(K key) {
   
		AVLNode<K, V> pre = root;
		AVLNode<K, V> cur = root;
		while (cur != null) {
   
			pre = cur;
			if (key.compareTo(cur.k) == 0) {
   
				break;
			} else if (key.compareTo(cur.k) < 0) {
   
				cur = cur.l;
			} else {
   
				cur = cur.r;
			}
		}
		return pre;
	}

	private AVLNode<K, V> findLastNoSmallIndex(K key) {
   
		AVLNode<K, V> ans = null;
		AVLNode<K, V> cur = root;
		while (cur != null) {
   
			if (key.compareTo(cur.k) == 0) {
   
				ans = cur;
				break;
			} else if (key.compareTo(cur.k) < 0) {
   
				ans = cur;
				cur = cur.l;
			} else {
   
				cur = cur.r;
			}
		}
		return ans;
	}

	private AVLNode<K, V> findLastNoBigIndex(K key) {
   
		AVLNode<K, V> ans = null;
		AVLNode<K, V> cur = root;
		while (cur != null) {
   
			if (key.compareTo(cur.k) == 0) {
   
				ans = cur;
				break;
			} else if (key.compareTo(cur.k) < 0) {
   
				cur = cur.l;
			} else {
   
				ans = cur;
				cur = cur.r;
			}
		}
		return ans;
	}

	private AVLNode<K, V> add(AVLNode<K, V> cur, K key, V value) {
   
		if (cur == null) return new AVLNode<>(key, value);

		if (key.compareTo(cur.k) < 0) {
   
			cur.l = add(cur.l, key, value);
		} else {
   
			cur.r = add(cur.r, key, value);
		}
		cur.h = Math.max(cur.l != null ? cur.l.h : 0, cur.r != null ? cur.r.h : 0) + 1;
		return rebalance(cur);
	}

	// 在cur这棵树上，删掉key所代表的节点
	// 返回cur这棵树的新头部
	private AVLNode<K, V> delete(AVLNode<K, V> cur, K key) {
   
		if (key.compareTo(cur.k) > 0) {
   
			cur.r = delete(cur.r, key);
		} else if (key.compareTo(cur.k) < 0) {
   
			cur.l = delete(cur.l, key);
		} else {
   
			if (cur.l == null && cur.r == null) {
   
				cur = null;
			} else if (cur.l == null) {
   
				cur = cur.r;
			} else if (cur.r == null) {
   
				cur = cur.l;
			} else {
   
				AVLNode<K, V> des = cur.r;
				while (des.l != null) {
   
					des = des.l;
				}
				cur.r = delete(cur.r, des.k);
				des.l = cur.l;
				des.r = cur.r;
				cur = des;
			}
		}
		if (cur != null) {
   
			cur.h = Math.max(cur.l != null ? cur.l.h : 0, cur.r != null ? cur.r.h : 0) + 1;
		}
		return rebalance(cur);
	}

	public int size() {
   
		return size;
	}

	public boolean containsKey(K key) {
   
		if (key == null) {
   
			return false;
		}
		AVLNode<K, V> lastNode = findLastIndex(key);
		return lastNode != null && key.compareTo(lastNode.k) == 0;
	}

	public void put(K key, V value) {
   
		if (key == null) {
   
			return;
		}
		AVLNode<K, V> lastNode = findLastIndex(key);
		if (lastNode != null && key.compareTo(lastNode.k) == 0) {
   
			lastNode.v = value;
		} else {
   
			size++;
			root = add(root, key, value);
		}
	}

	public void remove(K key) {
   
		if (key == null) {
   
			return;
		}
		if (containsKey(key)) {
   
			size--;
			root = delete(root, key);
		}
	}

	public V get(K key) {
   
		if (key == null) {
   
			return null;
		}
		AVLNode<K, V> lastNode = findLastIndex(key);
		if (lastNode != null && key.compareTo(lastNode.k) == 0) {
   
			return lastNode.v;
		}
		return null;
	}

	public K firstKey() {
   
		if (root == null) {
   
			return null;
		}
		AVLNode<K, V> cur = root;
		while (cur.l != null) {
   
			cur = cur.l;
		}
		return cur.k;
	}

	public K lastKey() {
   
		if (root == null) {
   
			return null;
		}
		AVLNode<K, V> cur = root;
		while (cur.r != null) {
   
			cur = cur.r;
		}
		return cur.k;
	}

	public K floorKey(K key) {
   
		if (key == null) {
   
			return null;
		}
		AVLNode<K, V> lastNoBigNode = findLastNoBigIndex(key);
		return lastNoBigNode == null ? null : lastNoBigNode.k;
	}

	public K ceilingKey(K key) {
   
		if (key == null) {
   
			return null;
		}
		AVLNode<K, V> lastNoSmallNode = findLastNoSmallIndex(key);
		return lastNoSmallNode == null ? null : lastNoSmallNode.k;
	}
}

36 有序表（中）

内容：
- size-balanced-tree：对于任意节点，其叔叔节点的子树节点个数不能少于当前节点个数。也有4种失衡类型，也需要进行左旋和右旋调整，除此之外对于受影响的节点会依次递归调整
  - LL失衡
  - LR失衡
  - RL失衡
  - RR失衡
- skiplist详解
- 聊聊红黑树

36.1 size-balanced-tree实现

public static class SBTNode<K extends Comparable<K>, V> {
   
	public K key;
	public V value;
	public SBTNode<K, V> l;
	public SBTNode<K, V> r;
	public int size; // 不同的key的数量

	public SBTNode(K key, V value) {
   
		this.key = key;
		this.value = value;
		size = 1;
	}
}

public static class SizeBalancedTreeMap<K extends Comparable<K>, V> {
   
	private SBTNode<K, V> root;

	private SBTNode<K, V> rightRotate(SBTNode<K, V> cur) {
   
		SBTNode<K, V> leftNode = cur.l;
		cur.l = leftNode.r;
		leftNode.r = cur;
		// 区别于AVL树，这里是互换size
		leftNode.size = cur.size;
		cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
		return leftNode;
	}

	private SBTNode<K, V> leftRotate(SBTNode<K, V> cur) {
   
		SBTNode<K, V> rightNode = cur.r;
		cur.r = rightNode.l;
		rightNode.l = cur;
		// 区别于AVL树，这里是互换size
		rightNode.size = cur.size;
		cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;
		return rightNode;
	}

	private SBTNode<K, V> reBalance(SBTNode<K, V> cur) {
   
		if (cur == null) return null;
		int leftSize = cur.l != null ? cur.l.size : 0;
		int leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;
		int leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;
		int rightSize = cur.r != null ? cur.r.size : 0;
		int rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;
		int rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;
		if (leftLeftSize > rightSize) {
    // LL
			cur = rightRotate(cur);
			cur.r = reBalance(cur.r);
			cur = reBalance(cur);
		} else if (leftRightSize > rightSize) {
    // LR
			cur.l = leftRotate(cur.l);
			cur = rightRotate(cur);
			cur.l = reBalance(cur.l);
			cur.r = reBalance(cur.r);
			cur = reBalance(cur);
		} else if (rightRightSize > leftSize) {
    // RR
			cur = leftRotate(cur);
			cur.l = reBalance(cur.l);
			cur = reBalance(cur);
		} else if (rightLeftSize > leftSize) {
    // RR
			cur.r = rightRotate(cur.r);
			cur = leftRotate(cur);
			cur.l = reBalance(cur.l);
			cur.r = reBalance(cur.r);
			cur = reBalance(cur);
		}
		return cur;
	}

	private SBTNode<K, V> findLastIndex(K key) {
   
		SBTNode<K, V> pre = root;
		SBTNode<K, V> cur = root;
		while (cur != null) {
   
			pre = cur;
			if (key.compareTo(cur.key) == 0) {
   
				break;
			} else if (key.compareTo(cur.key) < 0) {
   
				cur = cur.l;
			} else {
   
				cur = cur.r

文章来源:https://blog.csdn.net/yangwei234/article/details/135295754
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！