八种无监督聚类算法说明
?目录
?三、?Agglomerative Clustering (Hierarchical) -- Connectivity models
无监督聚类是一种机器学习技术,用于将数据分组成不同的类别,而无需提前标记或指导。在无监督聚类中,算法通过分析数据之间的相似性和差异性,自动将数据划分为具有相似特征的组。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn.cluster as cluster
import time
%matplotlib inline
data = np.load('clusterable_data.npy')#这是一个类似细胞的数据集
plt.scatter(data.T[0], data.T[1], c='b')
frame = plt.gca()
frame.axes.get_xaxis().set_visible(False)
frame.axes.get_yaxis().set_visible(False)

一、前四种聚类方法四种无监督聚类算法说明-CSDN博客
?二、Spectral Clustering
Spectral Clustering是一种基于谱图理论的聚类算法,它将数据集投影到低维空间,并在该空间中执行聚类。
Spectral Clustering的基本思想是将数据集看作是一个图,其中每个数据点表示图中的一个节点,而数据点之间的相似性信息则表示图中边的权重。根据这个图可以构建一个拉普拉斯矩阵,通过对该矩阵进行特征分解,可以得到数据集在低维空间中的表示。然后,可以应用传统的聚类算法,如k-means,来对低维空间中的数据进行聚类。
Spectral Clustering的优势在于它可以处理非线性的数据集,并且对于复杂的聚类结构有很好的适应性。它不仅可以分割凸型聚类结构,还可以将环形聚类、嵌套聚类等非凸型结构分割出来。此外,Spectral Clustering还可以处理高维数据集,并且对噪音和异常值具有一定的鲁棒性。
然而,Spectral Clustering也有一些缺点。首先,它的计算复杂度较高,特别是在处理大规模数据集时。其次,Spectral Clustering通常需要事先确定聚类的个数,这对于一些实际应用中并不容易确定。此外,Spectral Clustering对参数的选择比较敏感,如果选择不当,可能会导致聚类结果不理想。
#Spectral Clustering
from numpy import unique
from sklearn.cluster import SpectralClustering
from matplotlib import pyplot
# define the model
model = SpectralClustering(n_clusters=6)
# fit model and predict clusters
yhat = model.fit_predict(data)
# retrieve unique clusters
clusters = unique(yhat)
palette = sns.color_palette('deep', np.unique(yhat).max() + 1)
colors = [palette[x] if x >= 0 else (0.0, 0.0, 0.0) for x in yhat]
plt.scatter(data.T[0], data.T[1], c=colors)
frame = plt.gca()
frame.axes.get_xaxis().set_visible(False)
frame.axes.get_yaxis().set_visible(False)
plt.title('Clusters found by Spectral Clustering')
clusters
#array([0, 1, 2, 3, 4, 5])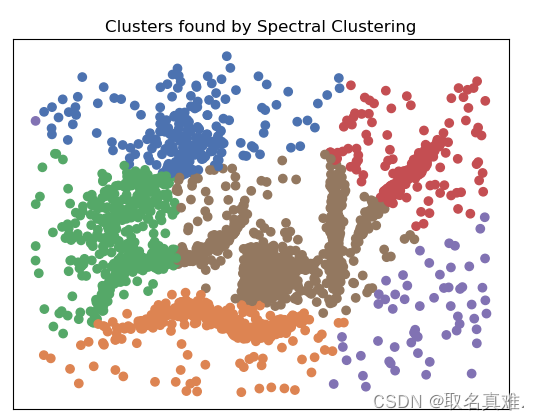
?三、?Agglomerative Clustering (Hierarchical) -- Connectivity models
AgglomerativeClustering是一种层次聚类算法,也被称为自底向上聚类。该算法将每个数据点视为一个单独的簇,然后通过计算相似度,将最相似的簇合并成更大的簇,直到所有的数据点都被合并为一个簇或达到预设的簇个数。
AgglomerativeClustering的聚类过程如下:
- 将每个数据点看作一个簇。
- 计算所有簇之间的相似度或距离。
- 选择相似度或距离最小的簇对,并将它们合并成一个新的簇。
- 更新相似度矩阵或距离矩阵,计算新的簇与其他簇之间的相似度或距离。
- 重复步骤3和4,直到达到预设的簇个数或只剩下一个簇。
AgglomerativeClustering的优点是可以处理任意形状的簇,且不需要预先指定簇的个数。然而,该算法的计算复杂度较高,特别是当数据点较多时,计算时间会相对较长。
AgglomerativeClustering函数的linkage参数类型(含义):
ward、complete、average和single是聚合策略,用于指定在执行层次聚类时如何计算样本之间的距离。这些策略会导致不同的聚类结果。
1. "ward":使用Ward方差最小化算法,该算法会尽量将每个簇内样本的方差最小化。该策略通常是默认策略,它在大多数情况下都能产生较好的聚类效果。
2. "complete":使用最远邻距离作为样本间的距离。它计算两个簇中样本之间的最大距离,然后将这两个簇合并为一个簇。
3. "average":使用平均距离作为样本间的距离。它计算两个簇中样本之间的平均距离,然后将这两个簇合并为一个簇。
4. "single":使用最近邻距离作为样本间的距离。它计算两个簇中样本之间的最小距离,然后将这两个簇合并为一个簇。
这些聚合策略在层次聚类过程中会根据样本之间的距离来选择合适的簇进行合并,最终形成聚类结果。具体选择哪个策略取决于数据的特性和聚类的目的。
#Ward (Hierarchical) -- Connectivity models
# Agglomerative Clustering (Hierarchical) -- Connectivity models
# Agglomerative Clustering/Ward clustering
from numpy import unique
from sklearn.cluster import AgglomerativeClustering
from matplotlib import pyplot
# define the model
model = AgglomerativeClustering(n_clusters=6,linkage='ward')
# fit model and predict clusters
yhat = model.fit_predict(data)
# retrieve unique clusters
clusters = unique(yhat)
palette = sns.color_palette('deep', np.unique(yhat).max() + 1)
colors = [palette[x] if x >= 0 else (0.0, 0.0, 0.0) for x in yhat]
plt.scatter(data.T[0], data.T[1], c=colors)
frame = plt.gca()
frame.axes.get_xaxis().set_visible(False)
frame.axes.get_yaxis().set_visible(False)
plt.title('Clusters found by Agglomerative Clustering')
clusters
#结果:array([0, 1, 2, 3, 4, 5], dtype=int64)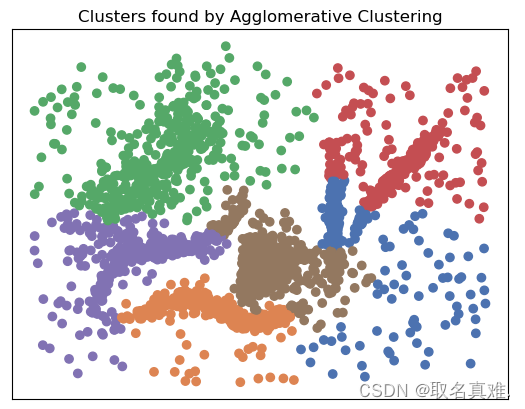
四、?DBSCAN
DBSCAN是一种密度聚类算法,全称为Density-Based Spatial Clustering of Applications with Noise。它通过基于数据点之间的密度来进行聚类,不需要预先指定聚类的数量。DBSCAN算法将数据点分为核心点、边界点和噪声点。
DBSCAN的工作原理如下:
- 选择一个未被访问的数据点,检查它的邻域内的数据点数量。
- 如果该点的邻域内的数据点数量大于等于指定的密度阈值(MinPts),将该点标记为核心点,并将其邻域内的点加入到该簇中。
- 对于邻域内的每个点,如果该点也是核心点,那么将其邻域内的点加入到该簇中。
- 重复步骤2和步骤3,将所有可以被访问的点都划分到一个簇中。
- 如果一个点的邻域内的数据点数量小于MinPts,则将该点标记为边界点。
- 如果一个点既不是核心点也不是边界点,则将其标记为噪声点。
DBSCAN的优点是可以发现任意形状的聚类,对噪声点有较好的容忍性。它不需要预先指定聚类的数量,并且对参数的选择相对较少。然而,DBSCAN算法对于高维数据和不同密度之间的聚类效果可能不佳,而且对参数的选择敏感。
from numpy import unique
from sklearn.cluster import DBSCAN
from matplotlib import pyplot
# define the model
model = DBSCAN(eps=0.025)
# fit model and predict clusters
yhat = model.fit_predict(data)
# retrieve unique clusters
clusters = unique(yhat)
palette = sns.color_palette('deep', np.unique(yhat).max() + 1)
colors = [palette[x] if x >= 0 else (0.0, 0.0, 0.0) for x in yhat]
plt.scatter(data.T[0], data.T[1], c=colors)
frame = plt.gca()
frame.axes.get_xaxis().set_visible(False)
frame.axes.get_yaxis().set_visible(False)
plt.title('Clusters found by DBSCAN')
clusters
#结果:array([-1, 0, 1, 2, 3, 4, 5, 6, 7], dtype=int64) -1是噪音,即图上黑点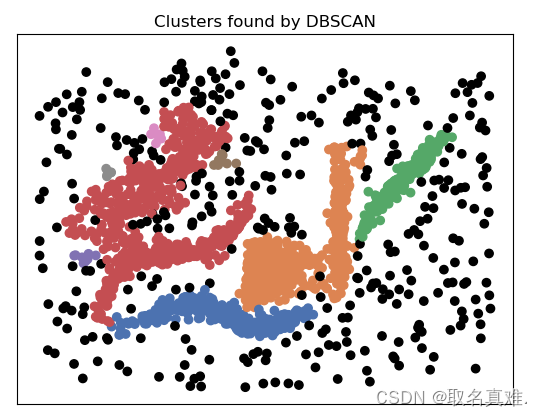
五、BIRCH?
BIRCH(Balanced Iterative Reducing and Clustering using Hierarchies)是一种层次聚类算法。它通过一种层次化的方式对大规模数据进行聚类,能够有效地处理大量数据并减少聚类时间和内存消耗。
BIRCH算法的工作原理如下:
- 通过构建一棵CF树(Clustering Feature Tree)来表示数据集。CF树是一种高效的层次聚类结构,其节点包含聚类中心与代表性特征。通过逐步聚合数据点,构建出一棵平衡的CF树。
- 在构建CF树的过程中,使用一种紧凑的数据结构来存储数据点,称为CF(Clustering Feature)。CF通过统计每个聚类的数据点数量、平均值、协方差等信息来代表聚类。
- 在查询阶段,可以使用CF树来快速找到与查询点最近的聚类中心。通过沿着CF树搜索,逐级将查询点与子聚类进行比较,最终找到最合适的聚类中心。
- 根据需要,可以使用层次聚类方法从CF树中提取出最终的聚类结果。
BIRCH算法的特点是在构建CF树和查询过程中的时间复杂度低,适用于处理大规模数据,并且可以在一次遍历数据集的情况下进行聚类。然而,BIRCH算法对数据的分布假设较强,对于非凸形状的聚类效果可能不佳。
from numpy import unique
from sklearn.cluster import Birch
from matplotlib import pyplot
# define the model
model = Birch(threshold=0.01, n_clusters=6)
# fit model and predict clusters
yhat = model.fit_predict(data)
# retrieve unique clusters
clusters = unique(yhat)
palette = sns.color_palette('deep', np.unique(yhat).max() + 1)
colors = [palette[x] if x >= 0 else (0.0, 0.0, 0.0) for x in yhat]
plt.scatter(data.T[0], data.T[1], c=colors)
frame = plt.gca()
frame.axes.get_xaxis().set_visible(False)
frame.axes.get_yaxis().set_visible(False)
plt.title('Clusters found by Birch')
clusters
#结果:array([0, 1, 2, 3, 4, 5], dtype=int64)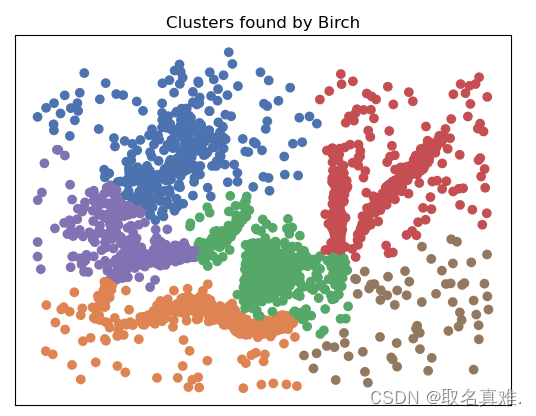
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 【Leetcode】74. 搜索二维矩阵
- 100天精通Python(实用脚本篇)——第113天:基于Tesseract-OCR实现OCR图片文字识别实战
- Redis 服务器 命令
- 瑞金市城北社区开展新时代文明实践文艺汇演
- feign项目中使用
- jmeter自动录制脚本功能
- IP属地变化背后的原因
- MySQL5.7服务器系统变量(一)
- Packet Tracer - Configuring Extended ACLs - Scenario 1
- 如何衡量一个排序算法的性能