【MATLAB第84期】基于MATLAB的波形叠加极限学习机SW-ELM代理模型的sobol全局敏感性分析法应用

【MATLAB第84期】基于MATLAB的波形叠加极限学习机SW-ELM代理模型的sobol全局敏感性分析法应用

前言

跟往期sobol区别：
1.sobol计算依赖于验证集样本，无需定义变量上下限。
2.SW-ELM自带激活函数，计算具有phi（x）=e^x激活函数的单层神经网络的一阶和总Sobol指数
本篇文章将演示如何实现波形叠加极限学习机SW-ELM来计算示例模型的一阶和总Sobol指数。

共有四个部分：
1.生成训练和验证集
2.构建ELM的参数。要使用多少个基函数？使用什么正则化参数？要测试哪些稀疏化参数？
3.SW-ELM代理构建并执行全局敏感性分析
4.绘图

一、生成训练和验证集

clear all
res = xlsread('数据集.xlsx');

%%  划分训练集和测试集
%temp = randperm(103);
temp=1:103
P_train = res(temp(1: 80), 1: 7)';
T_train = res(temp(1: 80), 8)';
M = size(P_train, 2);

P_test = res(temp(81: end), 1: 7)';
T_test = res(temp(81: end), 8)';
N = size(P_test, 2);

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);

%%  转置以适应模型
p_train = p_train'; p_test = p_test';
t_train = t_train'; t_test = t_test';

二、ELM参数设置

model_data.nneurons=500;%隐藏层神经元的数量，即ELM基函数
model_data.lambda=1e-4;%L2正则化参数
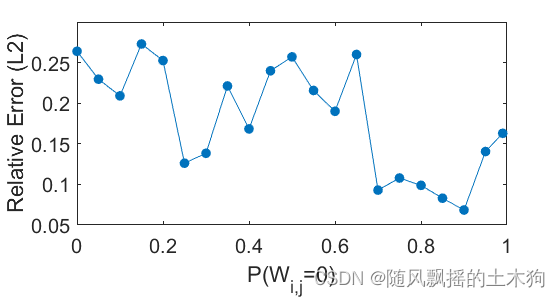
p_list=[0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8 0.85 0.9 0.95 0.99];%这里列出了所有要测试的稀疏化参数。
p_sz = length(p_list); %要测试的稀疏化参数的数量

ndim = size(p_train,2); %输入维度
s_sz = size(p_train,1);%训练集大小
Xd_train = p_train; Yd_train = t_train;

va_sz = size(p_test,1); % 验证集数量
Xd_valid = p_test; Yd_valid = t_test;

三、SW-ELM代理构建并执行全局敏感性分析

 elm_valid = exp(Xd_valid * W + bias) * beta;
rel(j) = rel(j) + norm(Yd_valid - elm_valid) / norm(Yd_valid); %选择哪一个稀疏化参数最好的相对误差估计
[W,bias,beta] = ELM(Xd_train,Yd_train,model_data);
elm_valid = exp(Xd_valid * W + bias) * beta; 
T_sim2 = mapminmax('reverse', elm_valid, ps_output);
error = norm(T_test' - T_sim2) / norm(T_test'); % SW-ELM误差
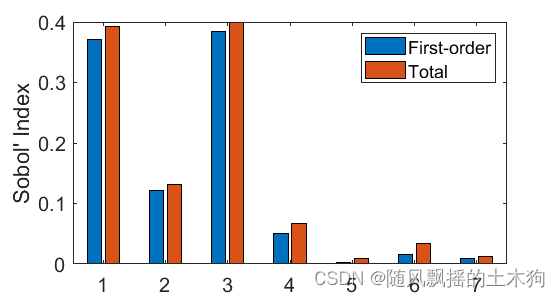
[sobolR,sobolT,sig2] = sobol_elm(W,beta,bias); % 最后这个函数计算灵敏度指数

四、绘图

五、代码获取

私信回复“84期”即可获取下载链接。