朴素贝叶斯算法

概率

一件事情发生的可能性，取值在【0,1】之间。比如：抛硬币正面向上的概率、6面骰子抛出5这一

面的概率

例子: 判断女神对你的喜欢情况

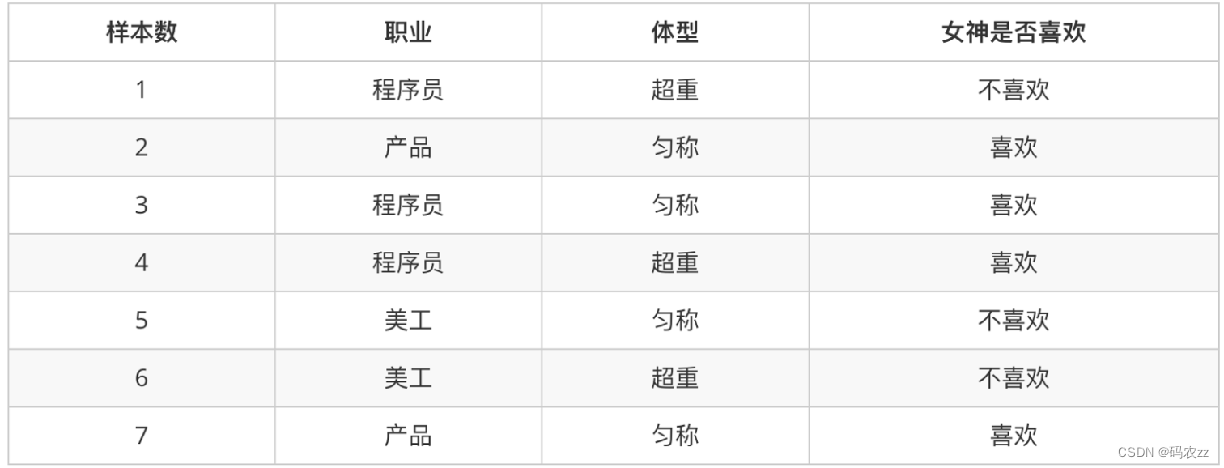
?条件概率：

表示事件A在另外一个事件B已经发生条件下的发生概率，P(A|B)

比如：在女神喜欢的条件下，职业是程序员的概率？

????????女神喜欢条件下，有 2、3、4、7 共 4 个样本

????????4 个样本中，?有程序员 3、4 共 2 个样本

????????则 P(程序员|喜欢) = 2/4 = 0.5

联合概率：

表示多个条件同时成立的概率，P(AB) = P(A) * P(B|A) = P(B)* P(A|B)

比如：职业是程序员并且体型匀称的概率？

????????数据集中，共有 7 个样本

????????职业是程序员有 1、3、4 共 3 个样本，则其概率为：3/7

????????在职业是程序员，体型是匀称有 3 共 1 个样本，

????????则其概率为：1/3 则即是程序员又体型匀称的概率为：3/7 * 1/3 = 1/7

联合概率 + 条件概率

比如：在女神喜欢的条件下，职业是程序员、并且超重的概率？ P(程序员, 超重|喜欢)

????????在女神喜欢的条件下，有 2、3、4、7 共 4 个样本

????????在这 4 个样本中，职业是程序员有 3、4 共 2 个样本，则其概率为：2/4=0.5

????????在这 2 个样本中，体型超重的有 4 共 1 个样本，

????????则其概率为：1/2 = 0.5 则 P(程序员, 超重|喜欢) = 0.5 * 0.5 = 0.25

相互独立：

如果P(A, B) = P(A)P(B)，则称事件A与事件B相互独立

比如：女神喜欢程序员的概率，女神喜欢产品经理的概率，两个事件没有关系

简而言之 ? ? ? ?

条件概率：在去掉部分样本的情况下，计算某些样本的出现的概率，表示为：P(B|A) ? ? ? ?

联合概率：多个事件同时发生的概率是多少，表示为：P(AB) = P(B)*P(A|B)

贝叶斯公式

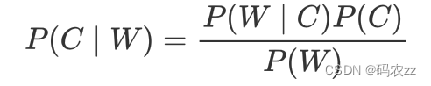
P(C) 表示 C 出现的概率，一般是目标值

P(W|C) 表示 C 条件 W 出现的概率

P(W) 表示 W 出现的概率

朴素贝叶斯

朴素贝叶斯在贝叶斯基础上增加：特征条件独立假设，即：特征之间是互为独立的

为了避免概率值为 0，我们在分子和分母分别加上一个数值，这就是拉普拉斯平滑系数的作用? ? ? ??

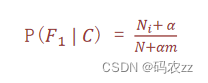
?α 是拉普拉斯平滑系数，一般指定为 1

Ni 是 F1 中符合条件 C 的样本数量

N 是在条件 C 下所有样本的总数

m 表示所有独立样本的总数

朴素贝叶斯API

sklearn.naive_bayes.MultinomialNB(alpha = 1.0）         
# 朴素贝叶斯分类
# alpha：拉普拉斯平滑系数

案例

需求:

已知商品评论数据，根据数据进行情感分类（好评、差评）

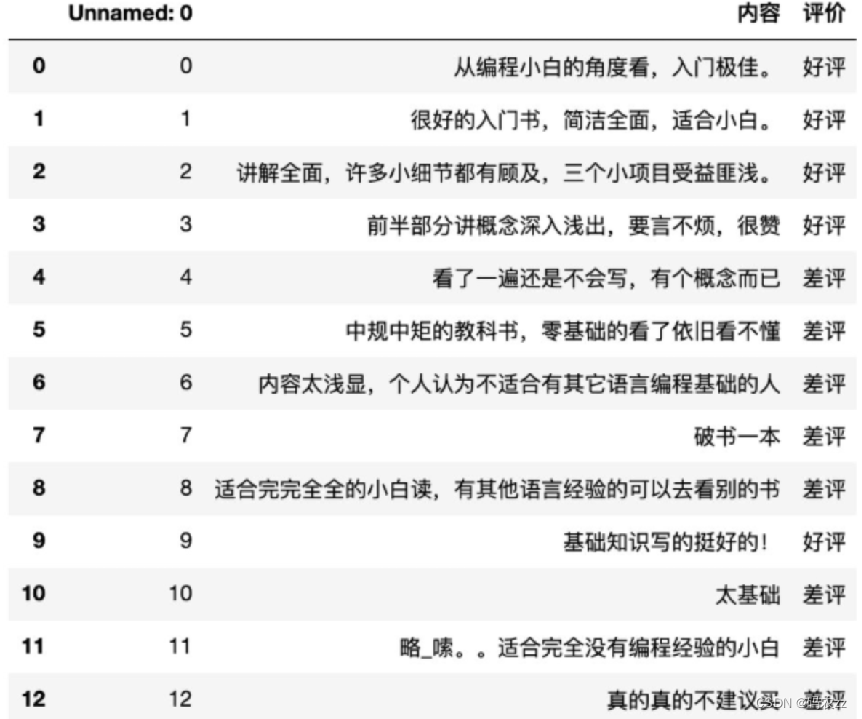
?分析流程:

1 获取数据

2 数据基本处理 ? ?

????????2-1 处理数据y? ? ?

????????2-2 加载停用词? ? ?

????????2-3 处理数据x 把文档分词? ? ?

????????2-4 统计词频矩阵 作为句子特征?

3 准备训练集测试集

4 模型训练? ? ?

????????4-1 实例化贝叶斯 添加拉普拉斯平滑参数? ? ?

????????4-2 模型预测

5 模型评估

代码示例

import numpy as np
import pandas as pd
import jieba  # 中文分词
from sklearn.feature_extraction.text import CountVectorizer
# 词频统计的库(文本转为向量)   feature_extraction特征抽取
from sklearn.naive_bayes import MultinomialNB  # 朴素贝叶斯
#%%
# 一: 读数据
data = pd.read_csv('书籍评价.csv',encoding='gbk')
#%%
# 增加一列
# np.where(条件, 满足条件时的取值, 不满足条件时的取值)
data['lable'] = np.where(data['评价']=='好评',1,0)
y = data['lable']
data
#%%
# 二: 加载停用此表
stopwords = []
with open('stopwords.txt','r',encoding='utf-8') as f:
    lines = f.readlines()
    stopwords = [line.strip() for line in lines]  # 去掉\n 空格 制表符
    stopwords = list(set(stopwords))  # 放到集合里,做去重,去重后,在变成列表
    
    

#%%
# 三:  处理特征
jieba.lcut(data['内容'][1])

# 三: 拼接成一个列表

# # jieba 中文分词工具
comment_list = [','.join(jieba.lcut(line)) for line in data['内容']]
comment_list 
#%%
# 使用CountVectorizer 对评论文本列表进行处理, 得到每个单词作为一个特征的 特征数据
# 加载之前处理好的停用词表  通过 stop_words参数传进来
count_vec = CountVectorizer(stop_words=stopwords) # 过滤器
x = count_vec.fit_transform(comment_list)
count_vec
#%%
# 数组化  显示
x.toarray()
#%%
# 新版本的 sklearn count_vec.get_feature_names_out()
count_vec.get_feature_names() # 打印所有出现的单词
#%%
## 使用朴素贝叶斯进行文本分类
x_train = x[:10,:] # 训练集
y_train = y[0:10]

x_test = x[10:,:] # 训练集
y_test = y[10:]
#%%
# 创建朴素贝叶斯对象  默认拉普拉斯平滑系数是1
estimator = MultinomialNB()
estimator.fit(x_train,y_train)
y_pred = estimator.predict(x_test)
#%%
y_test
#%%
y_pred