数据结构：堆的三部曲 （一）堆的实现

1.堆的结构

1.1堆的定义理解

堆的逻辑结构为一颗完全二叉树，堆对于数据存储有一定的要求：这这棵树的任意一颗子树的根节点的值小于等于（或大于等于）其孩子节点的值。我们将根节点最大的堆叫做小堆，把根节点最大的堆叫做大堆。
堆的存储结构结构为数组，我们将堆的元素存储在一个数组之中。由于堆是完全二叉树，所以其节点下标之间满足以下关系：
parent = (child-1) / 2
leftChild = parent2 + 1
rightChild = parent2 + 2 = leftChild + 1

堆的结构如图：

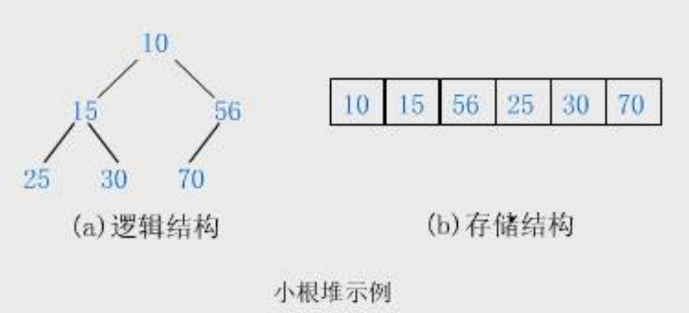
注意：堆规定的是父亲和孩子之间值的关系，并没有规定左右孩子值之间的关系。比如下图，我们对于15这个父节点的左右孩子大小没有要求，两种情况都可以，因此我们只需要维护父亲和孩子的关系即可。

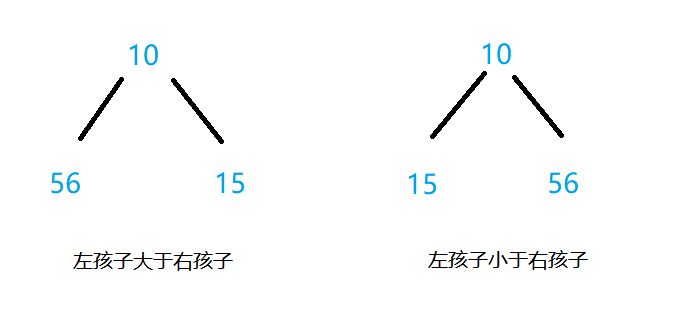
2.堆的实现（以小根堆为例）

2.1 堆结构体的定义

由于堆是使用数组来存储的，因此堆的结构定义和顺序表相同，首先需要定义一个数据类型的指针，然后还需要定义int类型的size和capacity，用来记录当前有多少个节点以及当前最多能存储多少节点，当空间不足时我们就可以扩容操作。

typedef int HpDataType;
typedef struct Heap
{
	HpDataType* a;
	int size;
	int capacity;
}HP;

2.2 堆的插入

堆的插入的前提是插入前的二叉树是堆，因此插入数据后只需要保持其父亲节点和孩子节点的关系。由于使用数组存储，因此在size位置插入后，就需要开始调整使插入后仍为堆。

交换函数

void Swap(HpDataType* x, HpDataType* y)
{
	HpDataType tmp = *x;
	*x = *y;
	*y = tmp;
}

向上调整算法

由于是从插入的那个孩子处开始调整，所以需要传入当时的下标。
child即为最后一个节点的下标。由于需要维护每一个父亲和孩子的关系，因此需要用到循环。如果新插入的节点的值比父节点的值小，那么交换它们的值，如果比其的父节点的值大，那么插入节点后的堆仍为小堆，不需要调整，退出循环。考虑最坏情况，如果插入的节点比第一个节点的值都小，那么就需要一直交换，当最后一个节点也调整后，不满足条件从而退出循环，那么这个最坏的结果结束后的child即为最终的循环结束条件，此时child为0，因此循环进行条件为child>0，结束条件为child<=0。

void AdjustUp(HpDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

插入函数的代码

void HPPush(HP* hp, HpDataType x)
{
	assert(hp);
	int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
	//空间如果不足则扩容
	if (hp->capacity == hp->size)
	{
		HpDataType* tmp = (HpDataType*)realloc(hp->a, newcapacity*sizeof(HpDataType));
		if (tmp == NULL)
		{
			perror("realloc failed");
			exit(-1);
		}
		hp->a = tmp;
		hp->capacity = newcapacity;
	}
	hp->a[hp->size] = x;
	hp->size++;
	AdjustUp(hp->a, hp->size - 1);
}

2.3 堆的删除

堆的删除为删除堆顶元素。
如果我们直接使用数据移动覆盖的删除方法，那么基本所有的父子关系将会被打乱，这样堆就会被完全破坏，而顺序表删除最后一个元素很容易，因此我们可以将第一个节点和最后一个节点交换，再删除最后一个节点，这样不仅更加简便，而且根节点的左右子树仍为堆，我们只需要将根节点向下调整即可调整为堆。

向下调整算法：

那么如何实现向下调整算法呢？
我们需要让每一颗子树的根节点都为该树的最小值，由于堆没有规定左右孩子之间的关系，因此如果需要向下调整交换时，需要判断该节点的左右孩子的最小值。如果不需要交换，即该节点比孩子节点小，那么就证明此时为堆，结束循环。考虑最坏情况，直到交换到叶子节点才能结束，那么如何判断叶子节点呢？叶子节点是没有孩子的节点，也就是其孩子的下标超出了size的大小，因此通过child和size的大小可以判断是否为叶子节点。

void AdjustDown(HpDataType* a, int size, int parent)
{
	int child = parent * 2 + 1;

	while (child < size)
	{
		//假设左孩子小，如果假设错误则交换
		if (child + 1 < size && a[child] > a[child + 1])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

删除函数的代码：

void HPPop(HP* hp)
{
	assert(hp);
	assert(hp->size > 0);

	Swap(&hp->a[0], hp->a[hp->size - 1]);
	hp->size--;
	AdjustDown(hp->a, hp->size, 0);
}

2.4其他操作

2.4.1取堆顶元素

int HPTop(HP* hp)
{
	assert(hp);

	return hp->a[0];
}

2.4.2堆的节点个数

int HPSize(HP* hp)
{
	assert(hp);

	return hp->size;
}

2.4.3堆是否为空判断

bool IsEmpty(HP* hp)
{
	assert(hp);

	return hp->size == 0;
}

3.测试以及完整源代码实现

3.1测试代码

int main()
{
	int a[] = { 3,5,2,7,9,4,1 };
	HP hp;
	HPinit(&hp);
	//建堆
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		HPPush(&hp, a[i]);
	}
	//打印堆
	for (int i = 0; i < hp.size; i++)
	{
		printf("%d ", hp.a[i]);
	}
	printf("\n");
	//类似堆排序
	while (!IsEmpty(&hp))
	{
		printf("%d ", HPTop(&hp));
		HPPop(&hp);
	}
	printf("\n");
	//类似top  k
	//int k = 3;
	//while (k--)
	//{
	//	printf("%d ", HPTop(&hp));
	//	HPPop(&hp);
	//}

	HPDestroy(&hp);
	return 0;
}

运行结果如下：

3.2完整代码实现

heap.c

#pragma once

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>

typedef int HpDataType;
typedef struct Heap
{
	HpDataType* a;
	int size;
	int capacity;
}HP;

void HPinit(HP* hp);
void HPDestroy(HP* hp);
void HPPush(HP* hp, HpDataType x);
void HPPop(HP* hp);
int HPTop(HP* hp);
bool IsEmpty(HP* hp);
int HPSize(HP* hp);

heap.c

//小堆的实现
void HPinit(HP* hp)
{
	assert(hp);
	hp->a = NULL;
	hp->size = hp->capacity = 0;
}

void HPDestroy(HP* hp)
{
	assert(hp);
	free(hp->a);
	hp->a = NULL;
	hp->capacity = hp->size = 0;
}

void Swap(HpDataType* x, HpDataType* y)
{
	HpDataType tmp = *x;
	*x = *y;
	*y = tmp;
}

void AdjustUp(HpDataType* a, int child)
{
	int parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (parent - 1) / 2;
		}
		else
		{
			break;
		}
	}
}

void HPPush(HP* hp, HpDataType x)
{
	assert(hp);
	if (hp->capacity == hp->size)
	{
		int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
		HpDataType* tmp = (HpDataType*)realloc(hp->a, newcapacity * sizeof(HpDataType));
		if (tmp == NULL)
		{
			perror("realloc failed");
			exit(-1);
		}
		hp->a = tmp;
		hp->capacity = newcapacity;
	}
	hp->a[hp->size] = x;
	hp->size++;
	AdjustUp(hp->a, hp->size - 1);
}

void AdjustDown(HpDataType* a, int size, int parent)
{
	int child = parent * 2 + 1;

	while (child < size)
	{
		//假设左孩子小，如果假设错误则交换
		if (child + 1 < size && a[child] > a[child + 1])
		{
			child++;
		}
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void HPPop(HP* hp)
{
	assert(hp);
	assert(hp->size > 0);

	Swap(&hp->a[0], &hp->a[hp->size - 1]);
	hp->size--;
	AdjustDown(hp->a, hp->size, 0);
}

int HPTop(HP* hp)
{
	assert(hp);

	return hp->a[0];
}

bool IsEmpty(HP* hp)
{
	assert(hp);

	return hp->size == 0;
}

int HPSize(HP* hp)
{
	assert(hp);

	return hp->size;
}

main.c

#include "heap.h"

int main()
{
	int a[] = { 3,5,2,7,9,4,1 };
	HP hp;
	HPinit(&hp);
	for (int i = 0; i < sizeof(a) / sizeof(int); i++)
	{
		HPPush(&hp, a[i]);
	}
	printf("建堆如下:");
	for (int i = 0; i < hp.size; i++)
	{
		printf("%d ", hp.a[i]);
	}
	printf("\n");
	printf("依次取堆顶元素:");
	while (!IsEmpty(&hp))
	{
		printf("%d ", HPTop(&hp));
		HPPop(&hp);
	}
	printf("\n");
	//int k = 3;
	//while (k--)
	//{
	//	printf("%d ", HPTop(&hp));
	//	HPPop(&hp);
	//}
	HPDestroy(&hp);
	return 0;
}

以上就是本次说有内容，谢谢观看。