数据结构(C语言版)第五章树和二叉树
目录

5.1 树和二叉树的定义
5.1.1 树的定义
树是n(n>=0)个结点的有限集,当n等于0时为空树,当n不等于0时为非空树。
在树形结构中,元素间的关系为------1:n。
对于非空树T:
(1)有且仅有一个称之为根的节点
(2)除根节点以外的其余节点可分为m(m>0)个互不相交的有限集T1,T2,T3...Tm,其中每个集合本身又是一棵树,并且称为根的子树。
数的结构定义是一个递归的定义,它是树的固有特性,我们在构造树的过程,以及在对树中结点进行操作时,都要用到递归。
树的几种表示方法:

?5.1.2 树的基本术语
结点:树中的一个独立单元。
结点的度:结点拥有的子树数称为结点的度。
树的度:树内各结点度的最大值称为树的度。
叶子(结点):度为0的结点称为叶子(结点)或终端结点。
反之,度不为0的结点称为非终端结点或分支结点。(除了根结点以外,非终端节点也称为内部结点。)
双亲和孩子:结点的子树的根称为该结点的孩子,相应地,该结点称为孩子的双亲。
兄弟:同一个双亲的孩子之间互称为兄弟。
祖先:从根到该结点所经分支上的所有节点。
子孙:以某结点为根的子树中的任一结点都称为该结点的子孙。
层次:结点的层次从根开始定义,根为第一层,根的孩子为第二层,依次类推。
堂兄弟:双亲在同一层的结点互为堂兄弟(树中处于同一层次的结点)
树的深度:树中结点的最大层次称为树的深度或高度。
森林:m(m>=0)棵互不相交的树的集合。
5.1.3 二叉树的定义
?二叉树是n(n>=0)个结点所构成的集合,当n等于0时为空树,当n不等于0时为非空树。
对于非空树T:
(1)有且仅有一个称之为根的结点。
(2)除根结点以外的其余结点分为两个互不相交的子集T1和T2,分别称为T的左子树和右子树,且T1和T2本身又都是二叉树。
二叉树与树一样具有递归性质。
二叉树与树的区别:
(1)二叉树的每个结点至多只有两棵子树(二叉树中不存在度大于2的结点)
(2)二叉树的子树有左右之分,其次序不能任意颠倒。
5.2?二叉树的定义类型
?1.InitBiTree(&T)? 构造一棵空的二叉树T
2.CreateBiTree(&T)? 构造二叉树T
3.Value(T,e)? 返回二叉树T中e的值
4.PreOrderTraverse(T)? 先序遍历二叉树T
5.InOrderTraverse(T) 中序遍历二叉树T
6.PostOrTraverse(T)? 后序遍历二叉树T
7.LevelorderTraverse(T)? 层次遍历二叉树T
8.BiTreeEmpty(T)? 判断二叉树T是否存在
9.BiTreeDepth(T)? 返回二叉树T的深度
10.DestroyBiTree(T)? 销毁二叉树T
11.Copy(T,NewT)? 复制一棵和二叉树T完全相同的二叉树NewT
12.NodeCount(T)? 统计二叉树T中结点的个数
13.NodeCount1(T)? 统计二叉树中叶子结点的个数
5.3?二叉树的性质和存储结构?
?5.3.1 二叉树的性质
满二叉树:深度为k且含有
-1个结点的二叉树。
满二叉树的特点:每一层上的结点数都是最大的结点数,即
(i>=1)个结点。
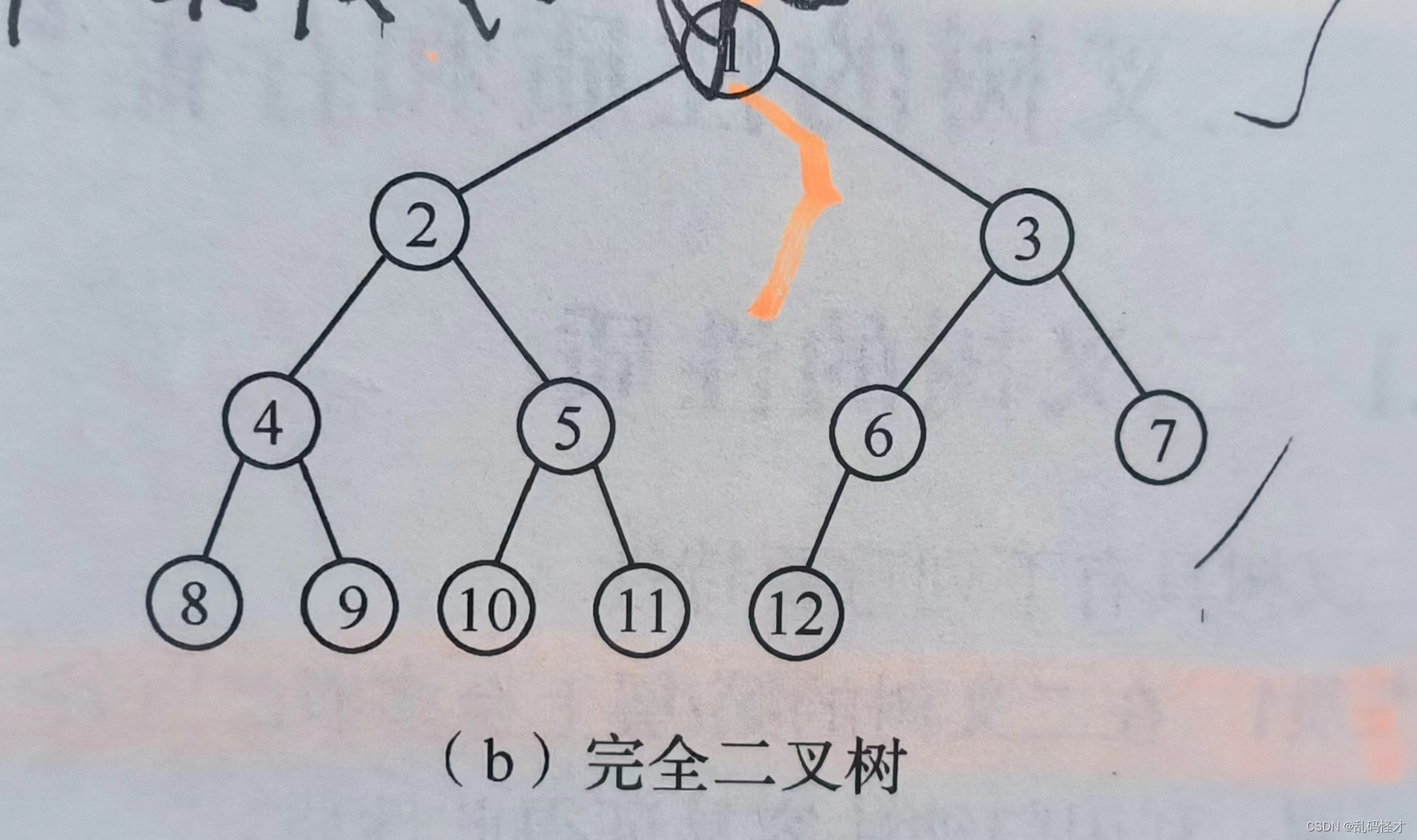
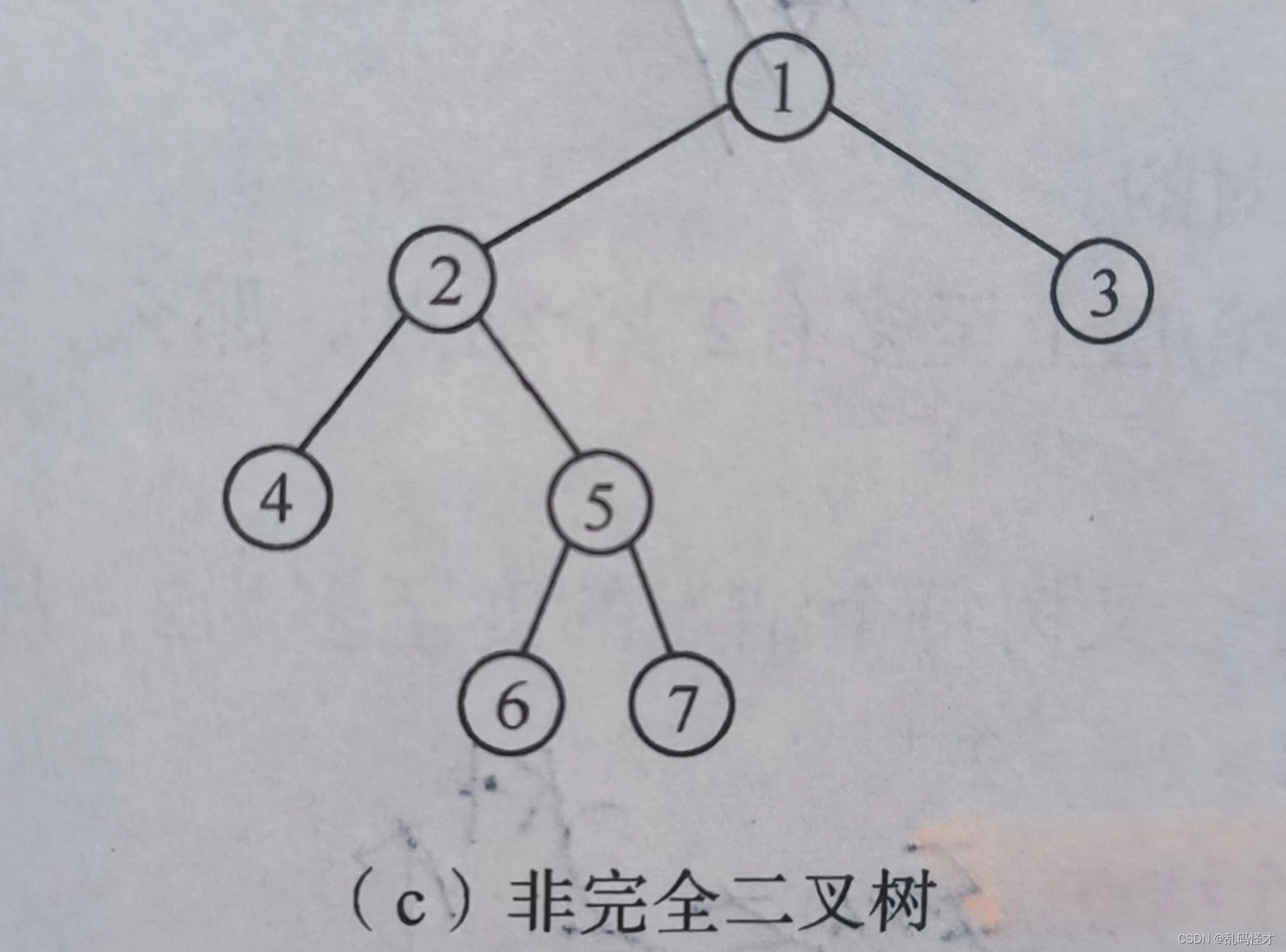
完全二叉树:深度为k,有n个结点的二叉树,并且每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应。
完全二叉树的特点:
①叶子节点只可能在层次最大的两层出现。
②度为1的结点数要么为1,要么为0。
?性质一:在二叉树的第i层上至多有
(i>=1)个结点。(至少有1个结点)
性质二:深度为k的二叉树至多有
(k>=1)个结点。(至少有
个结点)
性质三:对于任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。
性质四:具有n个结点的完全二叉树的深度为
(向下取整)+1。
5.3.2? 二叉树的存储结构
?1.顺序存储结构
顺序存储结构使用一组地址连续的存储单元来存储数据元素。
对于完全二叉树,按照层序存储即可。
对于一般二叉树,则应将每个结点与完全二叉树上的结点相照应,存储在一维数组的相应分量中。
例如:
顺序存储只适用于完全二叉树,而对于一般的二叉树,会浪费存储空间,因此,对于一般的二叉树更适合采用链式存储结构。
2.链式存储结构?
由二叉树的定义可知,二叉树的结点由一个数据元素和分别指向其左,右子树的两个分支构成,则表示二叉树的链表中至少包含三个域:数据域和左,右指针域。
有时为了便于找到结点的双亲,还可以在结点结构中增加一个指向其双亲的指针域,从而得到另一种链式存储结构-------线索链表。
二叉树的链式存储表示:
typedef char TElemType;
typedef struct BiTNode{
TElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;5.4 二叉树的基本操作(算法表述)
1.先序遍历创建二叉树
void CreateBiTree(BiTree &T){//先序遍历建立二叉树
TElemType ch;
cin>>ch;
if(ch=='#') T=NULL;
else
{
T=new BiTNode;
T->data=ch;
CreateBiTree(T->lchild);
CreateBiTree(T->rchild);
}
}2.先序遍历二叉树(递归)
void PreOrderTraverse(BiTree T){//先序递归遍历输出二叉树
if(T)
{
cout<<T->data;
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
}3.中序遍历二叉树(递归)
void InOrderTraverse(BiTree T){//中序递归遍历输出二叉树
if(T)
{
InOrderTraverse(T->lchild);
cout<<T->data;
InOrderTraverse(T->rchild);
}
}4.后序遍历二叉树(递归)
void PostOrderTraverse(BiTree T){//后序递归遍历输出二叉树
if(T)
{
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
cout<<T->data;
}
}5.复制二叉树
void Copy(BiTree T,BiTree &NewT){//复制二叉树
if(T==NULL)
{
NewT=NULL;
return;
}
else
{
NewT=new BiTNode;
NewT->data=T->data;
Copy(T->lchild,NewT->lchild);
Copy(T->rchild,NewT->rchild);
}
}6.统计二叉树中结点的个数
int NodeCount(BiTree T){//统计二叉树中结点的个数
if(T==NULL) return 0;
else return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
}7.统计二叉树中叶子结点的个数
int NodeCount1(BiTree T){//统计二叉树中叶子节点的个数
if(T==NULL) return 0;
else if(T->lchild==NULL&&T->rchild==NULL) return 1;
else return NodeCount1(T->lchild)+NodeCount1(T->rchild);
}?8.计算二叉树的深度
int Depth(BiTree T)//计算二叉树的深度
{
if(T==NULL) return 0;
else
{
m=Depth(T->lchild);
n=Depth(T->rchild);
if(m>n) return (m+1);
else return (n+1);
}
}5.5 线索二叉树
我们为什么要定义线索二叉树?
答:在二叉树的遍历中,我们可以利用递归函数依次访问结点的左右孩子结点,从而得到二叉树的先序遍历,中序遍历和后序遍历,但是我们无法直接得到结点在任一序列中的前驱和后继信息,这种信息只有在遍历的动态过程中才能得到,为此引入线索二叉树来保存这些在动态过程中得到的有关前驱和后继的信息。
二叉树的二叉线索存储表示:
typedef struct BiThrNode
{
TElemType data;
struct BiThrNode *lchild,*rchild;//左右孩子指针
int LTag,RTag;//左右孩子标志
}BiThrNode,*BiThrTree;线索链表:以上面这种结构构成的二叉链表作为二叉树的存储结构,叫作线索链表。
线索:指向结点前驱和后继的指针,叫作线索。(加上线索的二叉树称之为线索二叉树)
线索化:对二叉树以某种次序遍历使其变成线索二叉树的过程,叫作线索化。
线索二叉树的相关考研真题:
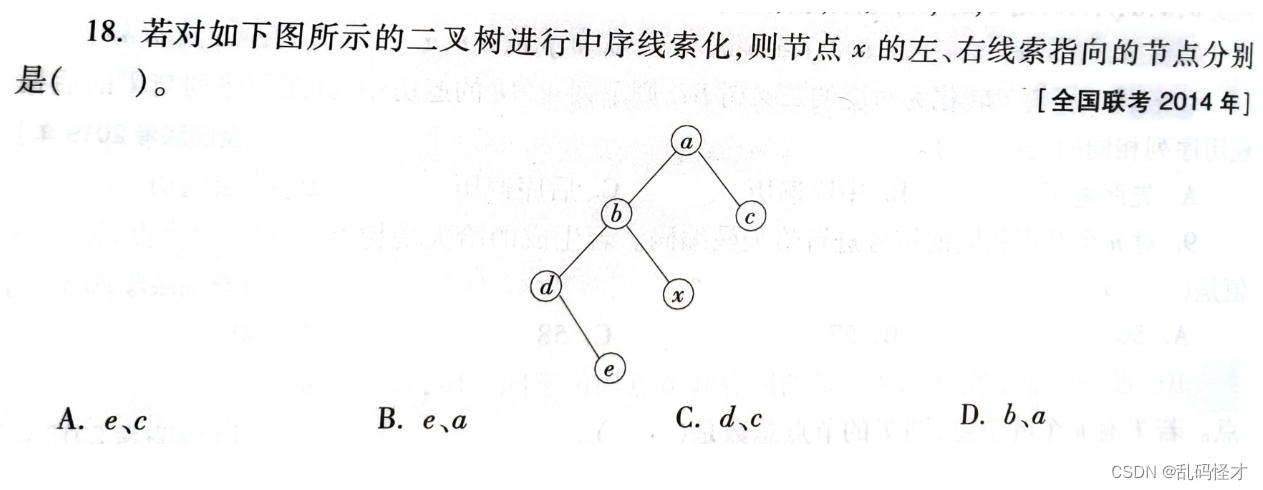
解析:
18.【答案】D。
【考点】树与二叉树——二叉树
【解析】指向节点前驱和后继的指针称为线索,带有线索的二叉树称为线索二叉树。本题中,二叉树进行中序遍历的序列为d,e,b,x,a,c,中序遍历序列中在左、右边的元素分别是节点x的左、右线索,则节点x的左线索指向的是节点b,右线索指向的是节点a。

?解析:
27.【答案】D。
【考点】树与二叉树——二叉树
【解析】该线索二叉树的后序遍历序列是d,b,c,a。节点d是叶节点,其左、右链域都为空,在转换成线索二叉树后,其左链域指向前驱节点,但是节点d没有前驱节点,因此左链域为Null,排除B、C两项,右链域指向后继节点b,排除选项A。选项D符合后序线索树定义。
?34.在含有N个节点的线索二叉树中线索的数目为(? )。【暨南大学2022】
A.2N? ? ? ? ? ?B.N? ? ? ? ? C.N-1? ? ? ? ? D.N+1
解析:
34.【答案】D。
【考点】树与二叉树——二叉树
【解析】采用二叉链表存储含有N个节点的二叉树时,有N+1个指针域必定为空,线索二叉树中,用这N+1个空指针域存放指向节点的直接前驱和直接后继的指针,这种指针称为线索,因此线索有N+1个。
在线索二叉树的考研题目中,大题部分还会考画出某棵树的先序或后序或中序线索二叉树,做法很简单,首先写出这棵树的某序序列,然后根据序列连线即可。
5.6 树和森林
5.6.1 树的存储结构
1.双亲表示法
2.孩子表示法
3.孩子兄弟表示法(较为普遍的一种树的存储表示方法)
孩子兄弟表示法又称为二叉树表示法,或二叉链表表示法,即以二叉链表作为树的存储结构,链表中结点的两个链域分别指向该结点的第一个孩子和下一个兄弟结点。
5.6.2森林与二叉树的转换
从树的二叉链表表示的定义可知,任何一棵和树对应的二叉树,其根结点的右子树必为空。
??
总结的两个规律:
1.森林的结点数=森林中树的边数+森林中树的棵数。
2.树的结点数=树的边数+1
?1.森林转换成二叉树
森林中第一棵树的根结点作为二叉树的根结点,二叉树根结点的左孩子为第一棵树的根结点的左孩子,二叉树根结点的右孩子为第一棵树的根结点的左孩子的相邻兄弟结点,依次类推就可得到对应的二叉树。
?2.二叉树转换成森林
由孩子兄弟法的性质可知,在将树转化为二叉树时,这棵二叉树的右子树必为空,因此我们可以从二叉树的右子树入手,根结点的右孩子结点一定是第二棵树的根结点,而根结点的右孩子的右孩子也一定是第三棵树的根结点,依次类推,我们可以得到森林中所有树的根结点,然后这些根结点的左子树部分就是相对应的树中的结点,最后我们利用孩子兄弟法的存储规律就可以顺利的将二叉树转换成森林了。
5.6.3 树和森林的遍历
1.树的遍历
树的遍历与二叉树遍历一样,分三种------先序遍历,中序遍历和后序遍历。
2.森林的遍历
森林的遍历其实就是森林中每棵树按照顺序依次进行指定的序列遍历。
当以二叉链表作为树的存储结构时,树的先根遍历和后根遍历可借助二叉树的先序遍历和中序遍历实现。
5.7 哈夫曼树及其应用
?5.7.1 哈夫曼树的基本概念
哈夫曼树又称最优树,是一类带权路径长度最短的树,在实际中有广泛的用途。
路径:从树的一个结点到另一个结点之间的分支构成这两个结点之间的路径。
路径长度:路径上的分支数目称作路径长度。
树的路径长度:从数根到每一结点的路径长度。
权:在数据结构中,实体有结点(元素)和边(关系)两大类,所以对应有结点权和边权。
结点的带权路径长度:从该结点到树根之间的路径长度与结点上权值的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和,通常记作WPL。
哈夫曼树:m个有权值的结点构成的带权路径长度最小的二叉树。(哈夫曼树也叫作最优二叉树)
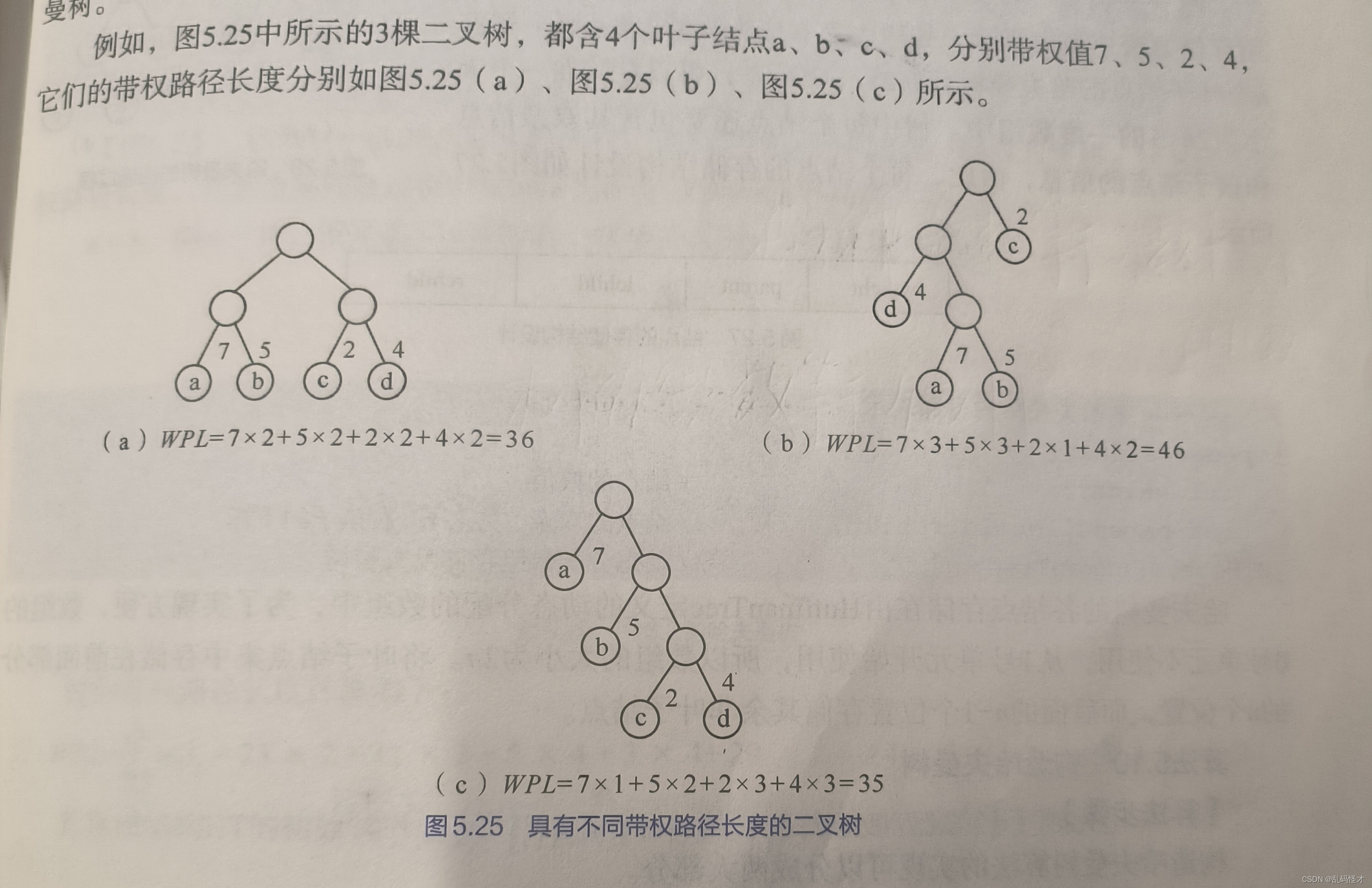
上图中(C)二叉树的带权路径长度(WPL)最小,因此可以验证它恰为哈夫曼树。
在上面的例子中,我们不难发现,在哈夫曼树中,权值越大的结点离根结点越近。根据这个特点,哈夫曼最早给出了一个构造哈夫曼的方法,称为哈夫曼算法。
下面,我们将介绍如何去人为去构造一棵哈夫曼树。系好安全带,我们准备发车了!
?5.7.2 哈夫曼树的构造算法
1.哈夫曼树的构造过程
我们举例说明:
现有四个结点a,b,c,d,其权值分别为7,5,2,4,构造出一棵哈夫曼树。
第一步:我们找出这些权值中最小的两个结点,它们分别是2和4。
第二步:将2和4作为左右孩子结点,将它们的权值相加得到双亲结点,其权值为6。
第三步:将权值为2和4的结点从集合中消去,将6写在5的后面。
第四步:重复第一,二,三步过程,直至结点全部用完。
我们来看相关的考研真题:
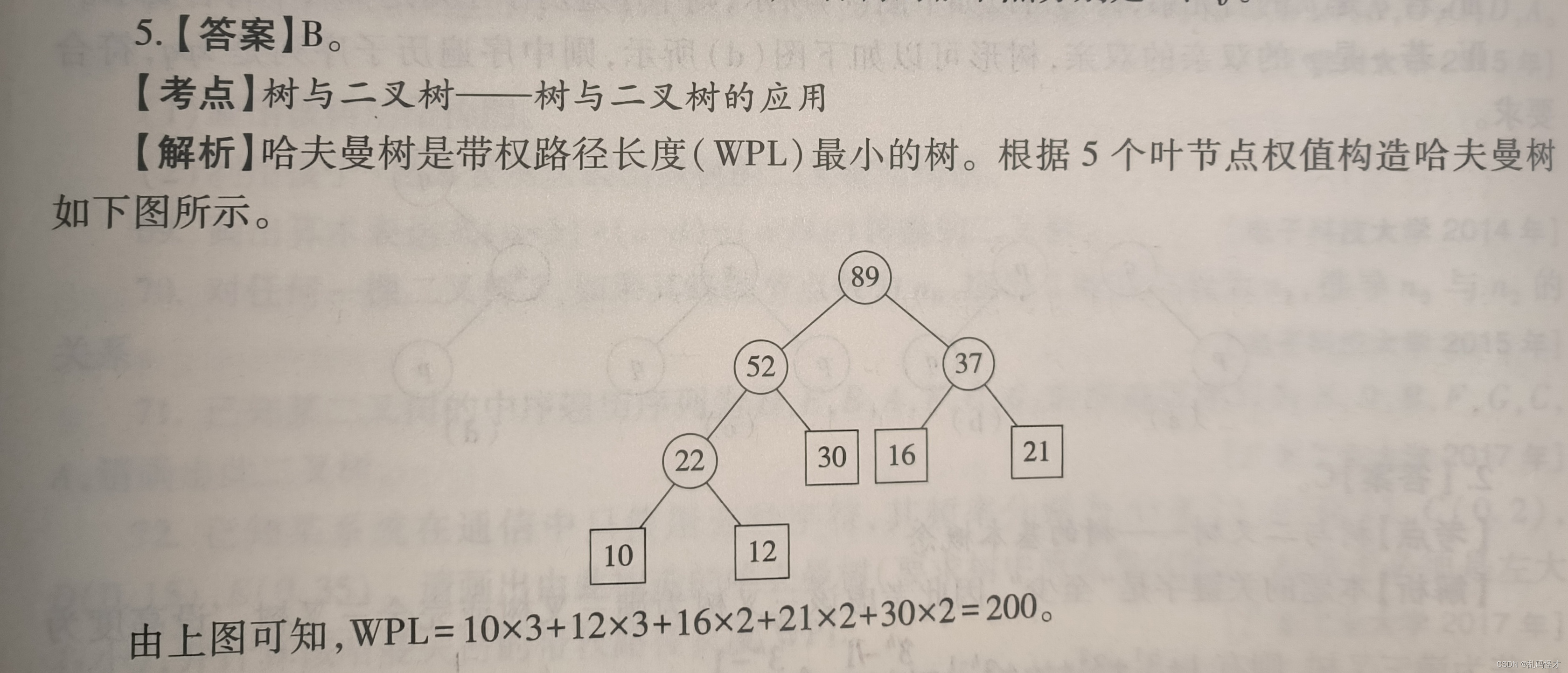
?5.若某二叉树有5个叶节点,其权值分别为10,12,16,21,30,则其最小的带权路径长度WPL是()【全国联考2021年】
A.89? ? ? ? ? ? B. 200? ? ? ? ? C.208? ? ? ? ? D.289
解析:
2.哈夫曼树算法的实现
?哈夫曼树是一种二叉树,可以采用二叉树的通用存储方法,而由于哈夫曼树中没有度为1的结点,则一棵有n个叶子结点的哈夫曼树共有2n-1个结点,可以存储在一个大小为2n-1的一维数组中。
树中的每个结点还要包含其双亲信息和孩子结点的信息,由此,每个结点的存储结构可以设计成如下所示:
哈夫曼树的存储表示:
typedef struct
{
int weight;//结点的权值
int parent,lchild,rchild;//结点的双亲,左孩子,右孩子的下标
}HTNode,*HuffmanTree;//动态分配数组存储哈夫曼树?构造哈夫曼树:
void Select(HuffmanTree HT,int n,int &s1,int &s2)//查找权值最小的两个结点的下标
{
int min;
for(int i=1;i<=n;i++)//找到一个未使用的节点
{
if(HT[i].parent==0)
{
min=i;
break;
}
}
for(int i=min+1;i<=n;i++)//找出节点最小值的下标
{
if(HT[i].parent==0&&HT[i].weight<HT[min].weight)
{
min=i;
}
}
s1=min;
for(int i=1;i<=n;i++)
{
if(HT[i].parent==0&&i!=s1)
{
min=i;
break;
}
}
for(int i=min+1;i<=n;i++)
{
if(HT[i].parent==0&&HT[i].weight<HT[min].weight&&i!=s1)
{
min=i;
}
}
s2=min;
}
void CreateHuffmanTree(HuffmanTree &HT,int n)
{
if(n<=1)
return;
int m=2*n-1;
HT=new HTNode[m+1];
cout<<"请输入相应的权值:";
for(int i=1;i<=n;i++)
{
cin>>HT[i].weight;
getchar();
HT[i].parent=0;
HT[i].lchild=0;
HT[i].rchild=0;
}
for(int i=n+1;i<=m;i++)
{
HT[i].weight=0;
HT[i].parent=0;
HT[i].lchild=0;
HT[i].rchild=0;
}
cout<<"哈夫曼树的初始状态为:\n";
cout<<"下标 weight parent lchild rchild\n";
for(int j=1;j<=m;j++)
{
printf("%-8d%-8d%-8d%-8d%-8d\n",j,HT[j].weight,HT[j].parent,HT[j].lchild,HT[j].rchild);
}
cout<<"\n";
for(int i=n+1;i<=m;i++)
{
int s1,s2;//s1为节点的最小值的下标,s2为节点的次小值的下标
Select(HT,i-1,s1,s2);
HT[i].weight=HT[s1].weight+HT[s2].weight;
HT[s1].parent=i;
HT[s2].parent=i;
HT[i].lchild=s1;
HT[i].rchild=s2;
}
cout<<"哈夫曼树的终结状态为:\n";
cout<<"下标 weight parent lchild rchild\n";
for(int i=1;i<=m;i++)
{
printf("%-8d%-8d%-8d%-8d%-8d\n",i,HT[i].weight,HT[i].parent,HT[i].lchild,HT[i].rchild);
}
}?以w=(5,29,7,8,14,23,3,11)为例,构造哈夫曼树。??
? ? ? ? ? ? ? ??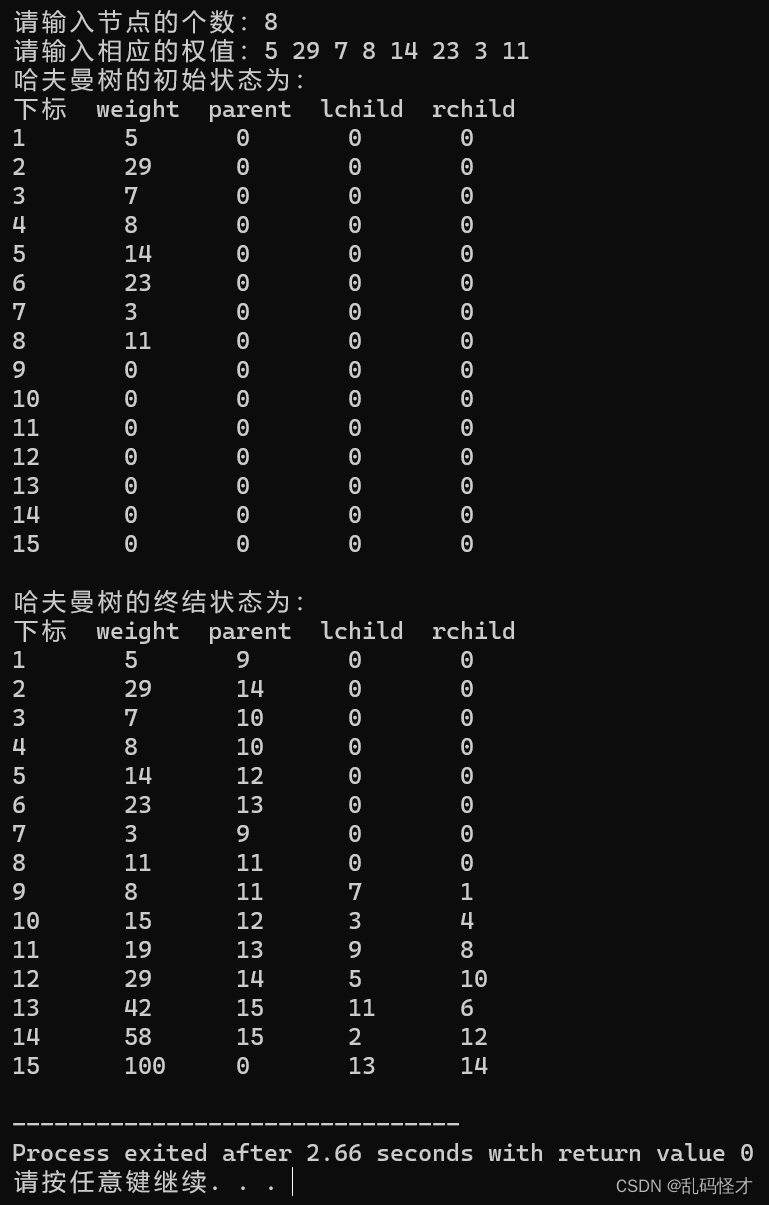 ?
?
5.7.3 哈夫曼编码
在一个给定的哈夫曼树中,约定左分支为0,右分支为1,则根结点到叶子结点路径上的0,1序列即对应字符的编码。
哈夫曼编码的两个性质:
性质一:哈夫曼编码是前缀编码(等长编码属于前缀编码)。
性质二:哈夫曼编码是最优前缀编码。
算法描述:
void CreateHuffmanCode(HuffmanTree HT,HuffmanCode &HC,int n)//哈夫曼编码
{
char *cd;
int start,f,c;
HC=new char*[n+1];
cd=new char[n];
cd[n-1]='\0';
for(int i=1;i<=n;i++)
{
start=n-1;
c=i;
f=HT[i].parent;
while(f!=0)
{
start--;
if(HT[f].lchild==c) cd[start]='0';
else cd[start]='1';
c=f;f=HT[f].parent;
}
HC[i]=new char [n-start];
strcpy(HC[i],&cd[start]);
}
delete cd;
}?哈夫曼树的相关考研真题:
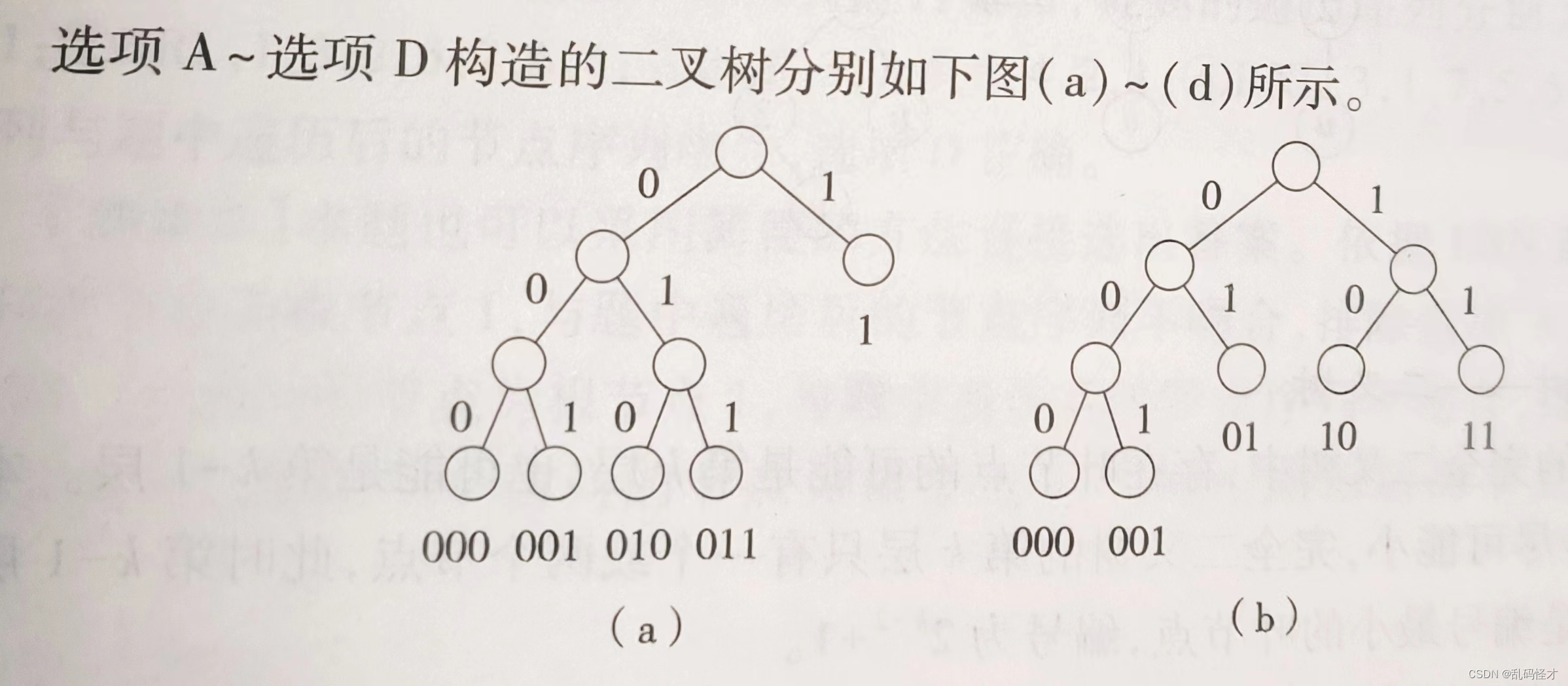
1.根据使用频率,为5个字符设计的哈夫曼编码不可能是(? )。[暨南大学2020年]
A. 000,001,010,011,1
B. 000,001,01,10,11
C. 00,100,101,110,111D. 0000,0001,001,01,1
解析:
我们知道哈夫曼树中是不存在度为1的结点,只有选项C包含度为1的结点,因此选C。
小结
?在计算机相关专业的考研中,数据结构中的二叉树是重中之重,大家要掌握到位。
在计算机考研中,全国统考科目为计算机专业学科基础,简称408,一共包含四门课程------数据结构,计算机组成原理,计算机网络和操作系统,其中数据结构和计算机组成原理较难,当然也有很多院校是自命题,除了部分院校的自命题难度较大外,其他院校自命题难度是要低于408的,大家考研要尽早准备,一起加油,我特别喜欢董卿老师说过的一段话,分享给大家:“每一个人都必定出发于他的少年时,只是很多年之后,蓦然回首,你是否还会记得那年少时的梦呢?年少的梦啊,有些很幸运地实现了,有些被遗忘在了风中,而什么时候有过什么样的一个梦,其实并不是很重要,重要的是,我们曾经为了这个梦,如此热烈地爱过,执着地追求过,勇敢地拼搏过,这是梦的意义,也是永远值得被记住的时光。”------2023年12月31日
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 达梦php_pdo不同机器安装
- 2024年【高处安装、维护、拆除】考试题及高处安装、维护、拆除模拟试题
- 由在美流浪的复旦博士,想到的debug哲学
- 密钥管理中心的主要功能是什么
- 小果量化网页---多标的投资组合分析,支持可转债,股票,ETF同时分析
- 题记(27)--寻找大富翁
- 【已解决】Atlas 导入 Hive 元数据,执行 import-hive.sh 报错
- 【Qt之Quick模块】6. QML语法详解_2类型系统
- 满足ITOM需求的网络监控工具
- UmiMax学习笔记