力扣刷题记录（28）LeetCode：797、200、463

797.?所有可能的路径

解题思路：回溯算法，当收集到的路径的最后一个值等于n-1时，收集答案。

参数：图、当前结点

?

class Solution {
public:
    vector<int> path;
    vector<vector<int>> ans;
    void dfs(vector<vector<int>>& graph,int index)
    {
        if(path.back()==graph.size()-1)
        {
            ans.push_back(path);
            return;
        }
        for(int i=0;i<graph[index].size();i++)
        {
            path.push_back(graph[index][i]);
            dfs(graph,graph[index][i]);
            //回溯
            path.pop_back();
        }
    }
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        //从0开始的，先将0传入路径中
        path.push_back(0);
        dfs(graph,0);
        return ans;
    }
};

200.?岛屿数量

解题思路：如果我们遍历到一块陆地，那我们就以这块陆地为中心向它的周围扩散，将所有与之相连的陆地全部都标记。这时我们所标记的所有相连的陆地就形成了一片岛屿，岛屿数量加一。那我们如果对所有陆地都进行这样的操作，就可以得到岛屿的数量。需要注意的是我们需要对已经标记过的陆地进行这样的操作，因为它已经是前面统计过的岛屿的一部分。

class Solution {
private:
    void dfs(vector<vector<char>>& grid,int x,int y)
    {
        //判断是否越界
        if(x>=grid[0].size() || y>=grid.size()) return;
        //判断岛屿是否遍历过 只遍历岛屿
        if(grid[y][x]=='2'||grid[y][x]=='0')  return;
        //将岛屿的状态改为遍历过
        grid[y][x]='2';
        dfs(grid,x-1,y);
        dfs(grid,x+1,y);
        dfs(grid,x,y-1);
        dfs(grid,x,y+1);

    }
public:
    int numIslands(vector<vector<char>>& grid) {
        int ans=0;
        for(int i=0;i<grid.size();i++)
        {
            for(int j=0;j<grid[0].size();j++)
            {
                if(grid[i][j]=='1')
                {
                    //将和该陆地连在一起的陆地的状态都改变为遍历过
                    dfs(grid,j,i);
                    ans++;
                }
            }
        }
        return ans;
    }
};

463.?岛屿的周长?

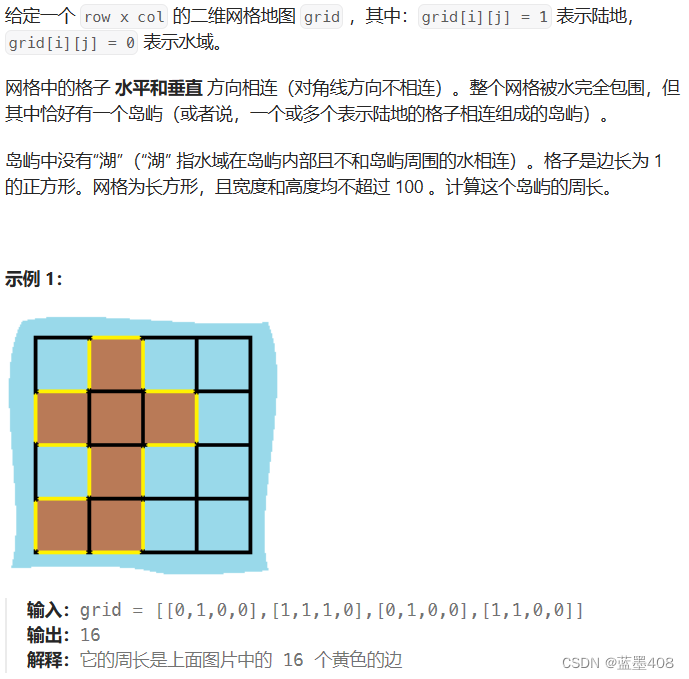
解题思路：深度优先遍历，可以向上下左右是个方向进行深度遍历。如果在某一方向上遍历到水或者超出了边界，那么这个方向上的周长就确定是1了。如果遍历到陆地则继续深入下去。需要注意的是对于遍历过的元素一定要做标记，否则将陷入死循环中。

class Solution {
public:
    int dfs(vector<vector<int>>& grid,int i,int j)
    {
        if( (i>=grid.size() || i<0) || (j>=grid[0].size()||j<0) )   return 1;
        if(grid[i][j]==0) return 1;
        //遍历过的将不再遍历 且持有的周长为0
        if(grid[i][j]==2)   return 0;
        //对遍历过的陆地进行标记
        grid[i][j]=2;
        return dfs(grid,i-1,j)+dfs(grid,i+1,j)+dfs(grid,i,j-1)+dfs(grid,i,j+1);
    }
    int islandPerimeter(vector<vector<int>>& grid) {
        for(int i=0;i<grid.size();i++)
        {
            for(int j=0;j<grid[0].size();j++)
            {
                if(grid[i][j]==1) return dfs(grid,i,j);
            }
        }
        return 0;
    }
};

?总结

图论题目主要是运用两种方法，深度优先遍历、广度优先遍历，本文章的三道题所用的均是深度优先遍历。