(2017|NIPS,VQ-VAE,离散潜在)神经离散表示学习
Neural Discrete Representation Learning
公和众和号:EDPJ(添加 VX:CV_EDPJ 或直接进 Q 交流群:922230617 获取资料)
目录
0. 摘要
学习在无监督情况下获取有用的表示仍然是机器学习中的一个关键挑战。在本文中,我们提出了一个简单而强大的生成模型,该模型学习离散表示。我们的模型,矢量量化变分自动编码器(Vector Quantised-Variational AutoEncoder,VQ-VAE),与 VAEs 有两个关键区别:编码器网络输出离散的编码,而不是连续的编码;先验是学习的,而不是静态的。为了学习离散潜在表示,我们结合了矢量量化(VQ)的思想。使用 VQ 方法可以使模型规避 “后验崩溃” 的问题,即在 VAE 框架中通常观察到的潜在变量在与强大的自回归解码器配对时会被忽略。将这些表示与自回归先验配对,模型可以生成高质量的图像、视频和语音,以及进行高质量的说话人转换和无监督的音素学习,进一步证明了学到的表示的实用性。
3. VQ-VAE
也许与我们方法最相关的工作是 VAEs。VAEs 包括以下部分: 一个编码器网络,该网络参数化给定输入数据 x 的离散潜在随机变量 z 的后验分布 q(z|x),一个先验分布 p(z),以及一个具有分布p(x|z) 的解码器。
通常,VAEs 中的后验和先验被假定为具有对角协方差的正态分布,这允许使用高斯重新参数化技巧 [32, 23]。扩展包括自回归先验和后验模型 [14]、归一化流 [31, 10] 以及逆自回归后验 [22]。
在这项工作中,我们引入了 VQ-VAE,其中我们使用具有新的训练方式的离散潜在变量,灵感来自矢量量化(VQ)。后验和先验分布是分类的,并且从这些分布中抽取的样本索引一个嵌入表。然后将这些嵌入用作解码器网络的输入。

3.1 离散潜在变量
我们定义一个潜在嵌入空间 e ∈ ?^(K × D),其中 K 是离散潜在空间的大小(即,K-way 分类),D 是每个潜在嵌入向量 e_i 的维度。请注意,有 K 个嵌入向量 e_i ∈ ?^D,i ∈ 1; 2; ...; K。如图 1 所示,
- 模型接收一个输入 x,通过编码器生成输出 z_e(x)。
- 然后,通过在共享的嵌入空间 e 中使用最近邻查找,计算离散潜在变量 z,如方程 1 所示。
- 解码器的输入是相应的嵌入向量 e_k,如方程 2 所示。
可以将这个正向计算流程视为具有将潜在变量映射到 K 个嵌入向量中的一个的特定非线性的常规自动编码器。模型的参数的完整集合是编码器、解码器和嵌入空间 e 的参数的并集。为简单起见,在本节中,我们使用一个随机变量 z 表示离散潜在变量,然而对于语音、图像和视频,我们分别提取 1D、2D 和 3D 潜在特征空间。
后验分类分布 q(z|x) 的概率被定义为 one-hot,如下所示:

其中 z_e(x) 是编码器网络的输出。我们将这个模型视为一个 VAE,我们可以用 ELBO 来限制 log p(x)。我们的提议分布 q(z = k|x) 是确定性的,通过在 z 上定义一个简单的均匀先验,我们得到一个 KL 散度常数,等于 logK。
表示 z_e(x) 经过离散化瓶颈,然后映射到嵌入 e 的最近元素,如方程 1 和 2 所示。
![]()
3.2 学习
请注意,对于方程 2,并没有定义真正的梯度,然而我们使用类似于直通估计器 [3] 的方法来近似梯度,并将梯度从解码器输入 z_q(x) 复制到编码器输出 z_e(x)。也可以通过量化操作的子梯度来进行估计,但这个简单的估计器在本文的初始实验中表现良好。?
在正向计算过程中,最近的嵌入 z_q(x)(方程 2)传递给解码器,在反向传播过程中,梯度 ▽_z L 未经修改地传递给编码器。由于编码器的输出表示和解码器的输入共享相同的 D 维空间,梯度包含了有关编码器如何改变其输出以降低重建损失的有用信息。

如图1(右)所示,梯度可以推动编码器的输出在下一个正向传递中以不同的方式进行离散化,因为方程 1 中的赋值将是不同的。
方程 3 指定了总体损失函数。它有三个组成部分,用于训练 VQ-VAE 的不同部分。第一项是重建损失(或数据项),它优化解码器和编码器(通过上面解释的估计器)。由于从 z_e(x) 映射到 z_q(x) 的直通梯度估计,嵌入 e_i 不接收来自重建损失 log p(z|z_q(x)) 的梯度。因此,为了学习嵌入空间,我们使用最简单的字典学习算法之一,矢量量化(VQ)。VQ 目标使用 𝑙_2 误差将嵌入向量 e_i 移向编码器输出 z_e(x),如方程 3 的第二项所示。由于这个损失项仅用于更新字典,因此还可以根据 z_e(x) 的移动平均更新字典项(在本文的实验中未使用)。有关更多详细信息,请参见附录 A.1。
最后,由于嵌入空间的体积是无维度的,如果嵌入 e_i 的训练速度不及编码器参数快,它可以任意增长。为了确保编码器致力于一个嵌入并且其输出不增长,我们添加了一个承诺损失(commitment loss),即方程 3 中的第三项。因此,总训练目标变为:
![]()
其中 sg 代表 stopgradient 运算符,该运算符在正向计算时定义为恒等,并且偏导数为零,因此有效地将其操作数约束为未更新的常数。解码器仅优化第一个损失项,编码器优化第一个和最后一个损失项,而嵌入由中间损失项优化。我们发现该算法对于 β 非常稳健,因为在 β 的值从 0.1 到 2.0 的范围内,结果并未发生变化。在所有实验中,我们使用 β = 0.25,尽管通常这取决于重建损失的尺度。 由于我们假设 z 的先验分布是均匀的,通常出现在 ELBO 中的 KL 项对于编码器参数是常数,因此在训练中可以忽略。
在我们的实验中,我们定义了 N 个离散潜在变量(例如,我们在 ImageNet 中使用了一个 32x32 的潜在变量域,或在 CIFAR10 中使用了一个 8x8x10 的潜在变量域)。得到的损失 L 是相同的,只是对于(每个潜在变量一个的) k-means 和承诺损失,我们得到了 N 个项的平均值。
完整模型的对数似然 log p(x) 可以如下评估:
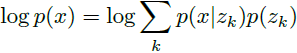
由于解码器 p(x|z) 是使用来自 MAP 推理的 z = z_q(x) 进行训练的,一旦它完全收敛,当 z ≠ z_q(x) 时,解码器就不应该分配任何概率质量给 p(x|z)。因此,我们可以写成
![]()
我们在第 4 节中通过实证评估了这个近似。根据 Jensen's 不等式,我们还可以写成
![]()
3.3 先验
离散潜在变量上的先验分布 p(z) 是一个类别分布,并且可以通过依赖于特征映射中的其他 z 来使其成为自回归的。在训练 VQ-VAE 时,先验保持恒定且均匀。训练后,我们拟合了一个关于 z 的自回归分布 p(z),以便通过祖先抽样(ancestral sampling)生成 x。对于图像,我们使用离散潜在变量的 PixelCNN,对于原始音频,我们使用 WaveNet。共同训练先验和 VQ-VAE,这可能会增强我们的结果,这留作未来的研究。
4. 实验

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 08 2024考研408-数据结构 第八章-排序学习笔记
- 【LeetCode:LCR 143. 子结构判断 | 二叉树 + 递归】
- CTF-PWN-栈溢出-中级ROP-【BROP-2】
- QEMU源码全解析 —— PCI设备模拟(5)
- 新式原子反应-蓝桥
- [Java][IOstream][转化流]以GBK读取数据用UTF-8写出数据的实例分析
- 【Redis】非关系型数据库之Redis的增删改查
- 复试 || 就业day06(2024.01.01)算法篇
- loki etcd
- postman进阶使用