KMeans clustering如何验证K点最佳 - silhouette analysis
发布时间:2024年01月12日
目录
二、Distortion Score Elbow for KMeans Clustering
?介绍:
Silhouette analysis是一种聚类分析的方法,用于评估数据点在聚类结果中的分离程度。它根据每个数据点与其所属聚类的内部距离和与其他聚类的外部距离之间的比值,计算出一个介于-1和1之间的Silhouette系数。
Silhouette系数越接近1,表示数据点与其所属聚类的内部距离较小,与其他聚类的外部距离较大,说明聚类有效。而Silhouette系数越接近-1,表示数据点与其所属聚类的内部距离较大,与其他聚类的外部距离较小,说明聚类结果不准确。如果Silhouette系数接近0,则表示数据点在边界附近,聚类结果模糊不清。
通过对所有数据点的Silhouette系数进行平均,可以得到一个聚类的整体Silhouette系数,用于评估聚类的质量。较高的Silhouette系数表示聚类结果更好,数据点更好地被正确分配到相应的聚类中。
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
# Generating the sample data from make_blobs
# This particular setting has one distinct cluster and 3 clusters placed close
# together.
X, y = make_blobs(n_samples=500,
n_features=2,
centers=4,
cluster_std=1,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1) # For reproducibility
range_n_clusters = [2, 3, 4, 5, 6]?一、The Elbow Method
from sklearn.cluster import KMeans
wcss=[]
for i in range(1,11):
kmeans=KMeans(n_clusters=i, init='k-means++',random_state=0)
kmeans.fit(X)
wcss.append(kmeans.inertia_)
plt.plot(range(1,11),wcss)
plt.title('The Elbow Method')
plt.xlabel('Number of Clusters')
plt.ylabel('WCSS')
plt.show()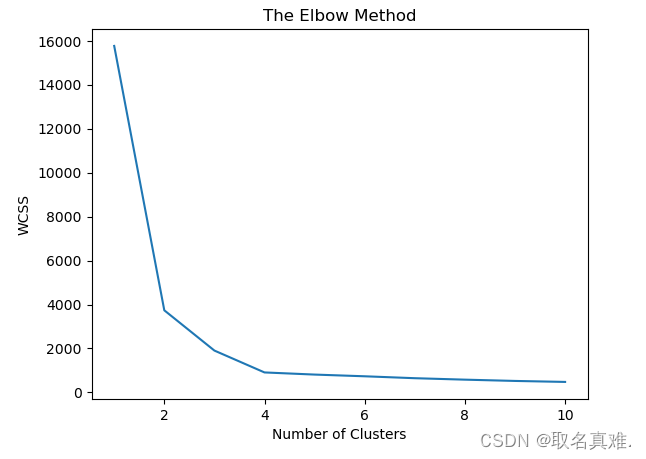
二、Distortion Score Elbow for KMeans Clustering
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from yellowbrick.cluster import KElbowVisualizer
model_ori = KMeans()
visualizer = KElbowVisualizer(model_ori, k = (1, 11)) #k = 1 to 11
visualizer.fit(X)
visualizer.show()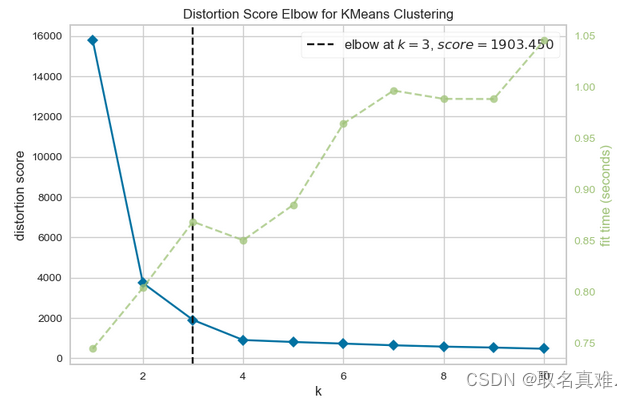
三、?silhouette analysis
'''from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
print(__doc__)
# Generating the sample data from make_blobs
# This particular setting has one distinct cluster and 3 clusters placed close
# together.
X, y = make_blobs(n_samples=500,
n_features=2,
centers=4,
cluster_std=1,
center_box=(-10.0, 10.0),
shuffle=True,
random_state=1) # For reproducibility
range_n_clusters = [2, 3, 4, 5, 6]
'''
for n_clusters in range_n_clusters:
# Create a subplot with 1 row and 2 columns
fig, (ax1, ax2) = plt.subplots(1, 2)
fig.set_size_inches(18, 7)
# The 1st subplot is the silhouette plot
# The silhouette coefficient can range from -1, 1 but in this example all
# lie within [-0.1, 1]
ax1.set_xlim([-0.1, 1])
# The (n_clusters+1)*10 is for inserting blank space between silhouette
# plots of individual clusters, to demarcate them clearly.
ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])
# Initialize the clusterer with n_clusters value and a random generator
# seed of 10 for reproducibility.
clusterer = KMeans(n_clusters=n_clusters, random_state=10)
cluster_labels = clusterer.fit_predict(X)
# The silhouette_score gives the average value for all the samples.
# This gives a perspective into the density and separation of the formed
# clusters
silhouette_avg = silhouette_score(X, cluster_labels)
print("For n_clusters =", n_clusters,
"The average silhouette_score is :", silhouette_avg)
# Compute the silhouette scores for each sample
sample_silhouette_values = silhouette_samples(X, cluster_labels)
y_lower = 10
for i in range(n_clusters):
# Aggregate the silhouette scores for samples belonging to
# cluster i, and sort them
ith_cluster_silhouette_values = \
sample_silhouette_values[cluster_labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i) / n_clusters)
ax1.fill_betweenx(np.arange(y_lower, y_upper),
0, ith_cluster_silhouette_values,
facecolor=color, edgecolor=color, alpha=0.7)
# Label the silhouette plots with their cluster numbers at the middle
ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
# Compute the new y_lower for next plot
y_lower = y_upper + 10 # 10 for the 0 samples
ax1.set_title("The silhouette plot for the various clusters.")
ax1.set_xlabel("The silhouette coefficient values")
ax1.set_ylabel("Cluster label")
# The vertical line for average silhouette score of all the values
ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
ax1.set_yticks([]) # Clear the yaxis labels / ticks
ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
# 2nd Plot showing the actual clusters formed
colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
ax2.scatter(X[:, 0], X[:, 1], marker='.', s=30, lw=0, alpha=0.7,
c=colors, edgecolor='k')
# Labeling the clusters
centers = clusterer.cluster_centers_
# Draw white circles at cluster centers
ax2.scatter(centers[:, 0], centers[:, 1], marker='o',
c="white", alpha=1, s=200, edgecolor='k')
for i, c in enumerate(centers):
ax2.scatter(c[0], c[1], marker='$%d$' % i, alpha=1,
s=50, edgecolor='k')
ax2.set_title("The visualization of the clustered data.")
ax2.set_xlabel("Feature space for the 1st feature")
ax2.set_ylabel("Feature space for the 2nd feature")
plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
"with n_clusters = %d" % n_clusters),
fontsize=14, fontweight='bold')
plt.show()#k等于4时 分布较为平均 选取4

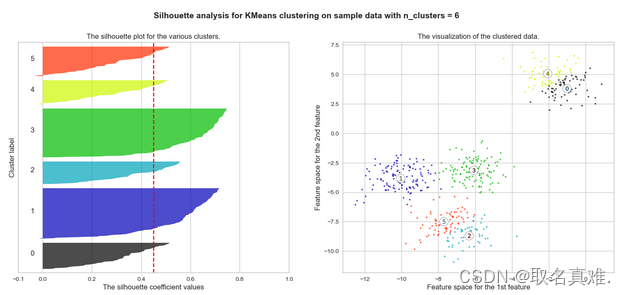
文章来源:https://blog.csdn.net/qq_74156152/article/details/135544211
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 免 费 搭 建 小程序商城,打造多商家入驻的b2b2c、o2o、直播带货商城
- Python3条件控制
- 【网络安全 | Misc】miss_01 太湖杯
- geemap学习笔记041:Landsat Collection2系列数据去云算法总结
- HarmonyOS 开发实例—蜜蜂 AI 助手
- 常用冷凝器的传热系数与单位换热面积推荐数据
- 【Kimi帮我读论文】《LlaMaVAE: Guiding Large Language Model Generation via Continuous Latent Sentence Spaces》
- 动态SQL:MyBatis强大的特性之一
- Latex + Overleaf 论文写作新手笔记
- 病理HE学习贴(自备)