虚数的本质 2024年1月18日11:01:48

发布时间：2024年01月18日

虚数的本质
高中物理主要学习牛顿力学，牛顿都觉得虚数没有意义，高中生更加认为也没有意义了。
20世纪下半叶开始，虚数成了物理学家和数学家必备的技能，量子力学/信号处理都会用到。
文艺复兴期间，卡尔达诺《大术》中给出了解三次方程的一般形式。
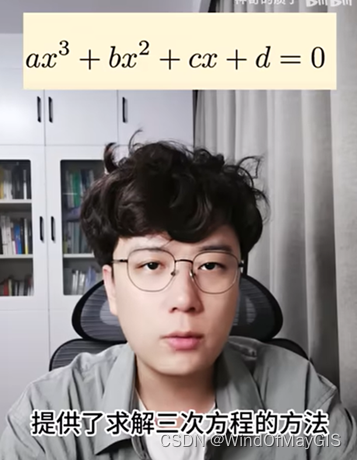
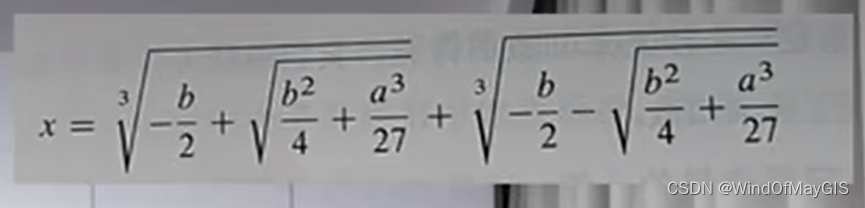
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

这是数学跨越千年的一个重大突破。但存在这样的问题，应用于以下式子会存在问题
在这里插入图片描述

后来邦贝利发现了解4，如果忽略负数开根号就可以了。
在这里插入图片描述

答案是4.
虚构出来的数，属于存在与非存在之间的两栖动物（莱布尼茨）。
后来将x+iy表示为平面上的点
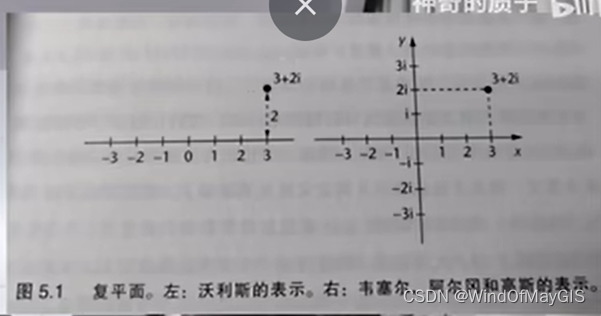
在这里插入图片描述

这种几何表示，很不错，但是没有解释为什么复数可以表示出逻辑自洽的数系？
后来是因为虚数好用，才不去关注虚数的本质。
复数加法是矢量叠加的过程。
复数的乘法是旋转的过程。
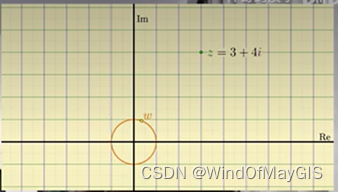
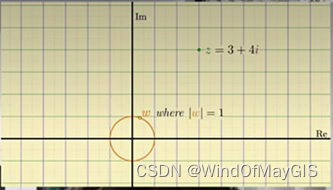
在这里插入图片描述
在这里插入图片描述

乘以复数w，
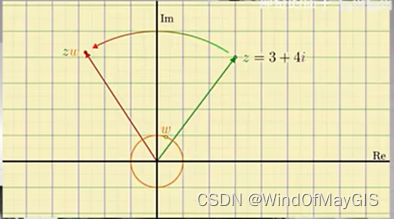
在这里插入图片描述

相乘之后的结果等于Z旋转了一个角度，角度是多少？？？？。
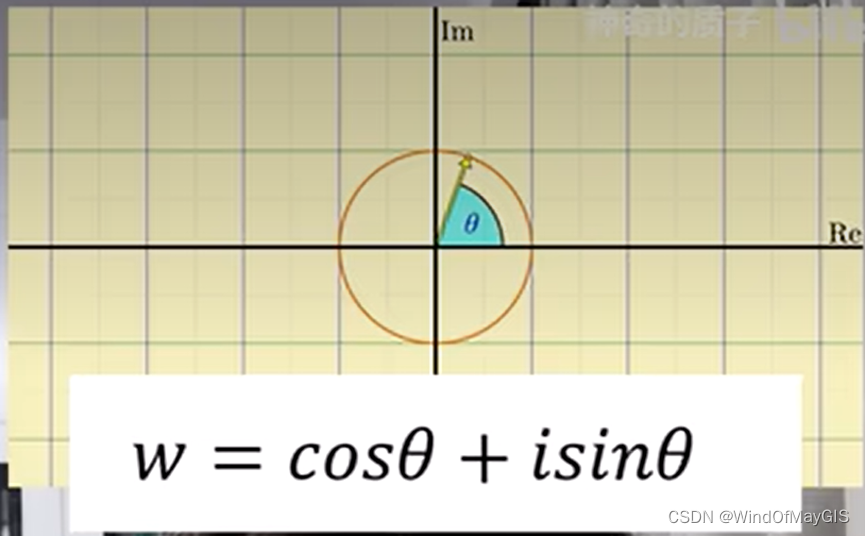
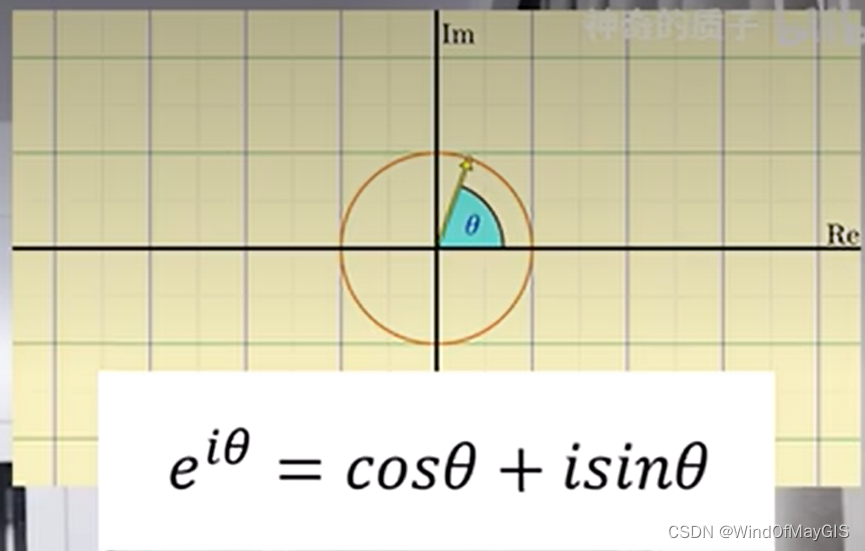
在这里插入图片描述
在这里插入图片描述

欧拉公式
泰勒级数，三角函数展开成幂级数
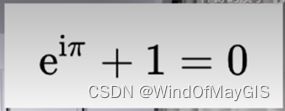
在这里插入图片描述

哈密顿给出了复数的最终解释：运算规则的巧妙选择，使得其如此好用。
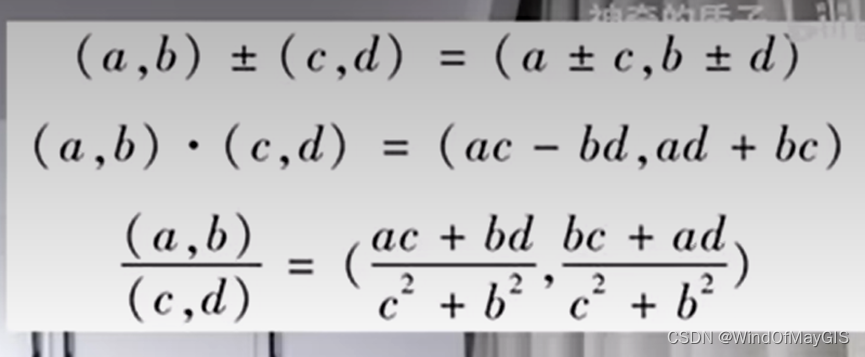
在这里插入图片描述

复变函数？？？？

参考：https://www.bilibili.com/video/BV1Am4y1i7rX/?spm_id_from=333.337.search-card.all.click&vd_source=cb328c0100091e8200a9baf5f3afbf04

文章来源:https://blog.csdn.net/zhouxinxin111/article/details/135668996
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
最新文章