Codeforces Hello 2024 （ABCDF1题）

A. Wallet Exchange

Problem Statement

Alice and Bob are bored, so they decide to play a game with their wallets. Alice has $a$ coins in her wallet, while Bob has $b$ coins in his wallet.

Both players take turns playing, with Alice making the first move. In each turn, the player will perform the following steps in order:

1. Choose to exchange wallets with their opponent, or to keep their current wallets.
2. Remove $1$ coin from the player’s current wallet. The current wallet cannot have $0$ coins before performing this step.

The player who cannot make a valid move on their turn loses. If both Alice and Bob play optimally, determine who will win the game.

Input

Each test contains multiple test cases. The first line contains a single integer $t$ ($1\le t\le 1000$) — the number of test cases. The description of the test cases follows.

The first and only line of each test case contains two integers $a$ and $b$ ($1\le a,b\le 10^9$) — the number of coins in Alice’s and Bob’s wallets, respectively.

Output

For each test case, output “Alice” if Alice will win the game, and “Bob” if Bob will win the game.

Example

input
10
1 1
1 4
5 3
4 5
11 9
83 91
1032 9307
839204 7281
1000000000 1000000000
53110 2024

output
Bob
Alice
Bob
Alice
Bob
Bob
Alice
Alice
Bob
Bob

Note

In the first test case, an example of the game is shown below:

• Alice chooses to not swap wallets with Bob in step 1 of her move. Now, $a=0$ and $b=1$.
• Since Alice’s wallet is empty, Bob must choose to not swap their wallets in step 1 of his move. Now, $a=0$ and $b=0$.
• Since both Alice’s and Bob’s wallets are empty, Alice is unable to make a move. Hence, Bob wins.

In the second test case, an example of the game is shown below:

• Alice chooses to swap wallets with Bob in step 1 of her move. Now, $a=3$ and $b=1$.
• Bob chooses to swap wallets with Alice in step 1 of his move. Now, $a=1$ and $b=2$.
• Alice chooses to not swap wallets with Bob in step 1 of her move. Now, $a=0$ and $b=2$.
• Since Alice’s wallet is empty, Bob can only choose to not swap wallets with Alice in step 1 of his move. Now, $a=0$ and $b=1$.
• Since Alice’s wallet is empty, Alice can only choose to swap wallets with Bob in step 1 of her move. Now, $a=0$ and $b=0$.
• Since both Alice’s wallet and Bob’s wallet are empty, Bob is unable to make a move. Hence, Alice wins.

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef pair<int, int> PII;

void solve()
{
	int A, B;

	cin >> A >> B;

	if (abs(A - B) & 1) cout << "Alice" << endl;
	else cout << "Bob" << endl;
}

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int Data;

	cin >> Data;

	while (Data --)
		solve();

	return 0;
}

B. Plus-Minus Split

Problem Statement

You are given a string $s$ of length $n$ consisting of characters “+” and “-”. $s$ represents an array $a$ of length $n$ defined by $a_i=1$ if $s_i=$ “+” and $a_i=?1$ if $s_i=$ “-”.

You will do the following process to calculate your penalty:

1. Split $a$ into non-empty arrays $b_1,b_2,\dots ,b_k$ such that $b_1+b_2+\dots +b_k=a^{?}$, where $+$ denotes array concatenation.
2. The penalty of a single array is the absolute value of its sum multiplied by its length. In other words, for some array $c$ of length $m$, its penalty is calculated as $p(c)=|c_1+c_2+\dots +c_m|?m$.
3. The total penalty that you will receive is $p(b_1)+p(b_2)+\dots +p(b_k)$.

If you perform the above process optimally, find the minimum possible penalty you will receive.

${}^{?}$ Some valid ways to split $a=[3,1,4,1,5]$ into $(b_1,b_2,\dots ,b_k)$ are $([3],[1],[4],[1],[5])$, $([3,1],[4,1,5])$ and $([3,1,4,1,5])$ while some invalid ways to split $a$ are $([3,1],[1,5])$, $([3],[],[1,4],[1,5])$ and $([3,4],[5,1,1])$.

Input

Each test contains multiple test cases. The first line contains a single integer $t$ ($1\le t\le 1000$) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer $n$ ($1\le n\le 5000$) — the length of string $s$.

The second line of each test case contains string $s$ ( s i ∈ { + , ? } s_i \in \{ \mathtt{+}, \mathtt{-} \} si?∈{+,?}, $|s|=n$).

Note that there are no constraints on the sum of $n$ over all test cases.

Output

For each test case, output a single integer representing the minimum possible penalty you will receive.

Example

input
5
1
+
5
-----
6
+-+-+-
10
--+++++++-
20
+---++++-+++++---++-

output
1
5
0
4
4

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef pair<int, int> PII;

const int SIZE = 5e3 + 10;

int N;
string S;

void solve()
{
	cin >> N >> S;

	S = ' ' + S;
	int Result = 0;
	for (int i = 1; i <= N; i ++)
		if (S[i] == '+')
			Result ++;
		else
			Result --;

	cout << abs(Result) << endl;
}

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int Data;

	cin >> Data;

	while (Data --)
		solve();

	return 0;
}

C. Grouping Increases

Problem Statement

You are given an array $a$ of size $n$. You will do the following process to calculate your penalty:

1. Split array $a$ into two (possibly empty) subsequences${}^{?}$ $s$ and $t$ such that every element of $a$ is either in $s$ or $t^{?}$.
2. For an array $b$ of size $m$, define the penalty $p(b)$ of an array $b$ as the number of indices $i$ between $1$ and $m?1$ where $b_i<b_{i+1}$.
3. The total penalty you will receive is $p(s)+p(t)$.

If you perform the above process optimally, find the minimum possible penalty you will receive.

${}^{?}$ A sequence $x$ is a subsequence of a sequence $y$ if $x$ can be obtained from $y$ by the deletion of several (possibly, zero or all) elements.

${}^{?}$ Some valid ways to split array $a=[3,1,4,1,5]$ into $(s,t)$ are $([3,4,1,5],[1])$, $([1,1],[3,4,5])$ and $([],[3,1,4,1,5])$ while some invalid ways to split $a$ are $([3,4,5],[1])$, $([3,1,4,1],[1,5])$ and $([1,3,4],[5,1])$.

Input

Each test contains multiple test cases. The first line contains a single integer $t$ ($1\le t\le 10^4$) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer $n$ ($1\le n\le 2?10^5$) — the size of the array $a$.

The second line contains $n$ integers $a_1,a_2,\dots ,a_n$ ($1\le a_i\le n$) — the elements of the array $a$.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2?10^5$.

Output

For each test case, output a single integer representing the minimum possible penalty you will receive.

Example

input
5
1
+
5
-----
6
+-+-+-
10
--+++++++-
20
+---++++-+++++---++-

output
3
1
0
0
0

Note

In the first test case, a possible way to split $a$ is $s=[2,4,5]$ and $t=[1,3]$. The penalty is $p(s)+p(t)=2+1=3$.

In the second test case, a possible way to split $a$ is $s=[8,3,1]$ and $t=[2,1,7,4,3]$. The penalty is $p(s)+p(t)=0+1=1$.

In the third test case, a possible way to split $a$ is $s=[]$ and $t=[3,3,3,3,3]$. The penalty is $p(s)+p(t)=0+0=0$.

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef pair<int, int> PII;

const int SIZE = 2e5 + 10;

int N;
int A[SIZE];

void solve()
{
    cin >> N;

    for (int i = 1; i <= N; i ++)
        cin >> A[i];

    std::vector<int> S1, S2;
    S1.push_back(1e18), S2.push_back(1e18);

    for (int i = 1; i <= N; i ++)
        if (A[i] > S1.back() && A[i] > S2.back())
        {
            if (S1.back() < S2.back()) S1.push_back(A[i]);
            else S2.push_back(A[i]);
        }
        else if (A[i] > S1.back() && A[i] <= S2.back())
            S2.push_back(A[i]);
        else if (A[i] <= S1.back() && A[i] > S2.back())
            S1.push_back(A[i]);
        else
        {
            if (S1.back() < S2.back()) S1.push_back(A[i]);
            else S2.push_back(A[i]);
        }

    int Result = 0;
    for (int i = 1; i < (int)S1.size(); i ++)
        Result += (S1[i] > S1[i - 1]);
    for (int i = 1; i < (int)S2.size(); i ++)
        Result += (S2[i] > S2[i - 1]);

    cout << Result << endl;
}

signed main()
{
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);

    int Data;

    cin >> Data;

    while (Data --)
        solve();

    return 0;
}

D. 01 Tree

Problem Statement

There is an edge-weighted complete binary tree with $n$ leaves. A complete binary tree is defined as a tree where every non-leaf vertex has exactly 2 children. For each non-leaf vertex, we label one of its children as the left child and the other as the right child.

The binary tree has a very strange property. For every non-leaf vertex, one of the edges to its children has weight $0$ while the other edge has weight $1$. Note that the edge with weight $0$ can be connected to either its left or right child.

You forgot what the tree looks like, but luckily, you still remember some information about the leaves in the form of an array $a$ of size $n$. For each $i$ from $1$ to $n$, $a_i$ represents the distance${}^{?}$ from the root to the $i$-th leaf in dfs order${}^{?}$. Determine whether there exists a complete binary tree which satisfies array $a$. Note that you do not need to reconstruct the tree.

${}^{?}$ The distance from vertex $u$ to vertex $v$ is defined as the sum of weights of the edges on the path from vertex $u$ to vertex $v$.

${}^{?}$ The dfs order of the leaves is found by calling the following $\text{dfs}$ function on the root of the binary tree.

dfs_order = []

function dfs(v):
if v is leaf:
append v to the back of dfs_order
else:
dfs(left child of v)
dfs(right child of v)

dfs(root)

Input

Each test contains multiple test cases. The first line contains a single integer $t$ ($1\le t\le 10^4$) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer $n$ ($2\le n\le 2?10^5$) — the size of array $a$.

The second line of each test case contains $n$ integers $a_1,a_2,\dots ,a_n$ ($0\le a_i\le n?1$) — the distance from the root to the $i$-th leaf.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2?10^5$.

Output

For each test case, print “YES” if there exists a complete binary tree which satisfies array $a$ and “NO” otherwise.

You may print each letter in any case (for example, “YES”, “Yes”, “yes”, “yEs” will all be recognized as a positive answer).

Example

input
2
5
2 1 0 1 1
5
1 0 2 1 3

output
YES
NO

Note

In the first test case, the following tree satisfies the array.

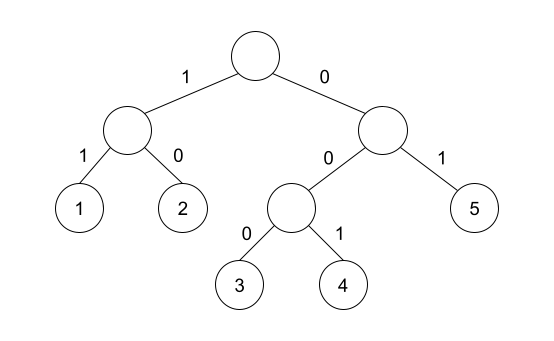
In the second test case, it can be proven that there is no complete binary tree that satisfies the array.

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef pair<int, int> PII;

const int SIZE = 2e5 + 10;

int N;
int A[SIZE], Next[SIZE], Prev[SIZE];
int Vis[SIZE];

bool Del(int X)
{
	if (X < 1 || X > N) return 0;
	return A[Prev[X]] + 1 == A[X] || A[Next[X]] + 1 == A[X];
}

void solve()
{
	cin >> N;

	for (int i = 1; i <= N; i ++)
		cin >> A[i];

	priority_queue<PII> Heap;
	for (int i = 1; i <= N; i ++)
		Next[i] = i + 1, Prev[i] = i - 1, Vis[i] = 0;

	A[0] = -1e18, A[N + 1] = -1e18;
	for (int i = 1; i <= N; i ++)
		if (Del(i))
			Heap.push({A[i], i}), Vis[i] = 1;

	while (Heap.size())
	{
		auto T = Heap.top();
		Heap.pop();

		int u = T.second;
		Next[Prev[u]] = Next[u], Prev[Next[u]] = Prev[u];
		if (!Vis[Next[u]] && Del(Next[u]))
			Vis[Next[u]] = 1, Heap.push({A[Next[u]], Next[u]});
		if (!Vis[Prev[u]] && Del(Prev[u]))
			Vis[Prev[u]] = 1, Heap.push({A[Prev[u]], Prev[u]});
	}

	int Cnt = 0, Min = 1e18;
	for (int i = 1; i <= N; i ++)
		Cnt += !Vis[i], Min = min(Min, A[i]);

	if (Cnt == 1 && Min == 0) puts("YES");
	else puts("NO");
}

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int Data;

	cin >> Data;

	while (Data --)
		solve();

	return 0;
}

F1. Wine Factory (Easy Version)

Problem Statement

This is the easy version of the problem. The only difference between the two versions is the constraint on $c_i$ and $z$. You can make hacks only if both versions of the problem are solved.

There are three arrays $a$, $b$ and $c$. $a$ and $b$ have length $n$ and $c$ has length $n?1$. Let $W(a,b,c)$ denote the liters of wine created from the following process.

Create $n$ water towers. The $i$-th water tower initially has $a_i$ liters of water and has a wizard with power $b_i$ in front of it. Furthermore, for each $1\le i\le n?1$, there is a valve connecting water tower $i$ to $i+1$ with capacity $c_i$.

For each $i$ from $1$ to $n$ in this order, the following happens:

1. The wizard in front of water tower $i$ removes at most $b_i$ liters of water from the tower and turns the removed water into wine.
2. If $i\ne n$, at most $c_i$ liters of the remaining water left in water tower $i$ flows through the valve into water tower $i+1$.

There are $q$ updates. In each update, you will be given integers $p$, $x$, $y$ and $z$ and you will update $a_p:=x$, $b_p:=y$ and $c_p:=z$. After each update, find the value of $W(a,b,c)$. Note that previous updates to arrays $a$, $b$ and $c$ persist throughout future updates.

Input

The first line contains two integers $n$ and $q$ ($2\le n\le 5?10^5$, $1\le q\le 5?10^5$) — the number of water towers and the number of updates.

The second line contains $n$ integers $a_1,a_2,\dots ,a_n$ ($0\le a_i\le 10^9$) — the number of liters of water in water tower $i$.

The third line contains $n$ integers $b_1,b_2,\dots ,b_n$ ($0\le b_i\le 10^9$) — the power of the wizard in front of water tower $i$.

The fourth line contains $n?1$ integers $c_1,c_2,\dots ,c_{n?1}$ ($c_i=10^{18}$) — the capacity of the pipe connecting water tower $i$ to $i+1$.

Each of the next $q$ lines contains four integers $p$, $x$, $y$ and $z$ ($1\le p\le n$, $0\le x,y\le 10^9$, $z=10^{18}$) — the updates done to arrays $a$, $b$ and $c$.

Note that $c_n$ does not exist, so the value of $z$ does not matter when $p=n$.

Output

Print $q$ lines, each line containing a single integer representing $W(a,b,c)$ after each update.

Example

input
4 3
3 3 3 3
1 4 2 8
1000000000000000000 1000000000000000000 1000000000000000000
4 3 8 1000000000000000000
2 5 1 1000000000000000000
3 0 0 1000000000000000000

output
12
12
10

input
5 5
10 3 8 9 2
3 4 10 8 1
1000000000000000000 1000000000000000000 1000000000000000000 1000000000000000000
5 4 9 1000000000000000000
1 1 1 1000000000000000000
2 7 4 1000000000000000000
4 1 1 1000000000000000000
1 8 3 1000000000000000000

output
34
25
29
21
27

Solution

具体见文后视频。

---

Code

#include <bits/stdc++.h>
#define lowbit(x) x & -x
#define int long long

using namespace std;

typedef pair<int, int> PII;

const int SIZE = 5e5 + 10;

int N, Q;
int A[SIZE], B[SIZE], Pre[SIZE];
struct Segment
{
	int l, r;
	int Max, Id, Lazy;
}Tree[SIZE << 2];
struct Fenwick
{
	int Tree[SIZE];
	Fenwick() { memset(Tree, 0, sizeof Tree); }
	void Add(int x, int d) { for (int i = x; i <= N; i += lowbit(i)) Tree[i] += d; }
	int Sum(int x)
	{
		int Result = 0;
		for (int i = x; i; i -= lowbit(i))
			Result += Tree[i];
		return Result;
	}
}SA, SB;

void Pushup(int u)
{
	if (Tree[u << 1].Max > Tree[u << 1 | 1].Max) Tree[u].Id = Tree[u << 1].Id, Tree[u].Max = Tree[u << 1].Max;
	else Tree[u].Id = Tree[u << 1 | 1].Id, Tree[u].Max = Tree[u << 1 | 1].Max;
}

void Build(int u, int l, int r)
{
	if (l == r)
	{
		Tree[u] = {l, l, Pre[l], l};
		return;
	}

	Tree[u] = {l, r};
	int mid = l + r >> 1;
	Build(u << 1, l, mid), Build(u << 1 | 1, mid + 1, r);
	Pushup(u);
}

void Pushdown(int u)
{
	if (Tree[u].Lazy)
	{
		Tree[u << 1].Max += Tree[u].Lazy, Tree[u << 1].Lazy += Tree[u].Lazy;
		Tree[u << 1 | 1].Max += Tree[u].Lazy, Tree[u << 1 | 1].Lazy += Tree[u].Lazy;
		Tree[u].Lazy = 0;
	}
}

void Modify(int u, int l, int r, int d)
{
	if (Tree[u].l >= l && Tree[u].r <= r)
	{
		Tree[u].Max += d, Tree[u].Lazy += d;
		return;
	}

	Pushdown(u);
	int mid = Tree[u].l + Tree[u].r >> 1;
	if (mid >= l) Modify(u << 1, l, r, d);
	if (mid < r) Modify(u << 1 | 1, l, r, d);
	Pushup(u);
}

PII Query(int u, int l, int r)
{
	if (Tree[u].l >= l && Tree[u].r <= r)
		return {Tree[u].Max, Tree[u].Id};

	Pushdown(u);
	int mid = Tree[u].l + Tree[u].r >> 1;
	if (mid >= l && mid < r)
	{
		PII A = Query(u << 1, l, r), B = Query(u << 1 | 1, l, r), Result;
		if (A.first > B.first) Result.second = A.second, Result.first = A.first;
		else Result.second = B.second, Result.first = B.first;
		return Result;
	}
	else if (mid >= l) return Query(u << 1, l, r);
	else return Query(u << 1 | 1, l, r);
}

signed main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	cin >> N >> Q;

	for (int i = 1; i <= N; i ++)
		cin >> A[i], SA.Add(i, A[i]);
	for (int i = 1; i <= N; i ++)
		cin >> B[i], SB.Add(i, B[i]), Pre[i] = Pre[i - 1] + B[i] - A[i];
	int C;
	for (int i = 1; i < N; i ++)
		cin >> C;

	Build(1, 1, N);

	int P, X, Y, Z;
	while (Q --)
	{
		cin >> P >> X >> Y >> Z;

		Modify(1, P, N, (Y - X) - (B[P] - A[P]));
		SA.Add(P, X - A[P]), SB.Add(P, Y - B[P]);
		A[P] = X, B[P] = Y;

		auto T = Query(1, 1, N);
		int u = T.second, Max = T.first;

		if (Max <= 0)
			cout << SB.Sum(N) << endl;
		else
			cout << SA.Sum(u) + SB.Sum(N) - SB.Sum(u) << endl;
	}

	return 0;
}

视频题解

---

最后祝大家早日