条件风险价值CVaR内容介绍(MATLAB例程)

? ? ? ? 在对微电网优化调度过程中，由于新能源机组出力和负荷的不确定性，若采用确定性的优化调度方案会存在一定的风险。当风电和光伏输出功率的实际值低于预测值时，需要增加可控机组出力或切除部分负荷；反之，若风电和光伏输出功率的实际值高于预测值时，则需要降低可控机组出力或者弃风弃光，这都会给系统带来运行费用增加的风险。因此，在微电网优化调度中通常采用CVaR（Condition Value at Risk, CVaR）来量化微电网中的不确定性因素带来的风险成本。
????????CVaR是基于风险价值（Value at Risk, VaR）发展而来的，是在一定置信水平α下，损失超过VaR值时的条件均值[1]。VaR是指在一定的置信水平下，某一投资组合在未来某一时间段内的最大损失。假设是n维的决策向量，为m维决定系统风险损失的随机向量f(y)为y的概率密度函数。系统的损失函数为h(x,y)，则损失不超过某一估计值η的概率为：

????????给定置信水平，当时，η的最小值即为VaR值，即：

????????此时，条件风险价值CVaR的表达式为:

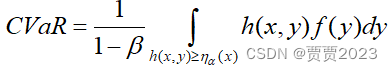
????????为了便于计算，引入辅助函数来计算CVaR的值[2]，即:

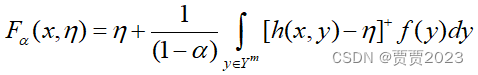
????????当随机变量y的概率分布解析表达式难以求取时，可以利用蒙特卡洛法来模拟样本数据，y1,y2,……,ym是y的m个样本，则CVaR的估计值为[3]：

式中，m为所有场景的数量，yk为第k个场景下随机变量的值，为第k个场景发生的概率。此时
的最小值即为CVaR，对应的即为VaR。
????????具体MATLAB编程可参考：条件风险价值CVaR例程(MATLAB实现)

参考文献

[1] Wei Zhinong, Chen Wei, Huang Wenjin, et al. Opitimal allocation model for multi-energy capacity of virtual power plant considering conditional value-at-risk[J]. Automation of Electric Power Sytems, 2018, 42(4): 39-46.

[2] Rockafellar R T, Uryasev S. Conditional value-at-risk for general loss distributions[J]. Journal of Banking and Finance, 2002, 26(7): 1443-1471.

[3] Liu Xingyu, Wen Buying, Jiang Yuewen. Study on rotary standby benefit of wind power system with conditional risk value[J]. Transactions of China Electrotechnical Society, 2017, 32(9): 169-178.