[Optimization] First Sight of Linear Optimization problem

Three main components in optimization problems

I Decision

I Objective

I Constraints

General form of optimization problem:

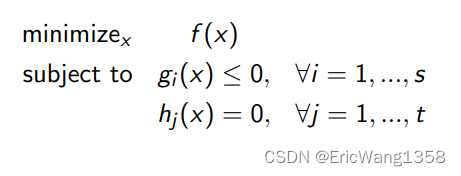
We have shown some examples of formulating a problem into optimization problem — maximum area problem, production planning problem, shortest path problem, vertex cover problem, support vector machine problem.

I Definition

A linear optimization problem, or a linear program (LP), is an optimization problem in which the objective function and all constraint functions are linear (in the decision variables).

A linear optimization problem can be generally written as

We can write LPs in a more compact way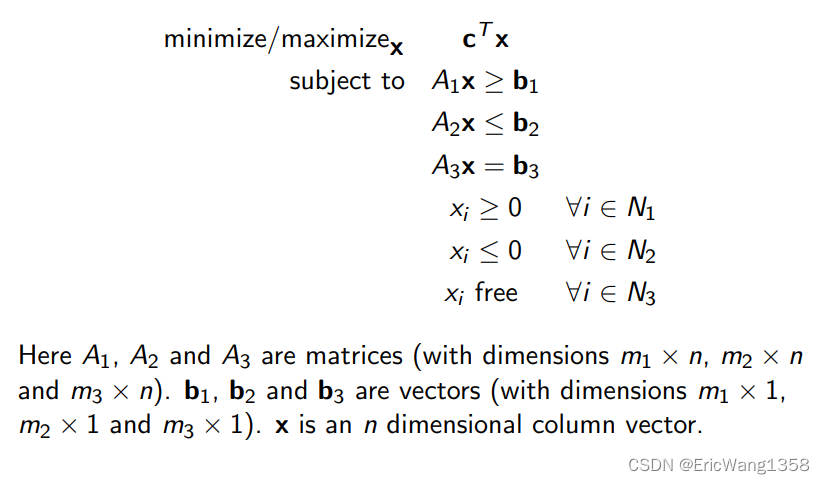

Linear optimization belongs to continuous optimization

I Standard form

In order to study it more systematically, we want to have a standard (and even more compact) form of LP. An LP is said to be of standard form if it is of the form: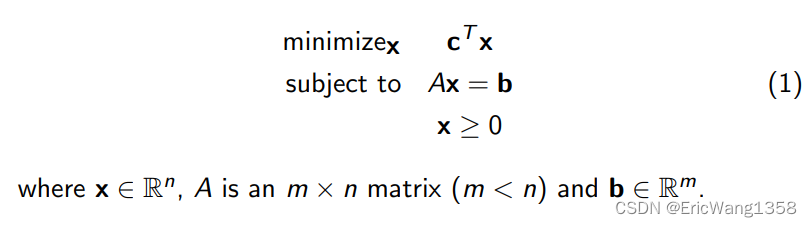In fact, any LP can be written in the standard form, using some “tricks”.

If the objective was maximization

????????I Use ?c instead of c and change it to minimization

Eliminating inequality constraints?Ax ≤ b or Ax ≥ b

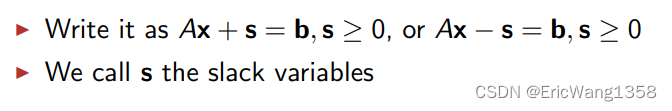notice that the equation about s is also linear, so we have a new slack variable?here.

If one has xi ≤ 0

????????I Define yi = ?xi

Eliminating “free” variables xi (no sign constraint on xi)

the decomposition of a variable xi? into two non-negative components

Standard form is mainly used for analysis purposes. We don’t need to write a problem in standard form unless necessary. Usually just write in a way that is easy to understand. However, being able to transform an LP into the standard form is an important skill. It is helpful for analyzing LP problems as well as using some software to solve it.

Some more examples

A hospital wants to make a weekly night shift schedule for its nurses

The demand for the night shift on day j is dj , for j = 1, ..., 7

Every nurse works 5 days in a row I We want to minimize the total number of nurses used while meeting all demand

Ignore the integrality constraints for now (i.e., we allow “half” nurse if necessary)

What is your choice of decision variable?

How about xi to be the number of nurses on day i?

Can’t capture the constraints that nurses have to work 5 days in a row

A better way is to define xi to be the number of nurses starting at day i

Our objective will be minimize x1 + x2 + x3 + x4 + x5 + x6 + x7

An air traffic controller needs to control the landing time of n aircrafts

I Flights must land in the order 1, ..., n

I Flight j must land in time interval [aj , bj ]

I The objective is to maximize the minimum separation time, which is the interval between two landings

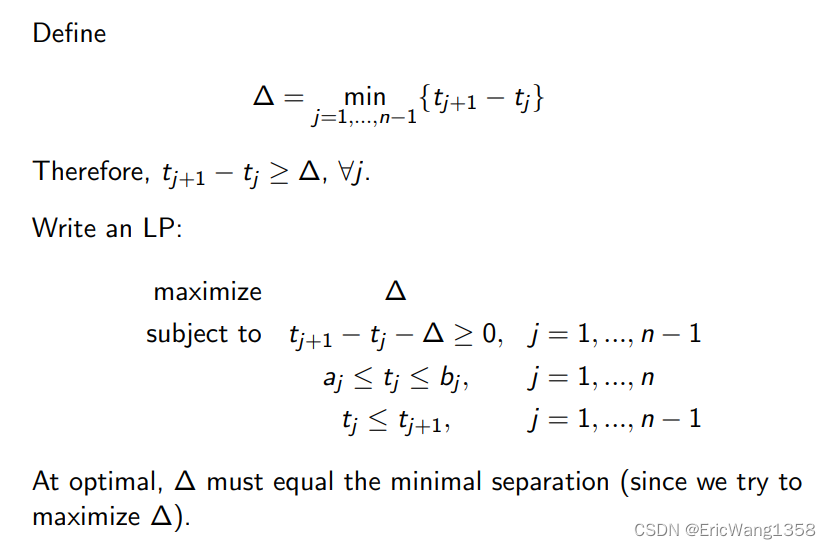
Why Linear Program?

Easiest to solve.

I Theoretically, it is polynomial time solvable, and the complexity is low among all optimization problems.

I Practically, commercial softwares can solve LPs with tens of thousands of variables very easily. Can solve LPs with millions of variables if there are some structures

Extremely versatile

I Can model many real problems, either exactly or approximately Fundamental

I The LP theories lay the foundation for most optimization theories