【数学建模】综合评价方法

综合评价的基本理论和数据预处理

一个综合评价问题是由评价对象、评价指标、权重系数、综合评价模型和评价者五个基本要素组成

综合评价的基本概念

评价对象：研究对象，同类多个，记作$S_1,S_2,...,S_n(n>1)$
评价指标：也称综合评价的指标体系，包含多个指标，用向量$x$表示，记作$x=[x_1,x_2,...,x_m]$
权重系数：刻画各个评价指标的相对重要性，用$w_j(j=1,2,...,m)$表示评价指标$j$的权重系数，满足$w_j\ge 0,j=1,2,...,m;且{\sum }_{j=1}^m{w}_j=1$
综合评价模型：实现将多个评价指标值综合得到一个整体的综合评价值，第$i$个评价对象的综合评价值$b_i$由评价指标$a_i=[a_{i1},a_{i2},...,a_{im}]$和权重向量$w=[w_1,w_2,...,w_m]$根据评价模型$y=f(x,w)$得到
评价者

综合评价体系的构建

综合评价过程包括评价指标体系的建立、评价指标的预处理、指标权重的确定和评价模型的选择等重要环节

评价指标和评价指标体系
从指标特征分为：定性指标和定量指标
从指标变化对评价目的的影响来看：极大型指标、极小型指标、剧中型指标和区间型指标

评价指标的筛选
专家调研法：查阅相关资料得到
最小均方差法：排除不重要的指标，不重要的指标指各个评价对象在该指标上的观测值都差不多，即是根据指标的差异程度进行判断

综合指标的预处理方法

消除不同指标间有关类型、单位、数量级等的差异，避免出现不合理的评价结果
对指标进行一致化处理、无量纲化处理

指标一致化处理
将非极大型指标转化为极大型指标
极小转极大：取倒转化$\dot{x_j}=\frac{1}{x_j}$、平移转化$\dot{x_j}=M_j?x_j$其中 M j = m a x 1 ≤ i ≤ n { a i j } M_j=max_{1\leq i \leq n}\{a_{ij}\} Mj?=max1≤i≤n?{aij?}
居中转极大：

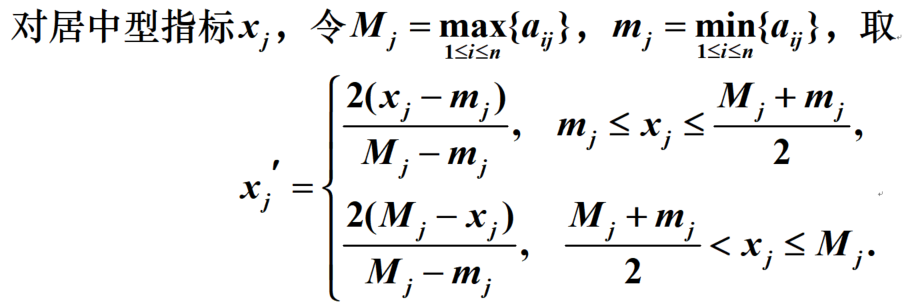
区间转极大：

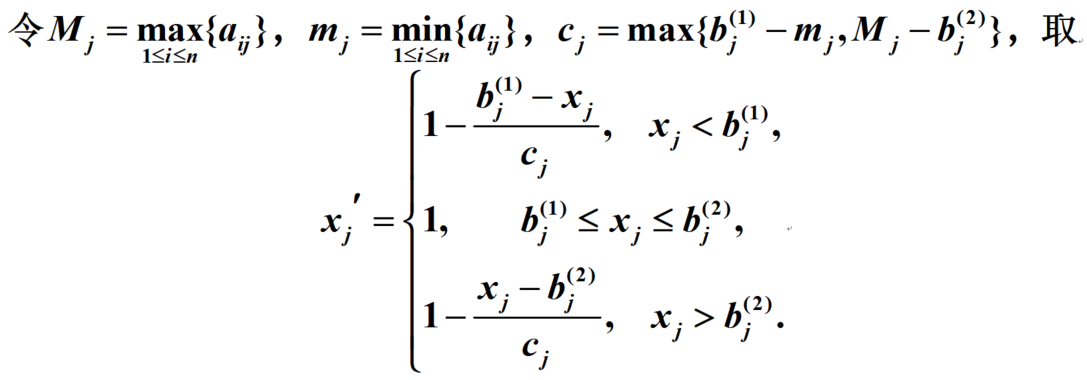
指标无量纲处理
将指标实际值转化为指标评价值
标准样本变换：

说明：这个变换处理会出现负值，将不能直接用于后续的熵权法/几何加权法

比例变换法：变换签后属性值成比例

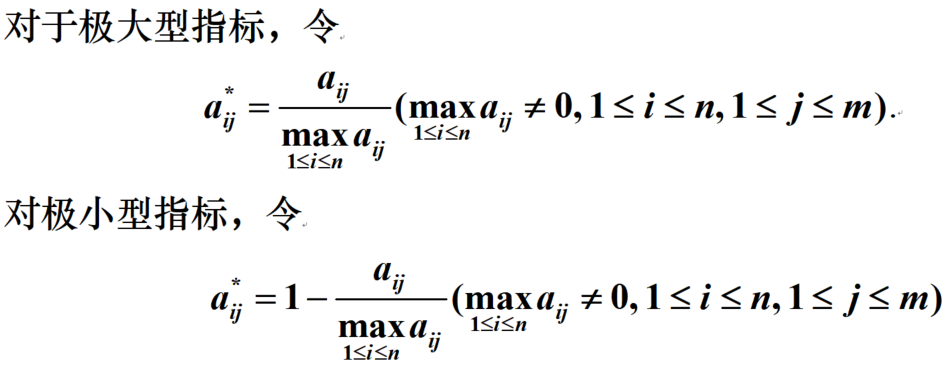
向量归一化法：

极差变换法：变换后$0\le a_{ij}^{?}\le 1$

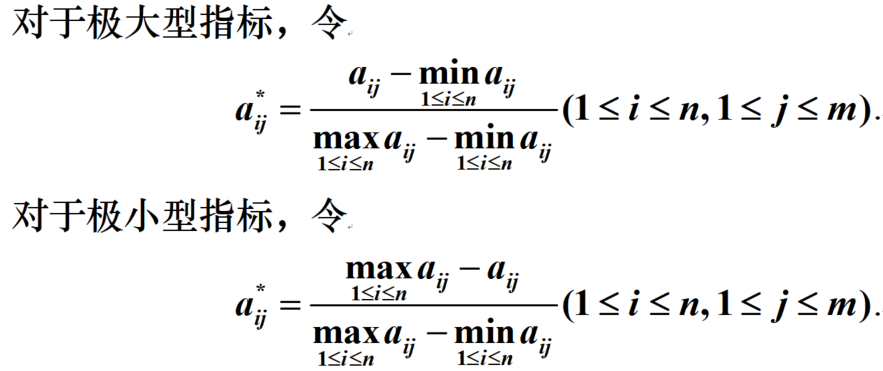
功效系数法：

定性指标定量化

评价指标预处理示例

根据下表所示的最大速度、飞行半径、最大负载、隐身性能、可靠性、灵敏度六个指标综合评价$A_1,A_2,A_3,A_4$四种战斗机性能

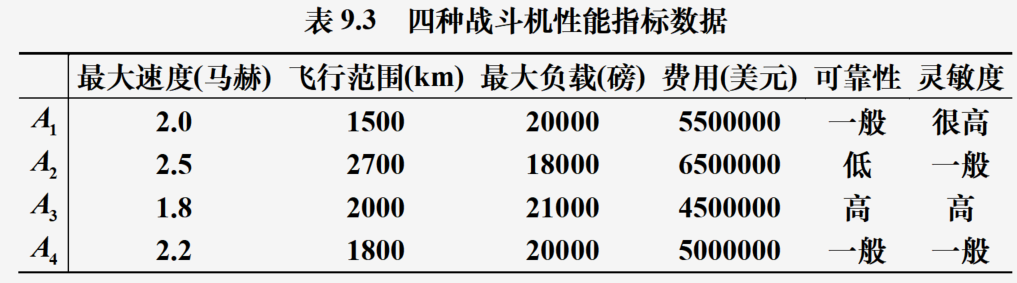
求解：
将6项指标依次记为$x_1,x_2,...,x_6$，将$x_5$和$x_6$两项定性指标定量化

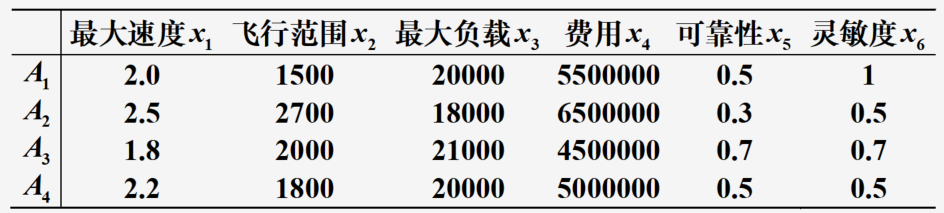
分别使用向量归一化、比例变换法和极差变换法标准化数值性指标数据

import numpy as np
import pandas as pd
a=np.loadtxt("Pdata9_1_1.txt",)
R1=a.copy(); R2=a.copy(); R3=a.copy()  #初始化
#注意R1=a,它们的内存地址一样，R1改变时，a也改变
for j in [0,1,2,4,5]:
    R1[:,j]=R1[:,j]/np.linalg.norm(R1[:,j]) #向量归一化
    R2[:,j]=R1[:,j]/max(R1[:,j])     #比例变换
    R3[:,j]=(R3[:,j]-min(R3[:,j]))/(max(R3[:,j])-min(R3[:,j]));
R1[:,3]=1-R1[:,3]/np.linalg.norm(R1[:,3])
R2[:,3]=min(R2[:,3])/R2[:,3]
R3[:,3]=(max(R3[:,3])-R3[:,3])/(max(R3[:,3])-min(R3[:,3]))
np.savetxt("Pdata9_1_2.txt", R1); #把数据写入文本文件，供下面使用
np.savetxt("Pdata9_1_3.txt", R2); np.savetxt("Pdata9_1_4.txt", R3)
DR1=pd.DataFrame(R1)  #生成DataFrame类型数据
DR2=pd.DataFrame(R2); DR3=pd.DataFrame(R3)
f=pd.ExcelWriter('Pdata9_1_5.xlsx')  #创建文件对象
DR1.to_excel(f,"sheet1")  #把DR1写入Excel文件1号表单中,方便做表
DR2.to_excel(f,"sheet2"); DR3.to_excel(f, "Sheet3"); f.save()

常用的综合评价数学模型

综合评价数学模型：将同一评价对象不同方面的多个指标值综合在一起，得到一个整体性评价指标值的一个数学表达式
记号说明
$n$个评价对象，$m$个评价指标$x_1,x_2,...,x_m$
第$i$个评价对象的指标指$a_i=[a_{i1},a_{i2},...,a_{im}]$
经过指标数据预处理得到的结果为$b_i=[b_{i1},b_{i2},...,b_{im}]$
指标变量的权重系数？？？怎么得到

线性加权综合评价模型

利用指标变量的权重系数$w=[w_1,w_2,...,w_m]$
$$f_i=\sum _{j=1}^m{w}_j{b}_{ij}(i=1,2,...,n)$$
说明：适合各个评价指标相互独立的情况，若各个评价指标不完全独立将导致各指标间信息的重复起作用

TOPSIS法

正理想解和负理想解构造

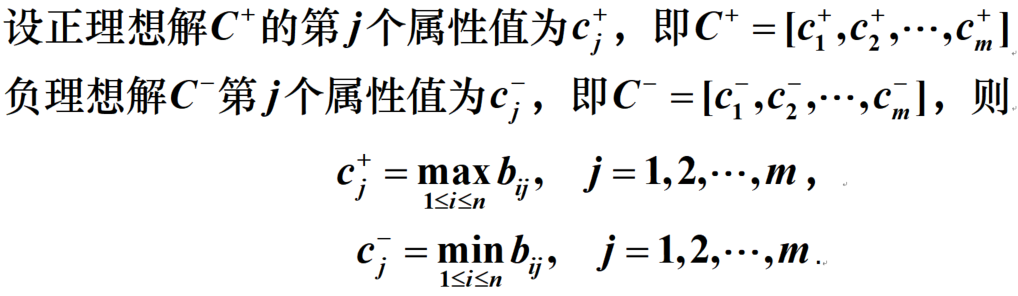
加权TOPSIS方法
根据得到的权重向量$w$，修改评价矩阵$B=(b_{ij}{)}_{nxm}$，得到加权规范评价矩阵$\hat{B}$，其中每个值$\widehat{b_{ij}}=w_j{b}_{ij}$，用$\hat{B}$按照上面的步骤进行处理

灰色关联度分析

设综合评价问题中有$n$个评价对象$m$个指标，相应的指标观测值分别为
$$a_{ij}(i=1,2,...,n;j=1,2,...,m)$$
具体步骤：
（1）数据预处理：对评价数据进行一致化和无量纲化处理，得到评价矩阵$B=(B_{ij}{)}_{nm}$
（2）确定比较序列和参考序列：比较序列即为矩阵$B$的每一行，参考序列相当于TOPSIS方法中的最优解，记作$b_0$

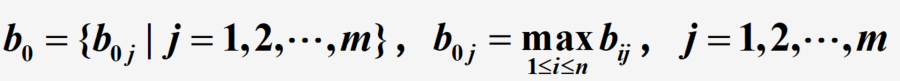
（3）计算灰色关联系数：

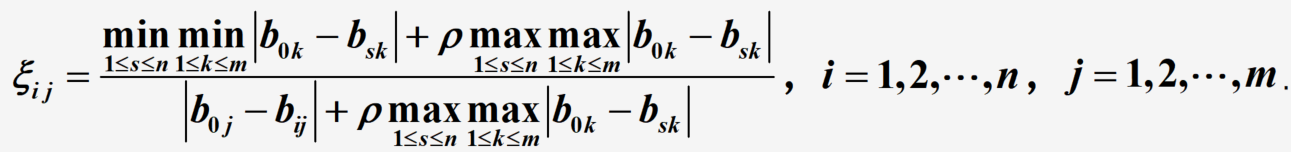
说明：上式计算的是比较序列$b_i$对参考序列$b_0$在第$j$个指标上的关联系数；$\sigma \in [0,1]$为分辨系数，分辨系数与分辨率正相关；称$mi{n}_{1\le s\le n}mi{n}_{1\le k\le m}|b_{0k}?b_{sk}|$为两级最小差，$ma{x}_{1\le s\le n}ma{x}_{1\le k\le m}|b_{0k}?b_{sk}|$为两级最大差
（4）计算灰色关联度：

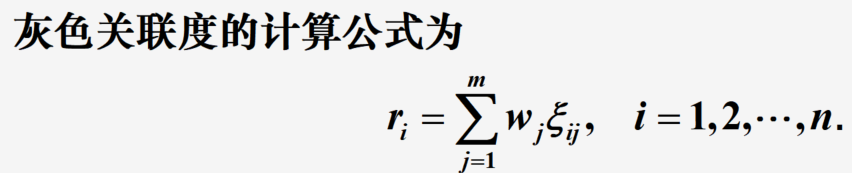
说明：式子中$w_j$为第$j$个指标的权重，计算结果$r_i$为第$i$个评价对象对理想对象的灰色关联度
（5）评价分析：
根据灰色关联度值对各评价对象进行排序，关联度越大评价结果越好

熵值法

使用目的：根据各指标的相对变化程度对系统整体的影响来确定指标权重系数

1. 计算第$i$个评价对象在第$j$项指标的特征比重$p_{ij}$
   
2. 计算第$j$项指标的熵值
   
3. 计算第$j$项指标的差异系数$g_i$
   
4. 确定第$j$项指标的权重系数
   
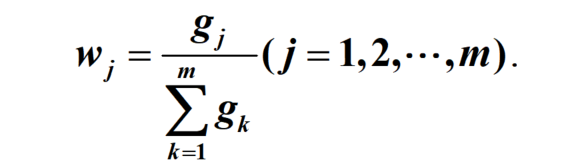
5. 计算第$i$个评价对象的综合评价值
   
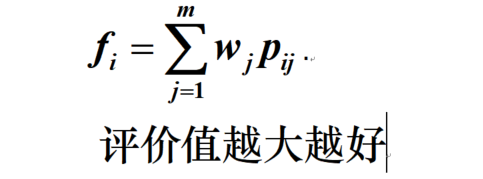
   说明：在计算综合评价值时，可以只是使用熵值法来计算各个指标的权重系数，利用求得的权重系数结合其他综合评价方法得到各个评价对象的综合评价直，比如熵权法+TOPSIS方法为常用的综合评价策略

秩和比（RSR）法

Rank Sum Ratio, RSR
基本原理
在$n$行$m$列矩阵中通过秩转化，获得无量纲统计量RSR，使用RSR值对评价对象直接排序
样本秩

举个例子说明样本数据的秩统计量

设综合评价问题中有$n$个评价对象$m$个指标，相应的指标观测值分别为
$$a_{ij}(i=1,2,...,n;j=1,2,...,m)$$
构造得到数据矩阵$A=(a_{ij}{)}_{nm}$
步骤
（1）编秩：对数据矩阵$A$逐列编秩，即分别编出每个指标值的秩。具体为：将极大型指标从小到大编秩，极小型指标从大到小编秩，指标值相同时编平均秩，得到秩矩阵$R=(R_{ij}{)}_{nm}$
（2）计算秩和比（RSR）：$RS{R}_i=\frac{1}{n}{\sum }_{j=1}^m{w}_j{R}_{ij}$，$w_j$为第$j$个指标的权重
（3）秩和比排序：RSR值越大，评价结果越好

综合评价示例

例题：

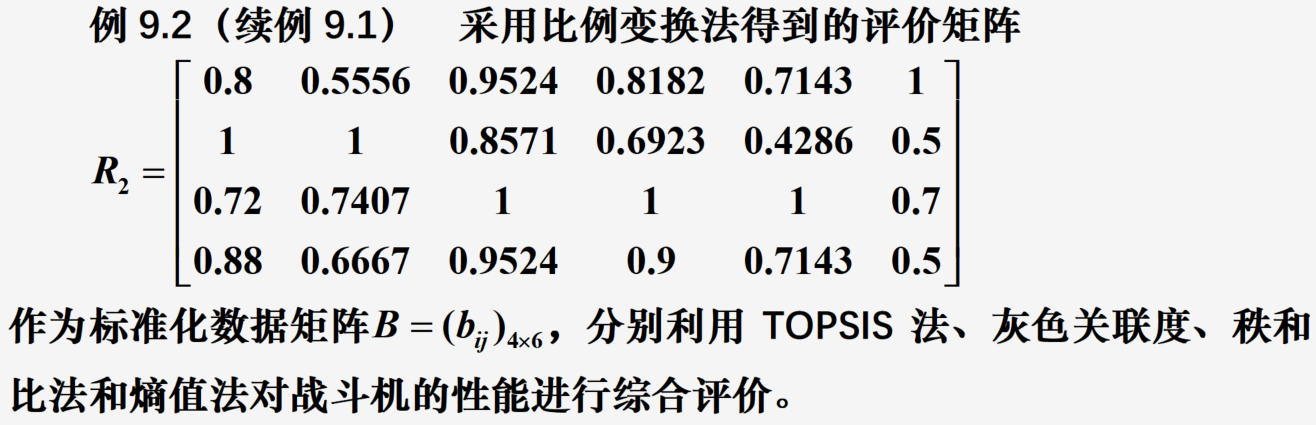
代码：

import numpy as np
from scipy.stats import rankdata
a=np.loadtxt("Pdata9_1_3.txt")
cplus=a.max(axis=0)   #逐列求最大值
cminus=a.min(axis=0)  #逐列求最小值
print("正理想解=",cplus,"负理想解=",cminus)
d1=np.linalg.norm(a-cplus, axis=1)  #求到正理想解的距离
d2=np.linalg.norm(a-cminus, axis=1) #求到负理想解的距离
print(d1, d2)   #显示到正理想解和负理想解的距离
f1=d2/(d1+d2); print("TOPSIS的评价值为：", f1)
t=cplus-a   #计算参考序列与每个序列的差
mmin=t.min(); mmax=t.max()  #计算最小差和最大差
rho=0.5  #分辨系数
xs=(mmin+rho*mmax)/(t+rho*mmax)  #计算灰色关联系数
f2=xs.mean(axis=1)  #求每一行的均值
print("\n关联系数=", xs,'\n关联度=',f2)  #显示灰色关联系数和灰色关联度
[n, m]=a.shape
cs=a.sum(axis=0)  #逐列求和
P=1/cs*a   #求特征比重矩阵
e=-(P*np.log(P)).sum(axis=0)/np.log(n)  #计算熵值
g=1-e   #计算差异系数
w = g / sum(g)  #计算权重
F = P @ w   #计算各对象的评价值
print("\nP={}\n,e={}\n,g={}\n,w={}\nF={}".format(P,e,g,w,F))
R=[rankdata(a[:,i]) for i in np.arange(6)]  #求每一列的秩
R=np.array(R).T   #构造秩矩阵
print("\n秩矩阵为：\n",R)
RSR=R.mean(axis=1)/n; print("RSR=", RSR)