LCA算法-Tarjan算法

前言

LCA（lowest common ancestor）问题，是初学基础数据结构——二叉树时的经典例题，对于单次求最近公共祖先我们可以在O(n)的时间复杂度内完成，但是对于多次求任意两点的最近公共祖先，显然就不是那么容易了，对于LCA问题，我们一般有两种解法——倍增算法和Tarjan算法，本文来介绍Tarjan算法求解LCA问题。

相信大多数算法学习者对于Robet Tarjan这个大佬都不会陌生，我们熟悉的强连通分量双连通分量问题的高效算法他都有建树，甚至还参与开发了斐波那契堆、伸展树 orz。

对于倍增法LCA见：LCA算法-倍增算法

---

Tarjan-LCA算法

Tarjan算法也是一种离线算法，它巧妙利用了并查集和回溯法实现了在O(n + m)内解决LCA问题（n为节点数目，m为查询次数）。

算法原理

我们已经知道了所有的查询，只是需要一种方法高效地处理出所有查询罢了，我们不妨设函数Tarjan(x)能够处理以x为根的子树内的所有查询。

那么对于子树x内的查询而言可以分为三种：

1. 查询的两个节点都在x的同一棵子树内，
2. 查询的两个节点在x的两个不同子树内，
3. 查询的两个节点一个是根x，一个在x的一棵子树内。

那么我们可以先解决子树内的查询1、2，再解决查询3

但是对于查询3我们无法直接根据查询信息获得，我们只能知道所有的query(x , i)（注意i不一定在子树x内）

比如如下情况：

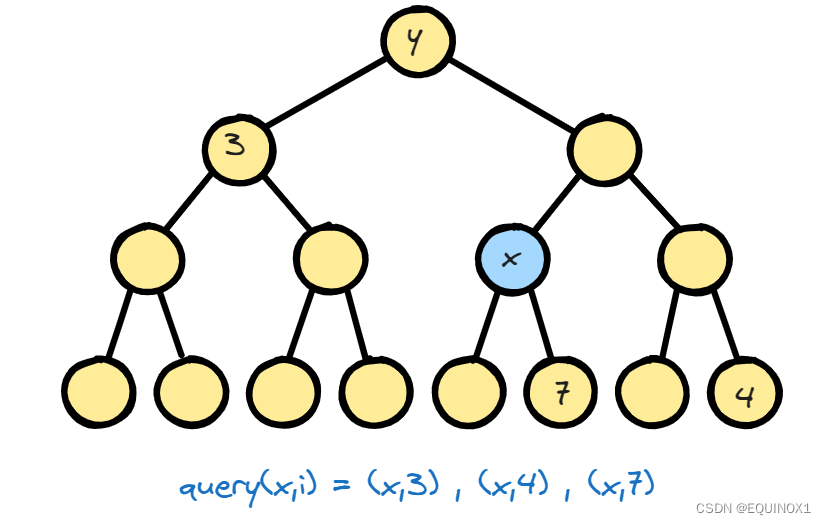
我们发现只有query(x,7)是符合3的，显然query(x,7) = x

那么query(x,3)和query(x,4)呢？

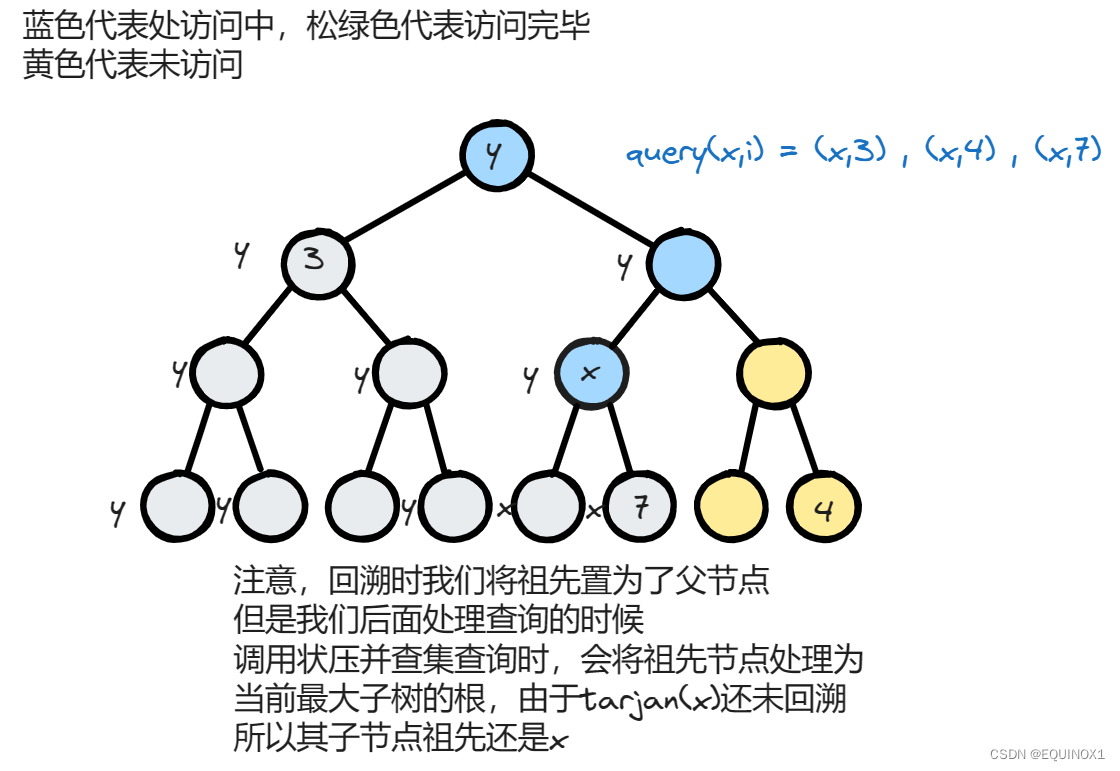
我们前面提过了，我们的tarjan(root)方法是先解决root所有子树的查询，再来处理查询3，也就是说当我们进行tarjan(x)，并且遍历所有的query(x,i)时，在上图中此时query(x,3)是已经解决了的，也就是说tarjan(x)是tarjan(y)的分支，在图中我们可以观察出query(x,3) = y，而且已知已经进行过tarjan(3)了，于是我们在tarjan(3)回溯的时候记录节点3的祖先为y并给3打上访问标记，那么我们在处理query(x,3)的时候就直接可以以3的祖先为query(x,3)的答案

因为如果对于query(x,i)，其中tarjan(i)已经进行过了，说明x，i此时都在tarjan(y)的递归分支中,y是它们的公共祖先，而由于我们回溯后对祖先进行了处理，所以此时i的祖先就是x和i的最近公共祖先。

可以结合图来理解

算法实现

• 预处理

  • query[x]存储了所有的query(x,i)，p[x]为并查集数组,，标记数组vis[i]，表示访问过节点i
  • 预处理存储所有的访问，
  • 初始化p[i] = i
  • 调用tarjan(root)

• tarjan(u)

  • vis[u] = 1
  • 访问u的相连节点v未访问过的就tarjan(v)，处理v子树内的询问，回溯时p[v] = u;
  • 遍历所有query[u]
  • 对于query(u,i)，如果i已经访问过，那么query(u,i) = findp(i)

代码详解

#define N 500050
typedef pair<int, int> PII;
vector<vector<int>> g(N);//存图
vector<PII> query[N];//存储查询
int p[N], ans[N];//并查集数组和查询结果数组
bitset<N> vis;//标记数组
int findp(int u)//状压查询
{
    return u == p[u] ? u : p[u] = findp(p[u]);
}
void tarjan(int u)
{
    vis[u] = 1;
    for (auto v : g[u])
    {
        if (!vis[v])
        {
            tarjan(v);
            p[v] = u;//回溯处理
        }
    }
    for (auto &q : query[u])
    {
        auto [v, i] = q;
        if (vis[v])
            ans[i] = findp(v);
    }
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    int n, m, s, a, b;
    cin >> n >> m >> s;
    for (int i = 1; i < n; i++)
    {
        cin >> a >> b;
        g[a].emplace_back(b);
        g[b].emplace_back(a);
    }
    for (int i = 1; i <= m; i++)
    {
        cin >> a >> b;
        if (a == b)//特殊情况直接给答案节省时间
            ans[i] = a;
        else
        {//查询预处理
            query[a].emplace_back(b, i);
            query[b].emplace_back(a, i);
        }
    }
    for (int i = 1; i <= n; i++)
        p[i] = i;
    tarjan(s);
    for (int i = 1; i <= m; i++)
        cout << ans[i] << '\n';
    return 0;
}

OJ链接

P3379 【模板】最近公共祖先（LCA） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

[P4211 LNOI2014] LCA - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)