【信号与系统】【北京航空航天大学】实验一、信号的MATLAB表示及信号运算

一、实验目的

1、初步掌握 MATLAB 仿真软件的使用；
2、学习使用 MATLAB 产生基本时域信号，并绘制信号波形；
3、学习利用 MATLAB 实现信号的基本运算；
4、利用 MATLAB 分析常用的连续时域信号。

二、实验内容

1、 生成连续信号

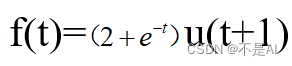
，并在自变量范围 （-2，4） 内绘图。

MATLAB代码：

>> clear all;
>> t = -2:0.01:4;
>> f = (2 + exp(-t)) .* (t >= -1) + 0 * (t < -1);
>> plot(t, f)
>> axis([-2 4 -0.5 5])

生成的信号波形图：

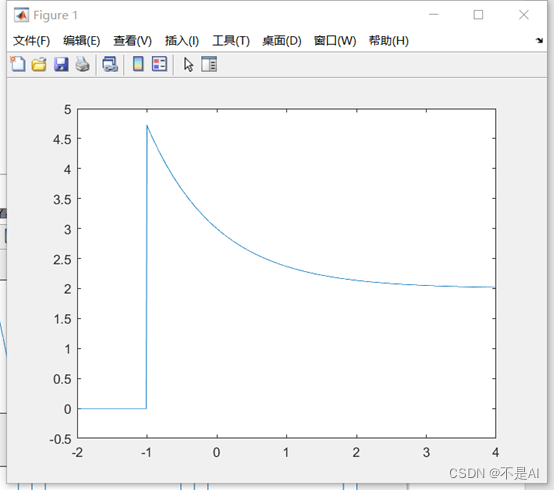
2、 生成连续信号

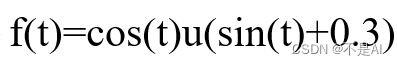
，并在自变量范围 （-10，10） 内绘图。

MATLAB代码：

>> clear all;
>> t = -10:0.01:10;
>> f = cos(t) .* ((sin(t) + 0.3) >= 0) + 0 * ((sin(t) + 0.3) < 0);
>> plot(t, f)
>> grid on

生成的信号波形图：

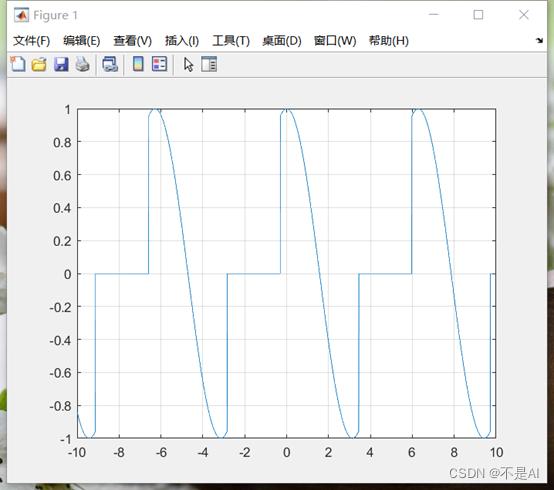
3、 生成离散信号

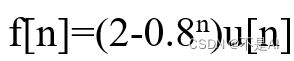
，并在自变量范围 （-2，4） 内绘图。

MATLAB代码：

>> clear all;
>> n = -2: 4;
>> f = (2 - 0.8.^n) .* (n >= 0) + 0 * (n < 0);
>> stem(n, f);

生成的信号波形图：

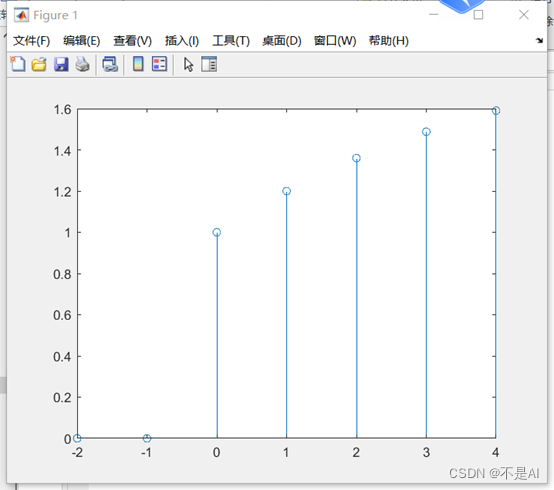
4、 在同一 figure 上绘制以下信号（提示，使用 subplot 函数）：

（1）

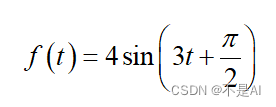
自变量范围 （-5,5）；

（2） 正弦序列

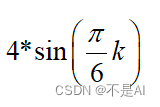
自变量范围 （-15,15）。

MATLAB代码：

>> clear all;
>> figure
>> subplot(2, 1, 1)
>> t = -5:0.01:5;
>> f = 4 * sin(3 * t + pi / 2);
>> plot(t, f)
>> subplot(2, 1, 2)
>> k = -15: 15;
>> f = 4 * sin(k * pi / 6);
>> stem(k, f)

生成的信号波形图：

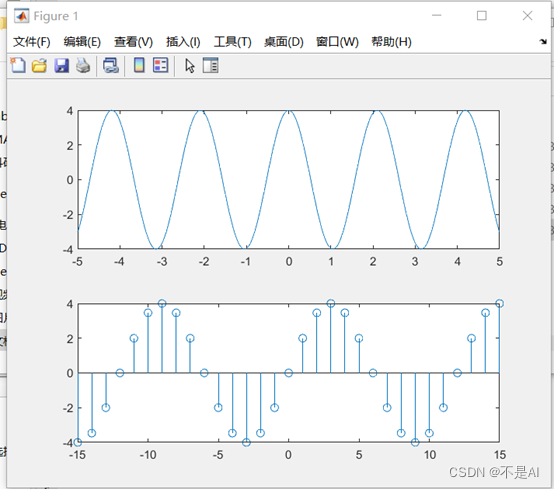
5、 在同一 figure 上绘制以下信号（提示，使用 subplot 函数）：

（1） 近似的冲激信号

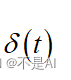
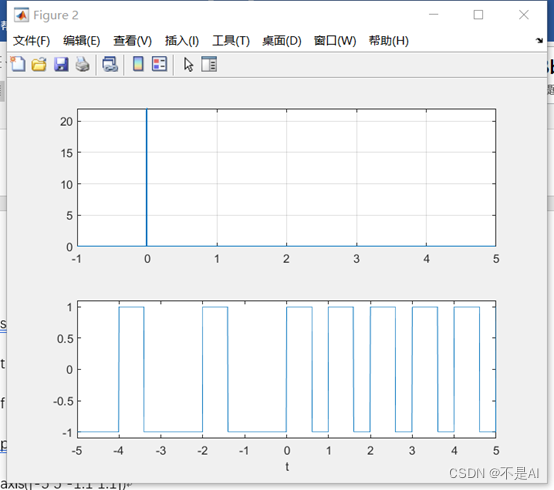
（2） 方波信号，要求 x < 0 时幅度为 ±1 ，周期为 2，占空比为 30%； x >= 0 时周期为 1，占空比为 60%。自变量取值范围为 （-5,5）。提示：可采用 u(t) 函数辅助做出该信号。

MATLAB代码：

>> clear all;
>> figure
>> subplot(2, 1, 1)
>> t0 = -1;
>> tf = 5;
>> dt = 0.01;
>> t1 = 0;
>> t = [t0 : dt : tf];
>> st = length(t);
>> n1 = floor((t1 - t0) / dt);
>> x1 = zeros(1, st);
>> x1(n1) = 1 / dt;
>> stairs(t, x1);
>> grid on;
>> axis([-1 5 0 22])
>> subplot(2, 1, 2);
>> t = -5 : 0.01 : 5;
>> f = square(pi * t, 30) .* (t < 0) + square(2 * pi * t, 60) .* (t >= 0);
>> plot(t, f);
>> axis([-5 5 -1.1 1.1]);
>> xlabel('t');

生成的信号波形图：

6、 已知信号 f1(t) 和 f2(t) 分别为：

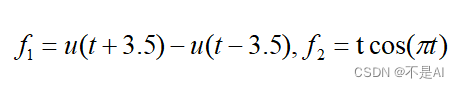
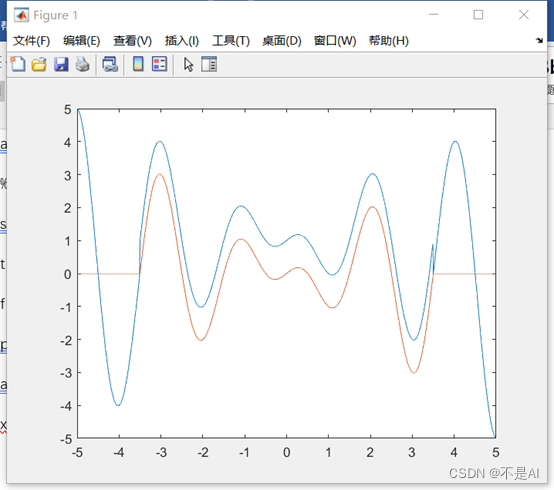
（1） 在同一张图上分别绘制 f1(t) + f2(t) 和 **f1(t) * f2(t) **的波形（使用 hold on 命令）；

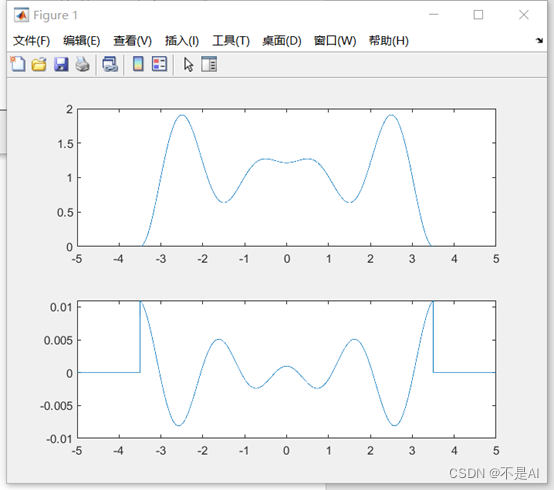
（2） 在同一张 figure 上分别绘制 f1(t) * f2(t) 的积分与微分结果（使用 subplot 命令）。

（1） MATLAB代码：

>> clear all;
>> %波形
>> t = -5: 0.01: 5;
>> f = 0 * (t >= 3.5) + 1 * (t >= -3.5 & t < 3.5) + 0 * (t < -3.5) + t .* cos(pi * t);
>> plot(t, f)
>> hold on;
>> g = t .* cos(pi * t) .* (t >= -3.5 & t < 3.5);
>> plot(t, g)

生成的信号波形图：

（2） MATLAB代码：

>> clear all;
>> figure
>> subplot(2,1,1)
>> dt = 0.001;
>> t = -5 : dt : 5;
>> mianji = 0;
>> f = t .* cos(pi * t) .* (t >= -3.5 & t < 3.5);
>> for i = 1 : 10001
mianji = mianji + f(i) * dt;
f2(i) = mianji;
end;
>> plot(t, f2);
>> f1 = diff(f);
>> subplot(2, 1, 2);
>> plot(t(1:10000), f1);

生成的信号波形图：

7、 已知信号

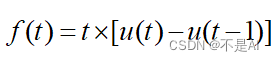
，在同一 figure 上绘制 f (t - 1), f (t + 2), f (0.5t), f (2t)（使用 subplot 命令）

MATLAB代码：

>> clear all;
>> figure
>> subplot(4, 1, 1);
>> t = -2: 0.01: 2;
>> f1 = (t - 1) .* ((t - 1) >= 0 & (t - 1) < 1);
>> plot(t, f1);
>> axis([0.5 2.5 0 1])
>> grid on;
>> subplot(4, 1, 2);
>> f2 = (t + 2) .* ((t + 2) >= 0 & (t + 2) < 1);
>> plot(t, f2);
>> axis([-2.5 -0.5 0 1])
>> grid on;
>> subplot(4, 1, 3);
>> f3 = (0.5 * t) .* (0.5 * t >= 0 & 0.5 * t < 1);
>> plot(t, f3)
>> axis([-0.5, 2.5 0 1])
>> grid on
>> subplot(4, 1, 4)
>> f4 = (2 * t) .* (2 * t >= 0 & 2 * t < 1);
>> plot(t, f4)
>> axis([-0.5, 1, 0, 1])
>> grid on

生成的信号波形图：

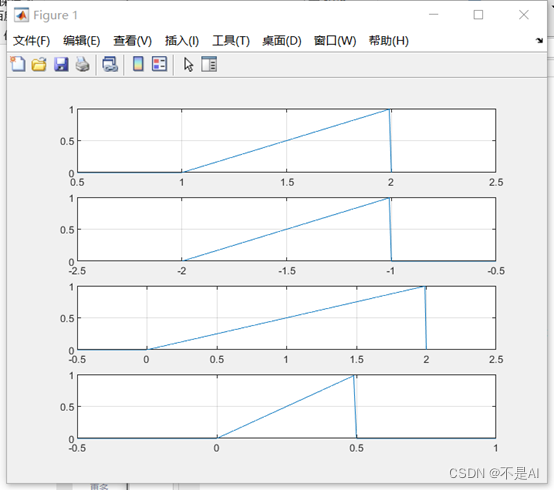
至此，本次实验结束。