搜索与图论第七期 Prime算法

前言

prime算法也是一种图的结构 ，哎图的结构还有好多好多，大家慢慢学吧！！！

一、prime 算法的基本内容

过程：

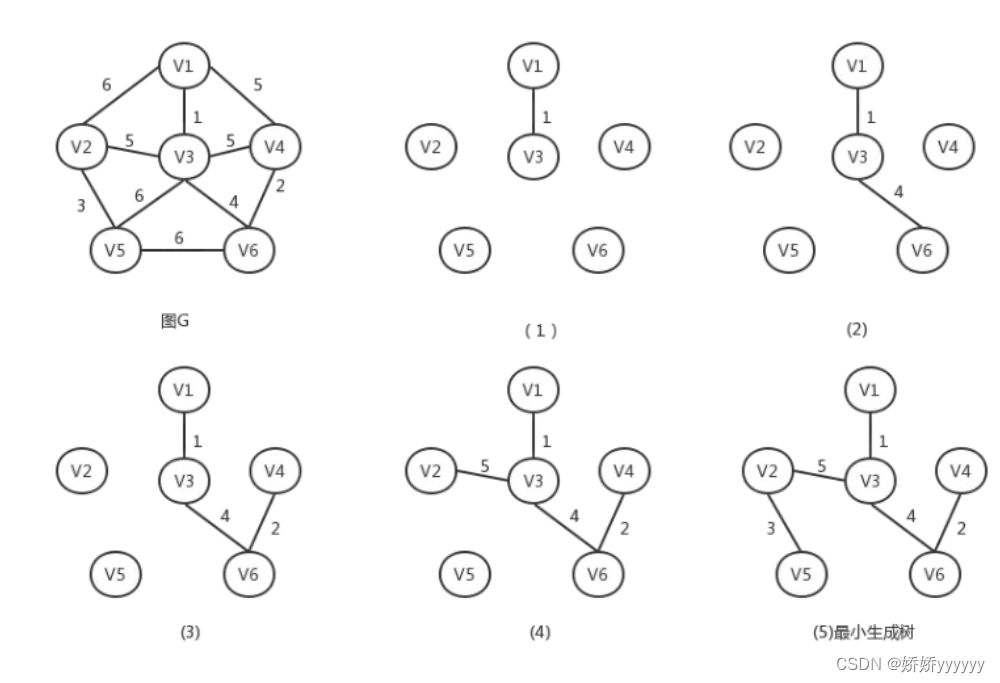
最小生成树prim算法简单理解他的寻找路径的过程，从一个顶点V0开始，首先找到所有与V0相关联的顶点，查看这些顶点到V0的加权值，找出最小的一个，然后将该顶点纳入已统计顶点中。

寻找第三个顶点时，将V0、之前已算出的顶点与所有相关联且未统计的顶点，找出最小的一个，纳入已统计顶点中。

prim算法

是实现图的最小生成树。既然是图，就假设包含n个顶点，m条边。prim算法是从顶点出发的，其算法时间复杂度与顶点数目有关系。

从某个顶点开始，假设v0，此时v0属于最小生成树节点中的一个元素，该集合假设u，剩下的V-v0为待判定的点，此时选取u中的顶点到V-v0中顶点的一个路径最小的边，并且将其中非u中的顶点加入到u中，循环直到u中的顶点包含图所有的顶点为止。

最小生成树prim的优缺点：

优点：当边多且有重复边时，kruskal算法会超时。但是可以用prim算法去边，所以点多的时候用kruskal算法，边多的时候用prim算法，就可以去边了。缺点：使用kruskal算法会再有重复边的时候超时。

图示：

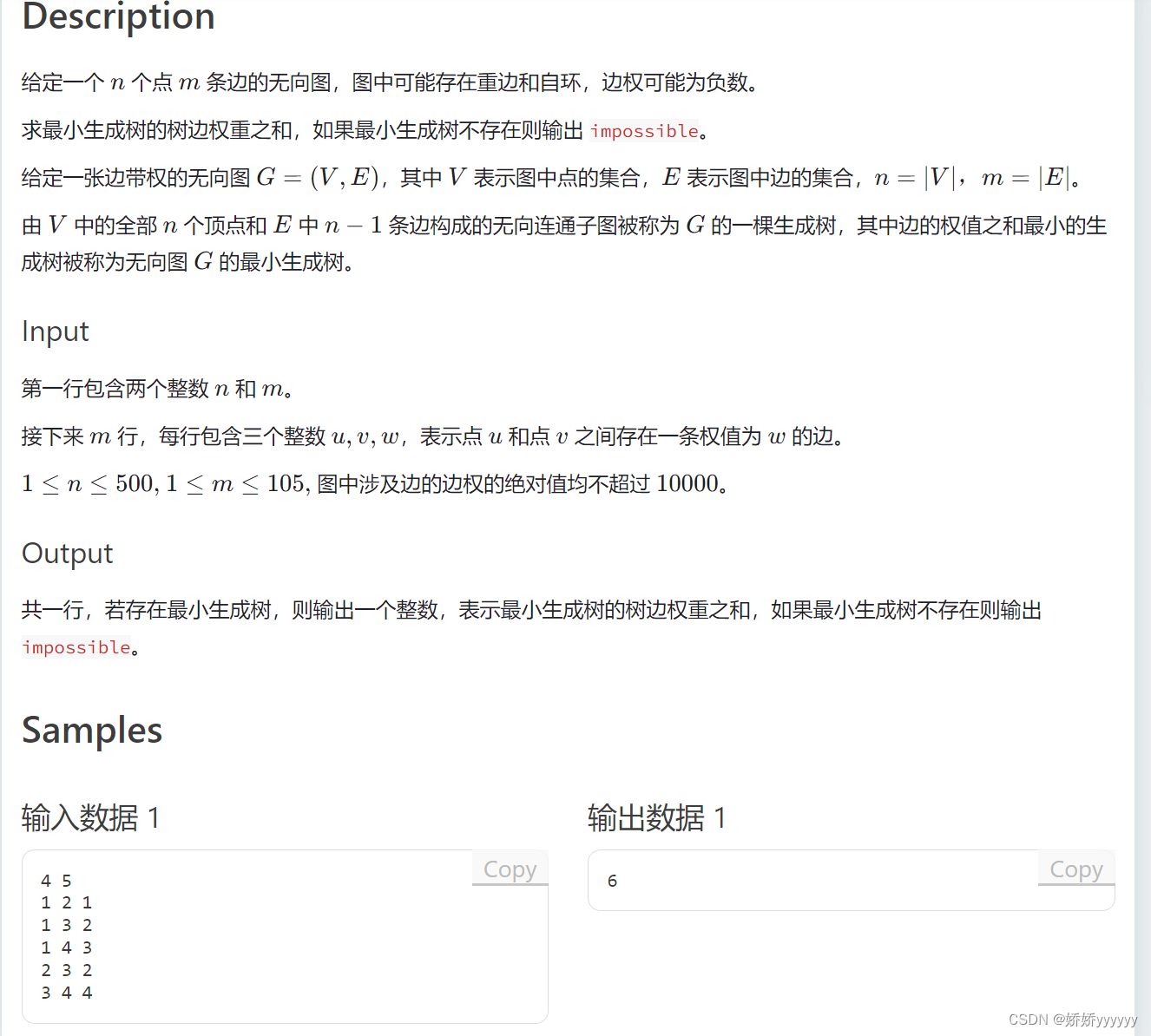
二、例题

1：Prime算法求最小生成树

2.AC代码：

#include <bits/stdc++.h>

using namespace std;

const int N = 510, M = 100010, INF = 0x3f3f3f3f;

int n, m;
int g[N][N], dist[N];
bool st[N];

int prim()
{
    memset(dist, INF, sizeof dist);
    dist[1] = 0;
    int res = 0;
    for(int i = 0; i < n; i++)
    {
        int t = -1;
        for(int j = 1; j <= n; j++)
            if(!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;

        if(dist[t] == INF)
            return INF;
        
        st[t] = true;
        res += dist[t];
        for(int j = 1; j <= n; j++)
            dist[j] = min(dist[j], g[t][j]);
    }
    return res;
}

int main()
{    
    cin >> n >> m;
    memset(g, INF, sizeof g);

    while(m--)
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b], c);
    }
    
    int res = prim();
    if(res == INF)    
        cout << "impossible" << endl;
    else
        cout << res << endl;

    return 0;
}

总结

总结来说图的内容很多很多，一步一步学吧，感谢大家的观看！！！