「达摩院MindOpt」优化形状切割问题（MILP）

1. 形状切割问题

在制造业，高效地利用材料不仅是节约成本的重要环节，也是可持续发展的关键因素。无论是在金属加工、家具制造还是纺织品生产中，原材料的有效利用都直接影响了整体效率和环境影响。

形状切割问题（Shape Cutting or Cutting Stock Problem），以其多变的问题形式和实际应用的广泛性，成为了运筹学和优化领域中一个非常有趣且具有挑战性的研究课题。简单来说，这个问题要求我们从一块给定尺寸的材料中切割出一系列预定形状的物品，目的是最大化材料的使用效率，同时最小化浪费。虽然表述看似直白，但实际解决过程却充满了复杂性。

一维切割、二维切割、三维切割，对应的需要考虑的约束会指数升级，对应的解决方案可能会不一致。比如一维控制量只有长度，二维就有坐标x,y和转角，三维就对应x,y,z，和Roll, Pitch, Yaw三种选择角度。切割的形状不能重叠的表达也会变得非常的复杂。

本文先仅探讨一维切割问题。

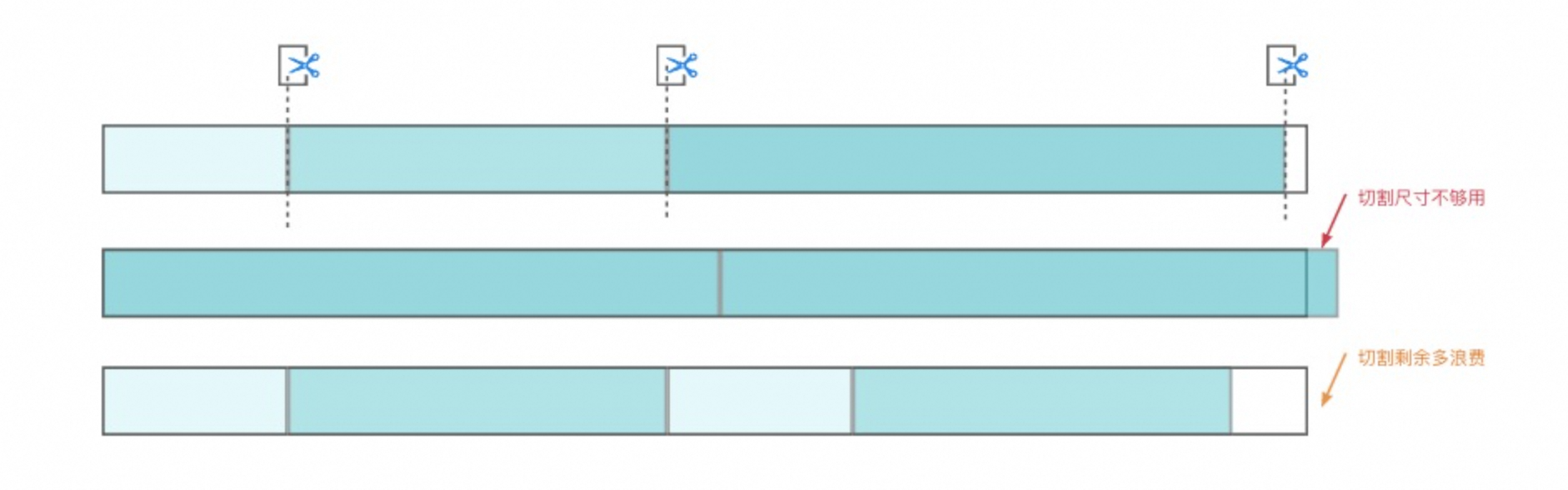
一维切割的思路，扩展一下，在实际中也有很多应用，如：

• 钢筋切割，将统一的长钢筋原材料，根据需求切割成不同长度小尺寸，如何切割能最小化使用的原材料数。
• 木材加工，从长度不一的原材料木材中，切割出多种长度的小段，如何切割能最大化成品总长度数，提高原木材利用率。
• 计算资源分配，将不同规格的机器，容器化成多个虚拟计算资源，如何划分能满足用户的使用需求，提高在使用机器的利用率。
• 时间管理，将完整的工作日或项目周期分配给多个任务，使得每个任务都有足够的时间完成，同任务尽量连续时间，避免频繁切换导致时间浪费。
• 货运装箱，在物流运输中，如何将一堆不同大小的货物合理地分配给不同的货车或者集装箱，有效提高装载效率，降低货运成本。此问题在有些场景可以用一维问题来表示，还有很多厂家是需要3维装箱问题来表达。

2. 一个具体的问题示例

假设我们有一批长度统一为100单位的水管原材料，需要切割出不同的长度，需求为

• 14单位长度的小段 5个
• 50单位长度的小段 7个
• 70单位长度的小段 3个
  请问，如何安排切割，使用的原材料数目最少？

3. 数学建模和数据整理

这个问题我们用数学规划的方式建模如下：

汇总的数学模型为：

---

min ? f u s e d s.t. f u s e d = ∑ i ∈ R b i ∑ i ∈ R x i , j ≥ d j , N u m , ? j ∈ D ∑ j ∈ D x i , j ? d j , S i z e ≤ L ? b i , ? i ∈ R b i ∈ { 0 , 1 } , ? i ∈ R x i , j 是整数 , ? k , i ∈ I \begin{array}{rll} \min & f_{used} & \\ \text{s.t.} & f_{used} = \sum_{i \in R}b_{i} &\\ & \sum_{i \in R} x_{i,j} \geq d_{j,Num}, & \forall j \in D \\ & \sum_{j \in D} x_{i,j} \cdot d_{j,Size} \leq L \cdot b_{i}, & \forall i \in R \\ & b_{i} \in \{0,1\}, & \forall i \in R\\ & x_{i,j} 是整数, & \forall k,i \in I \end{array} mins.t.?fused?fused?=∑i∈R?bi?∑i∈R?xi,j?≥dj,Num?,∑j∈D?xi,j??dj,Size?≤L?bi?,bi?∈{0,1},xi,j?是整数,??j∈D?i∈R?i∈R?k,i∈I?

---

4. MindOpt APL 建模和求解

MindOpt APL 简称（MAPL），是一款代数建模语言。更适合数学优化模型开发者的语言。建模更高效，可调用多款优化求解器。

代码解析

决策变量

1. 变量x_pipeUsed，表示在满足所有需求后总共被使用的管道（水管原材料）数量。这是一个连续变量，但实际应用中通常会被当作整数处理，因为你不能使用部分水管。
2. 变量var x_cuts[rawPipe] >= 0 binary; 定义了一个索引为 rawPipe（原材料水管编号集合）的二元变量数组 x_cuts。每个元素 x_cuts[i] 表示编号为 i 的原材料水管是否被切割使用：1 表示被切割使用，0 表示未被使用。由于这是一个二元变量，所以其值被限定为 0 或 1。
3. 变量var x_cutNum[rawPipe,Demand] >= 0 integer; 定义了一个整数变量数组 x_cutNum，其索引为 rawPipe（原材料水管编号集合）和 Demand（需求序号集合）的笛卡尔积。每个元素 x_cutNum[i,j] 表示在编号为 i 的原材料水管中，编号为 j 的需求长度被切割出来的数量。整数变量意味着这些变量的值必须为非负整数。

决策目标

minimize Totalpipes: x_pipeUsed;

最小化变量 x_pipeUsed 的值，即最小化总共被使用的管道数。

约束

1. constraint_0 (管道使用总数约束): 这个约束确保变量 x_pipeUsed（被使用的管道总数）等于所有被切割的原材料管道数量的合计。换句话说，每个被切割使用的原材料管道都被计算在内。

subto constraint_0:
     sum {i in rawPipe} x_cuts[i] == x_pipeUsed;

这里，x_cuts[i] 是一个二元变量，表示原材料管道 i 是否被切割使用。如果被切割使用，则 x_cuts[i] 为 1，否则为 0。所有这些值加起来应该等于 x_pipeUsed。

---

2. constraint_1_DemandFulfillment (需求满足约束): 这个约束确保每个需求的数量 demandNum[j]（需求 j 的数量）都不超过通过切割原材料管道得到的对应尺寸的数量。

subto constraint_1_DemandFulfillment:
    forall { j in Demand}
        demandNum[j] <= sum{i in rawPipe} x_cutNum[i,j];

这里，x_cutNum[i,j] 表示从原材料管道 i 切割出的满足需求 j 的数量。所有原材料管道对该需求的贡献加起来，应该至少等于需求的数量。

---

3. constraint_1_CuttingLimit (切割限制约束): 这个约束确保每个被使用的原材料管道 i 切割出的产品总长度不超过该原材料管道的实际长度。

subto constraint_1_CuttingLimit:
    forall { i in rawPipe}
        sum{j in Demand} x_cutNum[i,j] * demandSize[j] <= pipe_length * x_cuts[i];

这里，demandSize[j] 是需求 j 的尺寸，pipe_length 是原材料管道的长度，x_cutNum[i,j] 是从原材料管道 i 切割出的满足需求 j 的数量。对所有的需求尺寸的切割长度求和，得到的总长度不应超过原材料管道的长度乘以该管道是否被使用的标志（如果管道未被使用，x_cuts[i] 为 0，因此等式右侧为 0，满足约束）。

---

完整源代码

完整代码如下：

clear model;
option modelname cutting_01; #定义存储文件名

# ----------建模--------Start----
# cutting_01.mapl

# 标准水管长度
param pipe_length = 100; 

# 需要切割的小段尺寸和对应的数量

param fileDir = "data/";
set Demand = {read fileDir+"Demand.csv" as "<1n>" skip 1}; # 读取需求序号
param demandSize[Demand] = read fileDir+"Demand.csv" as "<1n> 2n" skip 1; # 读取需求长度
param demandNum[Demand]  = read fileDir+"Demand.csv" as "<1n> 3n" skip 1; # 读取需求个数


# 假设总共有15根原材料
param pipe_Num = 15;
set rawPipe = {1..pipe_Num};

## 决策变量：
var x_pipeUsed; #总共被使用的管道数

# 各个原材料是否被切割
var x_cuts[rawPipe] >= 0 binary; 

# 每个原材料中，各种demandSize的需求被切割生产出来的数量
var x_cutNum[rawPipe,Demand] >= 0 integer; 


# 目标函数：最小化使用的水管原材料数量
minimize Totalpipes: x_pipeUsed;


## 约束条件：
# pipes_used 等于被切割原材料的求和。
subto constraint_0:
     sum {i in rawPipe} x_cuts[i] == x_pipeUsed;

# 切割后，各个尺寸的需求得到满足
subto constraint_1_DemandFulfillment:
    forall { j in Demand}
        demandNum[j] <= sum{i in rawPipe} x_cutNum[i,j];
        
# 每个原材料的切割方式，不超过总长度*被使用
subto constraint_1_CuttingLimit:
    forall { i in rawPipe}
        sum{j in Demand} x_cutNum[i,j] * demandSize[j] <= pipe_length * x_cuts[i] ;
        

#求解
option solver mindopt;     # （可选）指定求解用的求解器，默认是MindOpt
#option mindopt_options 'max_time=600'; #设置求解器参数
option mindopt_options 'print=0'; #设置求解器输出级别，减少过程打印
solve;         # 求解

# 结果打印和检查结果
print "----------------结果打印和存文件--------------";
#display; 
print "最小原材料耗费数 = ",x_pipeUsed;
print "原材料长度,需求1长度,需求1切割数,需求2长度,需求2切割数,需求3长度,需求3切割数,……";
forall { i in rawPipe with x_cuts[i] >= 0.5}
    print "{},|{},{},|{},{},|{},{},……"
        %pipe_length,demandSize[1],x_cutNum[i,1] ,demandSize[2],x_cutNum[i,2] ,demandSize[3],x_cutNum[i,3];


print "原材料长度,需求1长度,需求1切割数,需求2长度,需求2切割数,需求3长度,需求3切割数,……"
    : "切割方案.csv";
close "切割方案.csv";

forall { i in rawPipe with x_cuts[i] >= 0.5}
    print "{},{},{},{},{},{},{},……"
        %pipe_length,demandSize[1],x_cutNum[i,1] ,demandSize[2],x_cutNum[i,2] ,demandSize[3],x_cutNum[i,3] >> "切割方案.csv";
close "切割方案.csv";

运行上述代码结果如下：

Running mindoptampl
wantsol=1
print=0
MindOpt Version 1.0.1 (Build date: 20231114)
Copyright (c) 2020-2023 Alibaba Cloud.

Start license validation (current time : 29-DEC-2023 17:46:36).
License validation terminated. Time : 0.007s


OPTIMAL; objective 7.00

Completed.
----------------结果打印和存文件--------------
最小原材料耗费数 = 7
原材料长度,需求1长度,需求1切割数,需求2长度,需求2切割数,需求3长度,需求3切割数,……
100,|14,2,|50,0,|70,1,……
100,|14,1,|50,0,|70,1,……
100,|14,2,|50,0,|70,1,……
100,|14,0,|50,2,|70,0,……
100,|14,0,|50,2,|70,0,……
100,|14,0,|50,1,|70,0,……
100,|14,0,|50,2,|70,0,……