统计学R语言实验7 方差分析

统计学R语言实验7??方差分析

一、实验目的

1. 掌握理解方差分析的相关概念。

2. 掌握理解方差分析的相关方法。

3. 熟悉R语言等语言的集成开发环境。

二、实验分析与内容

完成教材P117的第4题

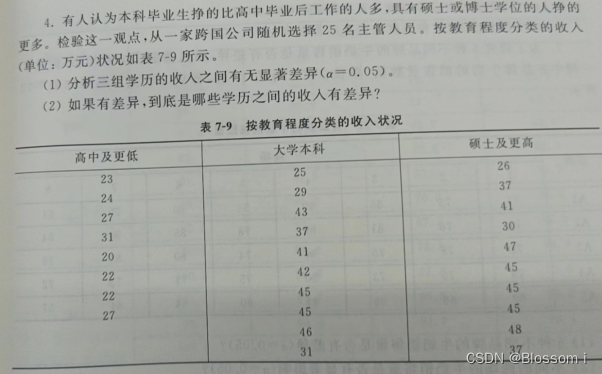
本题采用单因素方差分析来解题：

（1）分析三组学历的收入之间有无显著差异（a=0.05）

根据题目所给的数据，检验学历因素对工资收入是否有显著影响

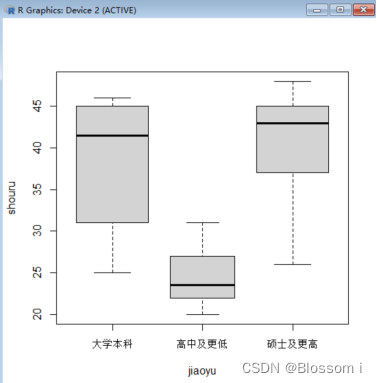
通过观察箱线图可以看出三种不同学历的公司员工的工资收入有明显的差异，所以猜测不同学历的工资收入也许有本质的差异。所以进行以下假设:

H0：u1=u2=u3 ?H1:u1,u2,u3不全相等

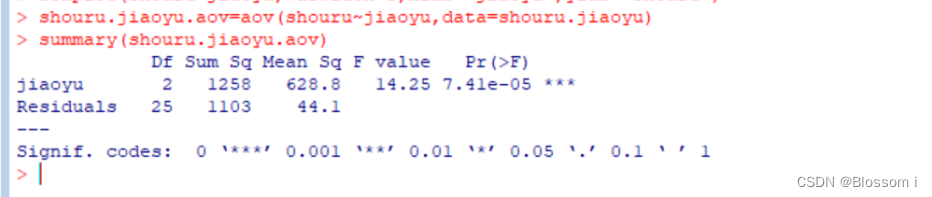
从方差分析结果来看，P值为7.41e-05，F值为14.25，F值大于临界值，P值大于0.05。所以有充分的证据拒绝H0，接受H1认为不同学历的成绩不相等。

（2）如果有差异，到底是哪些学历之间的收入有差异？

找出差异，通过summary提取相关信息：

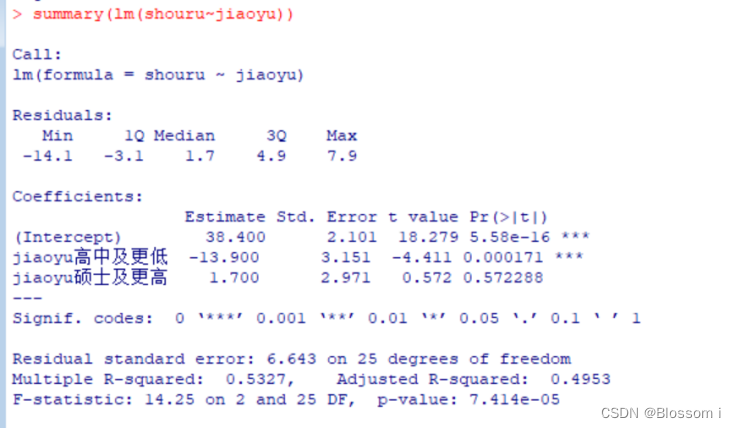
该命令得到一个类似回归分析的结果,包括回归系数以及它们的标准误差和t检验统计量。但是,这些系数的意义并不是通常的回归线斜率,而应该这样理解:截距这一项是大学本科工资收入的均值,而另外两个是相应组均值与大学本科工资收入这一组均值的差异。①

在上面的t检验部分里，可以发现大学本科工资收入与高中及更低的工资收入存在显著差异(p=0.000171),而大学本科工资收入与硕士及更高没有存在显著的差异(p=0.572288)。

通过采用Bonferroni修正方法，采用pairwise.t.test来计算所有的两组比较，并针对多重检验做出调整。

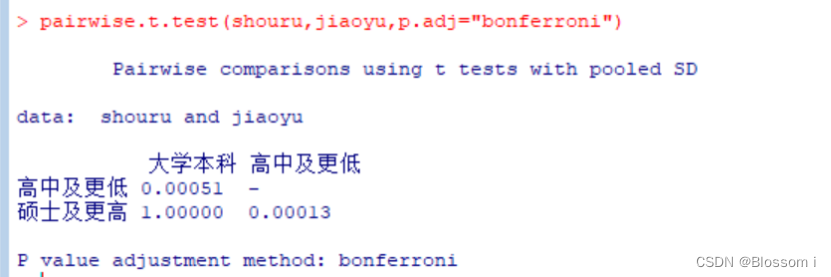
可以用Bartlett检验来看看某个变量的分布是否在所有组中都有一样的方差

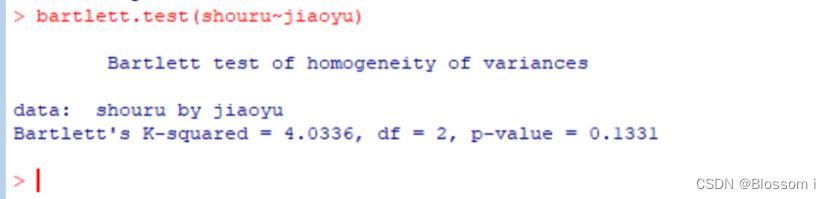
放宽对方差的假设

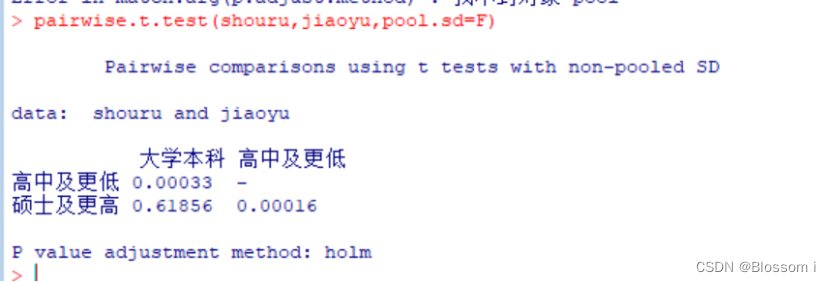
三、实验总结

单因素方差分析是一种用于比较两个或多个组之间均值差异的统计方法。在 R 语言中，可以使用 oneway.test 函数或 aov 函数进行单因素方差分析。oneway.test 函数可以计算不同组之间的均值和标准差，并检验它们是否显著不同。这个函数适用于数据分布偏斜较大的情况。函数语法：oneway.test(formula, data)

其中，formula 表示公式，用来指定要分析的数据列和分组变量；data 表示数据集。

aov 函数可以进行单因素方差分析，并提供了更多可选项，例如呈现多元分析数据和非常规数据的能力。该函数比 oneway.test 函数更灵活和通用性更强。

函数语法：aov(formula, data)其中，formula 和 data 的含义与 oneway.test 函数中相同。