多项式回归
多项式回归
- 多项式回归 是非线性回归的一种,之前讨论的线性回归都是直线,而多项式回归则是曲线的回归,它通过引入原始预测变量的高阶项(如平方、立方等)来拟合数据的非线性模式。
- 在多项式回归中,虽然模型对数据的关系是非线性的,但它依然是线性的,因为这种非线性体现在特征变换上,而不是模型的系数和变量之间的关系。这就是为什么多项式回归被视为线性回归的一个特例。
- 例如,一个二次多项式回归模型可以表述为 y = β 0 + β 1 x + β 2 x 2 + ? y = \beta_0 + \beta_1x + \beta_2x^2 + \epsilon y=β0?+β1?x+β2?x2+?,其中模型对于系数 (\beta) 是线性的,尽管它对于 (x) 是非线性的。
本文基于教程链接数据基于https://github.com/trekhleb/homemade-machine-learning/blob/master/data/non-linear-regression-x-y.csv
首先,我们取到的数据集散点图如下,这种情况下用一条直线来回归则有些不恰当:
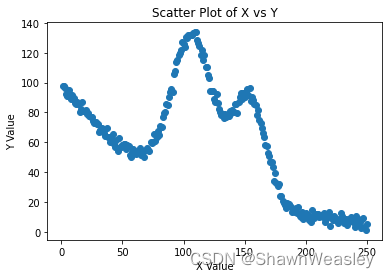
所以就需要使用一条多项式来模拟曲线回归。在多项式回归中最重要的就是选择多项式的复杂度,
Y
=
β
0
+
β
1
X
+
β
2
X
2
+
β
3
X
3
+
.
.
.
+
β
n
X
n
+
?
Y = \beta_0 + \beta_1X + \beta_2X^2 + \beta_3X^3 + ... + \beta_nX^n + \epsilon
Y=β0?+β1?X+β2?X2+β3?X3+...+βn?Xn+?多项式的复杂度(即公式中的n)不宜太低(欠拟合)或过高(过拟合)。如下图就是过低导致的欠拟合:
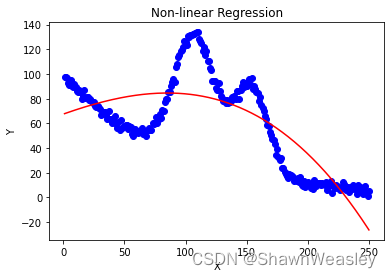
具体python代码如下:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split #用于划分训练集和测试集。
from sklearn.preprocessing import PolynomialFeatures #用于生成多项式特征。
from sklearn.linear_model import LinearRegression #用于执行线性回归。
from sklearn.metrics import mean_squared_error #用于评估模型性能。
# 导入数据
path = 'non-linear-regression-x-y.csv'
data = pd.read_csv(path)
# 分离特征和目标变量
X = data['x'].values.reshape(-1, 1) # 重塑X为二维数组
y = data['y'].values
"""
绘制数据散点图
"""
# 绘制散点图
plt.scatter(X, y)
plt.xlabel('X Value')
plt.ylabel('Y Value')
plt.title('Scatter Plot of X vs Y')
plt.show()
# 创建多项式特征(例如,二次多项式)
poly = PolynomialFeatures(degree=8)
X_poly = poly.fit_transform(X)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_poly, y, test_size=0.3, random_state=42)
# 创建并训练模型
model = LinearRegression()
model.fit(X_train, y_train)
# 预测
y_pred = model.predict(X_test)
# 评估模型
mse = mean_squared_error(y_test, y_pred)
print(f"均方误差: {mse}")
# 可选:绘制模型拟合结果
import matplotlib.pyplot as plt
plt.scatter(X, y, color='blue')
plt.plot(X, model.predict(poly.fit_transform(X)), color='red')
plt.title('Non-linear Regression')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
多项式回归的结果如下,本数据集中使用了degree=8(即n=8)均方误差: 107.16818285704927:
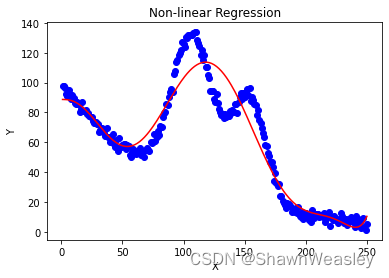
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- python实现文件批量分发
- asp.net core webapi AutoMapper使用
- 20231227在Firefly的AIO-3399J开发板的Android11的挖掘机的DTS配置单后摄像头ov13850
- RPA 是什么?RPA 有哪些功能和用途?
- 【数据结构】线段树算法总结(区间修改)
- 2024.1.23每日一题
- 堆与二叉树(下)
- 据报道,微软的下一代 Surface 笔记本电脑将是其首款真正的“人工智能 PC”
- Spring Boot整合Mybatis配置多数据源
- 2024年【烟花爆竹经营单位主要负责人】考试题库及烟花爆竹经营单位主要负责人最新解析