chisel入门初步1——基4的booth编码的单周期有符号乘法器实现

基4的booth编码乘法器原理说明

基2的booth编码

本质来说就是一个裂项重组，乘法器最重要的设计是改变部分积的数量，另外在考虑有符号数的情况下，最高位符号位有特别的意义。
（注：部分积是指需要最后一起加和的所有部分乘积的项）
下面直接套用其他人图片进行展示，来源如下
https://blog.csdn.net/weixin_42330305/article/details/122868294

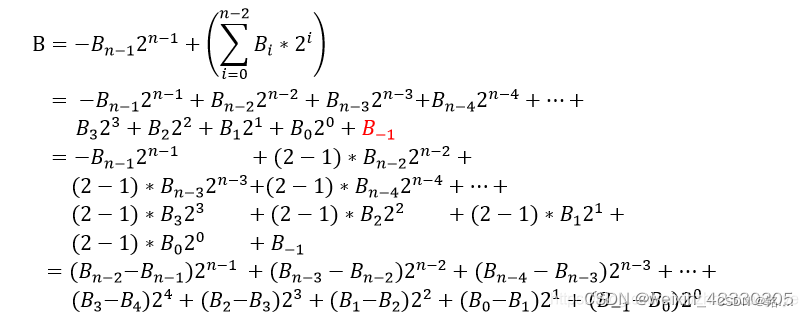
其中$B_{?1}=0$
可以看到，基2的booth编码并没有改变部分积的数量，在实际运行时，基2的booth编码在某些情况下无法提速，甚至可能降速，所以引入基4的booth编码

基4的booth编码

为应对上面问题，这里引入基4的booth编码，将部分积的数量缩小了一半，大大加快了处理速度，具体如下
图片来源与上面相同

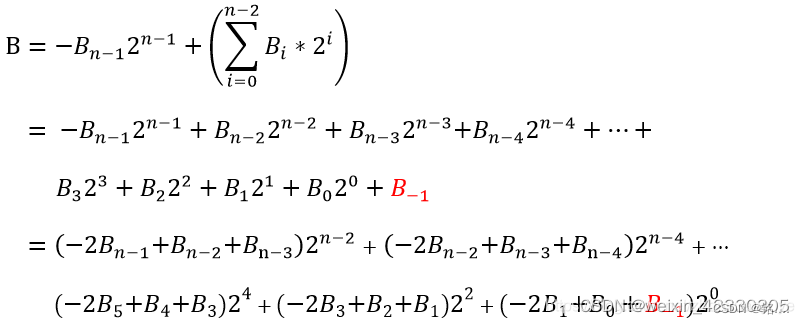
所以

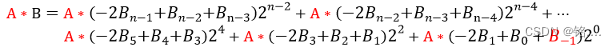
其中$B_{?1}=0$
在实际处理时，为保证形式统一且数组访问时不越界，可以这样处理

b = {B, 0};

通过在末尾拼接一个0，整个式子可以写成下述形式
$A?B={\sum }_{i=0}^{\frac{n}{2}?1}(?2?b_{2i+2}+b_{2i+1}+b_{2i})?2^{2i}?A$
可以看出，部分积的数量减少到原来的一半，乘法器速度大大加快

基4的booth编码的单周期有符号乘法器Verilog实现

直接丢出Verilog代码

/*
* 基4的booth编码的单周期有符号乘法器
*/

module booth_multiplier_base4 #(
    parameter DATA_WIDTH = 8       // 数据位宽应该为2的指数
)

(  
    input [DATA_WIDTH-1 : 0] a,  
    input [DATA_WIDTH-1 : 0] b,  
    output reg [2*DATA_WIDTH-1 : 0] product,
    input clk
);  
  
    integer i;  
    reg [2:0] booth_bits [DATA_WIDTH/2-1:0];  
    reg [DATA_WIDTH:0] b_extended;
    reg [2*DATA_WIDTH:0] partial_product [DATA_WIDTH/2-1:0];  
    reg [2*DATA_WIDTH-1:0] a_pos, a_neg, a_extend; 
  
    always @(posedge clk) begin  
        b_extended = {b, 1'b0}; // 这里我补了个0，防止索引超出界限
        a_extend = {{DATA_WIDTH{a[DATA_WIDTH-1]}}, a};    // 符号位扩展 ，之前忘记扩展找了好久
        a_pos = a_extend;
        a_neg = ~a_extend + 1'b1;  // 补码运算
        product = 0;

        for (i = 0; i < DATA_WIDTH/2; i = i + 1) begin  
            booth_bits[i] = {b_extended[2*i+2], b_extended[2*i+1], b_extended[2*i]};  

            case (booth_bits[i])
            /*
            $\sum_{i=0}^{\frac{n}{2}-1} (-2 \cdot b_{2i+2} + b_{2i+1} + b_{2i})$  // LaTex
            { b(2i+2), b(2i+1), b(2i) } :=
                000:    0;
                001:    1;
                010:    1;
                011:    2;
                100:    -2;
                101:    -1;
                110:    -1;
                111:    0;
            */  
                3'b000, 3'b111: partial_product[i] = 9'd0;  
                3'b001, 3'b010: partial_product[i] = a_pos;
                3'b011:         partial_product[i] = a_pos << 1;
                3'b100:         partial_product[i] = a_neg << 1;
                3'b101, 3'b110: partial_product[i] = a_neg; 
            endcase  
        end

        for (i = 0; i < (DATA_WIDTH/2-1); i = i + 1) begin
            product = product + (partial_product[i] << (2*i)); // Shift and accumulate
        end
            
          

    end  
  
endmodule

testbench如下

`timescale 1ns/1ns

module sim_booth_multiplier_base4 ();

parameter DATA_WIDTH = 8;    

reg [DATA_WIDTH-1:0] a;
reg [DATA_WIDTH-1:0] b;
wire [2*DATA_WIDTH-1:0] product;
reg [2*DATA_WIDTH-1:0] expected_product;
reg test_passed;
reg clk;

booth_multiplier_base4 #(.DATA_WIDTH(DATA_WIDTH)) booth_multiplier_base4_0
(
    .a(a),
    .b(b),
    .product(product),
    .clk(clk)
);

initial begin  
    // 初始化  
    $display("Time, a, b, Expected Product, Actual Product, Test Result\n");  
    clk = 0;
    // 第一个样例  
    a <= 8'b01111111; // 127  
    b <= 8'b00000010; // 2  
    expected_product <= 16'd254; // 254  
    #10; // 等待一些时间以便观察波形  
    test_passed = (product == expected_product) ? 1 : 0;  
    $display("%d, %b, %b, %b, %b, %s\n", $time, a, b, expected_product, product, (test_passed ? "PASSED" : "FAILED"));  

    // 第二个样例 (注意：在实际八位乘法中这是不可能的，因为会溢出)  
    // 我们可以故意让它失败，或者用一个能够处理溢出的乘法器  
    a <= 8'b10000000; // -128 (补码表示)  
    b <= 8'b10000000; // -128 (补码表示)  
    // 由于这个乘法实际上会溢出，所以设置expected_product为一个不可能的值  
    expected_product <= 16'bx0000000000000000; // 'x'表示不关心这些位  
    #10;  
    // 这里我们检查乘法器是否设置了溢出标志位（如果有的话），或者检查最高位是否设置正确  
    // 由于我们没有具体的乘法器实现细节，这里只能做一个假设性的检查  
    // 假设乘法器在溢出时将最高位设置为1  
    test_passed = (product == expected_product) ? 1 : 0;  
    $display("%d, %b, %b, %b, %b, %s (Overflow Expected)\n", $time, a, b, expected_product, product, test_passed ? "PASSED" : "FAILED");  

    // 第三个样例  
    a <= 8'b11111111; // -1  
    b <= 8'b11111111; // -1  
    expected_product <= 16'b0000000000000001; // 1  
    #10;  
    test_passed = (product == expected_product) ? 1 : 0;  
    $display("%d, %b, %b, %b, %b, %s\n", $time, a, b, expected_product, product, test_passed ? "PASSED" : "FAILED");  

    // 结束仿真  
    $finish;  
end  

always begin
    #2;
    clk = ~clk;
end
endmodule

代码不详细讲了，应该还比较清楚，没有进行性能的优化，仅完成功能的实现

基4的booth编码单周期有符号乘法器chisel实现

和Verilog代码逻辑相同，这里直接撇出来
模块代码

import chisel3._  
import chisel3.util._  
  
class BoothMultiplierBase4(val DATA_WIDTH: Int = 8) extends Module {  
  val io = IO(new Bundle {  
    val a = Input(SInt(DATA_WIDTH.W))  // Signed input a  
    val b = Input(SInt(DATA_WIDTH.W))  // Signed input b  
    val product = Output(SInt((2 * DATA_WIDTH).W)) // Signed output product  
  })  
  
  val booth_bits = Wire(Vec((DATA_WIDTH / 2), UInt(3.W)))  
  val partial_products = RegInit(VecInit(Seq.fill(DATA_WIDTH / 2)(0.S((2 * DATA_WIDTH).W))))  
  
  // On every positive edge of the clock  
 
  val b_extended = io.b << 1.U // Sign-extend b with an extra 0  
  val a_neg = -io.a                    // Negation of a  
  val a_pos = io.a                     // Positive of a
  val regProduct = RegInit(0.S((2 * DATA_WIDTH).W))
 
  // Calculate Booth bits  
  for (i <- 0 until DATA_WIDTH / 2) {  
    booth_bits(i) := Cat(b_extended(2*i+2), b_extended(2*i+1), b_extended(2*i)) 

    // Calculate partial products based on Booth encoding  
    partial_products(i) := MuxCase(0.S, Array(  
      (booth_bits(i) === 0.U || booth_bits(i) === 7.U) -> 0.S,  
      (booth_bits(i) === 1.U || booth_bits(i) === 2.U)  -> a_pos,  
      (booth_bits(i) === 3.U) -> (a_pos << 1.U),  
      (booth_bits(i) === 4.U) -> (a_neg << 1.U),                 // 此处自动进行符号位的扩展，下同
      (booth_bits(i) === 5.U || booth_bits(i) === 6.U) -> a_neg  
    ))  
  }  

  // Accumulate partial products to form the final product  

  io.product := partial_products.zipWithIndex.map{
    case (pp, i) => pp << ((2*i).U)
  }.reduce(_+_)

  

}  
  
/* An object extending App to generate the Verilog code*/
object BoothMultiplierBase4 extends App {
  (new chisel3.stage.ChiselStage).emitVerilog(new BoothMultiplierBase4(), Array("--target-dir", "./verilog/BoothMultiplier"))
}

测试代码

import org.scalatest.flatspec.AnyFlatSpec  
import scala.util.Random  
import chisel3._  
import chisel3.tester._  

// Booth乘法器的测试类  

  
class BoothMultiplierBase4Test extends AnyFlatSpec with ChiselScalatestTester {  
    behavior of "BoothMultiplierBase4"  
    
    it should "multiply signed numbers correctly" in {  
        for (i <- 0 until 10) {  
            val a = Random.nextInt(256) - 128 // 生成-128到127之间的随机数  
            val b = Random.nextInt(256) - 128  
    
            test(new BoothMultiplierBase4) { c =>  
                c.io.a.poke(a.S) // 将随机数a作为有符号数输入  
                c.io.b.poke(b.S) // 将随机数b作为有符号数输入  
                c.clock.step(2) // 时钟前进一步以执行乘法  
        
                val expectedProduct = a.toLong * b.toLong // 计算预期乘积  
                val actualProduct = c.io.product.peek().litValue.toLong // 获取实际乘积  
                /* 
                    c: 这是测试环境中BoothMultiplierBase4模块的实例。
                    c.io.product: 这是指向模块输出端口product的引用。
                    peek(): 这是一个Chisel测试方法，用于在不推进时钟的情况下读取端口的当前值。
                    litValue: 这是一个方法，用于从Chisel的Data类型中提取实际的Scala值（在这个例子中是BigInt） 
                */
                
                println(s"Iteration: $i, A: $a, B: $b, Expected Product: $expectedProduct, Actual Product: $actualProduct")  

                assert(actualProduct === expectedProduct, s"Product is incorrect at iteration $i! Expected: $expectedProduct, Actual: $actualProduct")  
        
                
            }  
        }  
    }  
}

测试结果

Iteration: 0, A: -70, B: 110, Expected Product: -7700, Actual Product: -7700
o		# 不知道这个o是哪里来的。。。
Iteration: 1, A: 105, B: 104, Expected Product: 10920, Actual Product: 10920
Iteration: 2, A: 69, B: -90, Expected Product: -6210, Actual Product: -6210
Iteration: 3, A: 62, B: -64, Expected Product: -3968, Actual Product: -3968
Iteration: 4, A: -34, B: -104, Expected Product: 3536, Actual Product: 3536
Iteration: 5, A: -49, B: 103, Expected Product: -5047, Actual Product: -5047
Iteration: 6, A: 57, B: 56, Expected Product: 3192, Actual Product: 3192
Iteration: 7, A: 32, B: 22, Expected Product: 704, Actual Product: 704
Iteration: 8, A: -51, B: -101, Expected Product: 5151, Actual Product: 5151
Iteration: 9, A: -94, B: 54, Expected Product: -5076, Actual Product: -5076