【动态规划】20子数组系列_环形子数组的最大和_C++（medium）

题目链接：leetcode环形子数组的最大和

---

目录

题目解析：

算法原理

1.状态表示

2.状态转移方程

3.初始化

4.填表顺序

5.返回值

编写代码

---

题目解析：

题目让我们求返回?nums?的非空?子数组?的最大可能和?

这道题如果是按照-这道题-是不对的，因为这道题中是环形数组。

这道题我们可以分情况讨论：

1.先按照之前的方法：子数组系列_最大子数组和?

求出如果不是环形数组那么他的最大和是多少；

(求最大和)

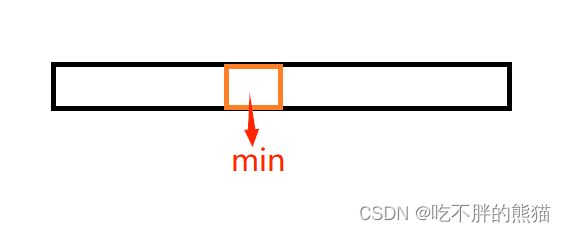
2.我们反过来想，这里题目求和最大值，

如果我们求得这个数组里的连续最小和，再用数组总和-最小和---》就可以得到这个数组的最大和

（求最小和）

---

算法原理:

1.状态表示

先创建一个dp表

首先先思考dp表里面的值所表示的含义（是什么？）

根据上面的分析，我们需要求两中状态的最大和：

f[i] 表示:以i 为结尾的所有子数组中的最大和

g[i] 表示:以i为结尾的所有子数组中的最小和

这种状态表示怎么来的？

1.经验+题目要求

用之前或者之后的状态，推导出dp[i][j]的值；

根据最近的最近的一步，来划分问题

2.状态转移方程

dp[i]等于什么？

?一、(求最大值f[i]):

这里我们分两种情况讨论：

情况一：当连续子数组的长度==1

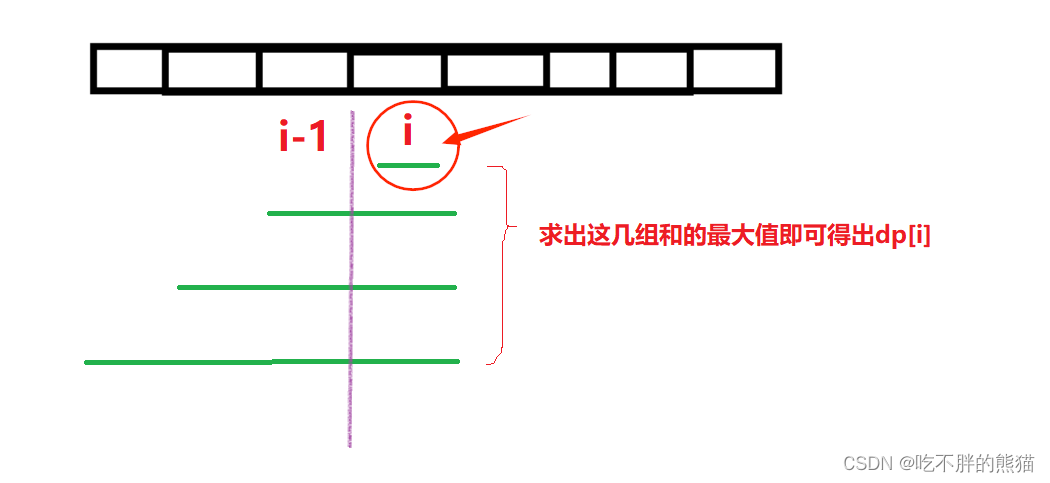
那么此时f[i]就应该等于该位置的值，即num[i];

所以得：f[i]=num[i];

情况一：当连续子数组的长度>1

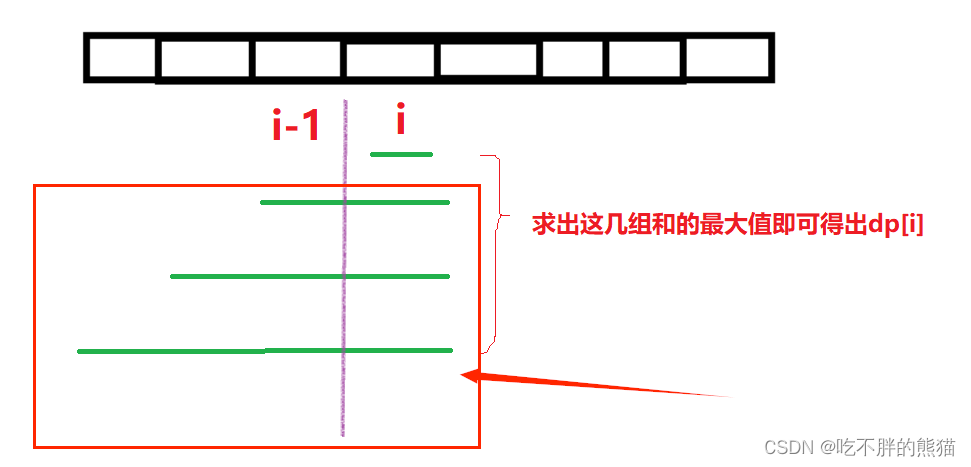
此时我们应该用i-1位置的最大和再加上i位置的值（num[i]），

而“i-1位置的最大和”就是f[i-1]

所以得f[i]=f[i-1]+num[i]

综上：

题目需要最大值，所以要取这两者的最大值：

即：f[i]=max(num[i],f[i-1]+num[i])

一、(求最小值g[i]):

同理g[i]=min(num[i],g[i-1]+num[i])

3.初始化

(保证填表的时候不越界)

根据状态转移方程，我们需要初始化[i-1]

这里我们采用创建虚拟节点的方式：

为了不让f[0]影响后续的值，

所以f[0]=g[0]=0;

4.填表顺序

（为了填写当前状态的时候，所需要的状态已经计算过了）

这里所需要的状态是：

这里所需要的状态是：i-1

所以从左到右

5.返回值

（根据题目要求和状态表示）

综上分析：

如果最小值==数组和，说明该数组中都是负数，

此时只需返回f表里的最大值就可以了

否则就返回数组和-g表里的最小值就可以得到最大值

---

编写代码:

class Solution {
public:
    int maxSubarraySumCircular(vector<int>& nums) {

        //1.创建dp表
        //2.初始化
        //3.填表
        //4.返回结果
        int n=nums.size();
        vector<int> f(n+1);
        auto g=f;

        int rmax=INT_MIN;
        int rmin=INT_MAX;
        int sum=0;
        for(int i=1;i<n+1;i++)
        {
            int x=nums[i-1];
            f[i]=max(x,f[i-1]+x);
            rmax=max(f[i],rmax);

            g[i]=min(x,g[i-1]+x);
            rmin=min(g[i],rmin);

            sum+=nums[i-1];
           
        }
   
        return  sum == rmin ? rmax : max(rmax, sum - rmin);

    }
};