力扣416. 分割等和子集（java 动态规划）

Problem: 416. 分割等和子集

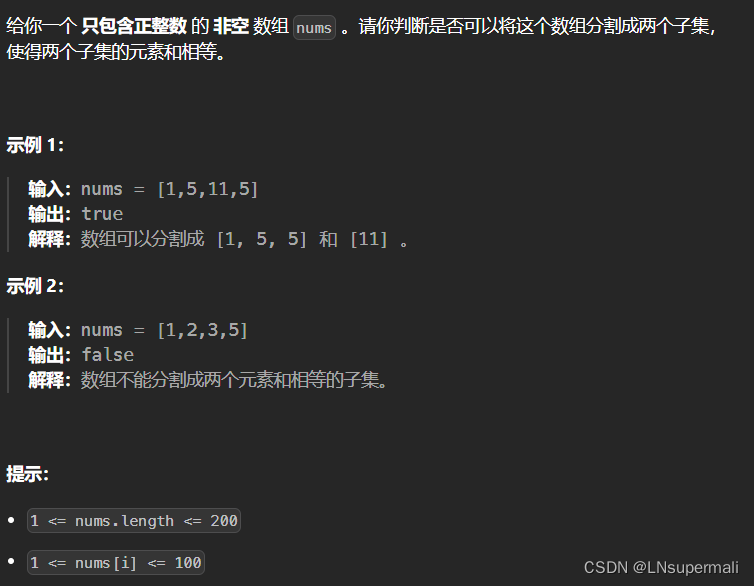
题目描述

思路

该题目可以归类为0-1背包问题，具体到细节可以再归纳为背包是否装满问题

1.首先判断数组元素和的奇偶性（奇数则不能划分）
2.我们定义一个二维布尔类型数组，用于记录每一阶段的可选状态
3.针对于动态转移方程：我们要判断最终是否可以选取一些数使其和为原来数组元素和的一半，即通过一层一层的选择数（状态转移），判断最终状态是否可达（能否有一组数使得其和为原来数组元素和的一半）每一个位置都会有选与不选两种状态，若选取则dp[i][j] == dp[i - 1][j - nums[i]]，若不选取则dp[i][j] == dp[i - 1][j]；则我们可以知道每一个位置的状态只取决于上一层的两个位置的状态即 dp[i][j] == dp[i - 1][j] || dp[i - 1][j - numsi

解题方法

1.获取数组的长度（假设为$n$），统计数组所有元素的和（假设为$sum$）并判断若$sum$为奇数则直接返回false，否则将$sum$除以2；
2.定义一个Boolean类型的二维数组dp（行数为$n$，列数为$sum+1$），用于记录每个状态，初始化（将dp[0][0]位置设置为true），并判断若*nums[0]位置值小于sum(注意sum已经除等于2了)*则将dp[0][nums[0]]位置设为true，这样就将第0层的所有状态设置完毕
3.我们从dp数组的第一层开始遍历，并完成动态转移，在没有越界（此处笔者感觉也不能就叫做越界，但是思想和上述思路中的动态转移是一致的。执行该if判断只是为了更好契合该dp数组。读者可以尝试画一画dp数组演示一边便可理解）的情况下(if (j - nums[i] >= 0))则dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];否则dp[i][j] = dp[i - 1][j];
4.返回最终位置的状态即**dp[n - 1][sum]**位置的状态

复杂度

时间复杂度:

$O(MN)$；其中$M$为数组长度，$N$为数组元素和的一半

空间复杂度:

$O(MN)$；其中$M$为数组长度，$N$为数组元素和的一半

Code

class Solution {
    /**
     * Similar to the 0-1 knapsack problem (can the knapsack be filled?)
     *
     * @param nums Given arrays
     * @return boolean
     */
    public boolean canPartition(int[] nums) {
        int n = nums.length;
        int sum = 0;
        for (int i = 0; i < n; ++i) {
            sum += nums[i];
        }
        //Indivisible if odd
        if (sum % 2 == 1) {
            return false;
        }
        sum /= 2;
        //Records whether each node is reachable
        boolean[][] dp = new boolean[n][sum + 1];
        dp[0][0] = true;
        if (nums[0] <= sum) {
            dp[0][nums[0]] = true;
        }
        //State transition equation
        for (int i = 1; i < n; ++i) {
            for (int j = 0; j <= sum; ++j) {
                //Determine whether the line has been crossed
                if (j - nums[i] >= 0) {
                    dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[n - 1][sum];
    }
}