leetcode深度优先搜索和广度优先搜索总结 Python
目录
一、深度优先搜索
深度优先搜索本质也是暴力遍历法,其遍历的思路是沿着二叉树的分支一直向下遍历,直至最底层,然后回头沿着分支继续遍历。在遍历的同时基于结果的记录顺序的不同,深度优先搜索又可以分为前序遍历、中序遍历和后序遍历,只有前序遍历的遍历顺序与结果记录顺序相同,所以前序遍历的迭代法最清晰明了。
1. 前序遍历
前序遍历的顺序是 中-左-右,本质上是先根节点再子节点的顺序,可以通过递归法和迭代法实现,但递归法的实现思路更加清晰。
(1)递归法
递归法就是函数在函数实现中调用函数本身,但函数实现中还需要增加调用终止条件,在函数实现中可以先假定函数已经实现,所以在考虑一个根节点和两个子节点时,可以直接调用函数本身实现两个子节点的遍历,函数实现中仅仅考虑根节点的遍历和终止条件即可,编程思路一目了然。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
def preorderTraversal(root):
# 递归法
if not root: return []
result = []
def traversal(root):
if not root: return
result.append(root.val) # 先将根节点值加入结果
if root.left: traversal(root.left) # 左
if root.right: traversal(root.right) # 右
traversal(root)
return result(2)迭代法

迭代法是通过栈数据结构实现,栈具有先进后出、后进先出的特点,在 python 中,栈就是 List,进栈是 append() 操作,出栈是 pop() 操作。整体编程思路是从栈中每弹出一个节点就马上放入其右节点和左节点,以此实现深度优先,即先把本节点访问完再考虑其他节点。先右后左放入以此实现 中-左-右 的访问顺序,其寻找顺序与结果顺序一致,所以编程思路比较清晰。
def preorderTraversal(root):
# 迭代法
if not root: return []
stack = [root]
res = []
while stack:
node = stack.pop() # 弹出一个节点
res.append(node.val)
if node.right: stack.append(node.right) # 先右后左放入右节点
if node.left: stack.append(node.left) # 放入左节点,后放先出,所以左节点先弹出
return res2. 中序遍历
中序遍历的顺序是 左-中-右,本质上是先左节点再根节点最后再右节点的顺序,可以通过递归法和迭代法实现,但递归法的实现思路更加清晰。
(1)递归法
def inorderTraversal(root):
result = []
def traversal(root):
if root == None: return
traversal(root.left) # 左
result.append(root.val) # 中序
traversal(root.right) # 右
traversal(root)
return result(2)迭代法
? ? ? ? ? ? ?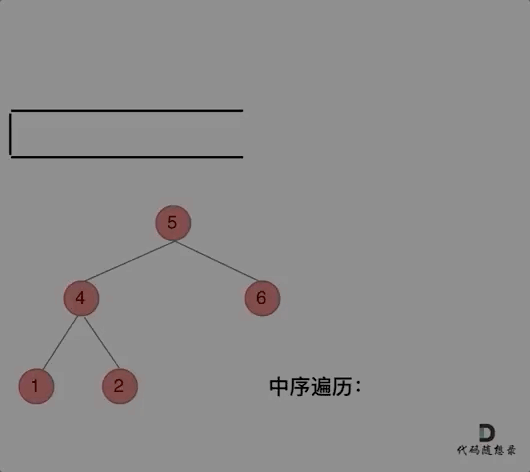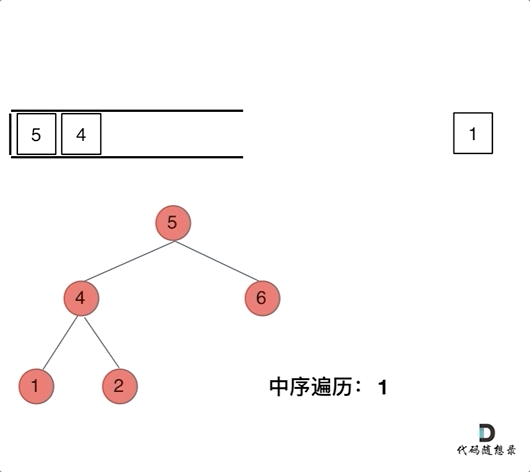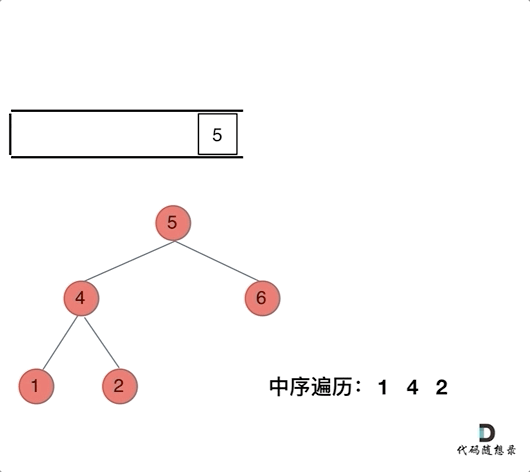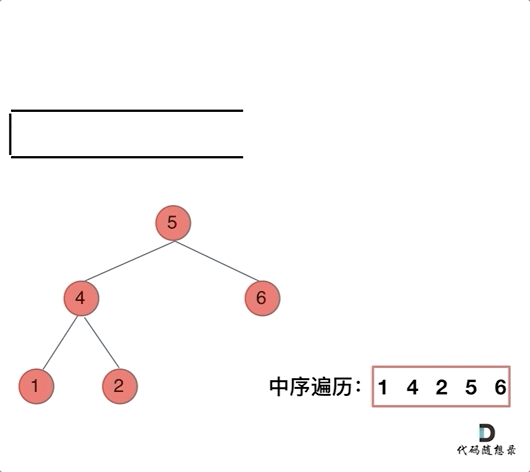
迭代法是通过栈数据结构实现,栈具有先进后出、后进先出的特点,在 python 中,栈就是 List,进栈是 append() 操作,出栈是 pop() 操作。中序遍历的实现思路是先沿着左节点一路向左,到达最左节点后,先访问左节点,再访问根节点,然后遍历右分支。遍历右分支的过程同样是一路向左,然后中,然后右分支。访问完右分支后,退回到最初根节点的上一级节点,再访问右分支。经过上面的分析可以发现,中序遍历的访问过程与结果记录过程是不同步的,前序遍历是同步的,所以在访问的过程中需要一个栈数据结构记录访问的过程,需要一个变量驱动访问过程,需要一个列表记录结果。因为迭代次数是不固定的,所以使用 while 语句,while 的判断条件是 stack 是否为空,但是为了使得第一次迭代能够完成,所以又加入了 cur 的判断条件,所以其实 cur 仅仅在第一次迭代中有效。中序遍历的整体编程思路比较繁琐,比较难理解。
def inorderTraversal(root):
if not root: return [] # 空树
stack = [] # 不能提前将root结点加入stack中
res = [] # 结果list
cur = root
while cur or stack: # cur仅仅正在第一次迭代中起作用,后面不会出现cur为true,stack为false的情况
if cur: # 先迭代访问最底层左子树结点,一路向左
stack.append(cur)
cur = cur.left
else: # 到达最左节点后处理栈顶结点,访问根节点和右分支
cur = stack.pop() # 弹出上一级节点
res.append(cur.val)
cur = cur.right # 取栈顶元素右结点
return res3. 后序遍历
前序遍历的顺序是 左-右-中,本质上是先子节点然后再根节点的顺序,可以通过递归法和迭代法实现,但递归法的实现思路更加清晰。
(1)递归法
def postorderTraversal(root):
# 递归遍历
if not root: return []
result = []
def traversal(root):
if not root: return
traversal(root.left) # 左
traversal(root.right) # 右
result.append(root.val) # 中
traversal(root)
return result(2)迭代法
这里需要知道的是 左-右-中 的访问结果与 中-右-左 的访问结果严格倒序,所以这里只需要对前序遍历的迭代代码进行微调即可实现,微调的内容也就是对进栈顺序调整一下即可。
def postorderTraversal(root):
# 迭代遍历
if not root: return []
stack = [root]
result = []
while stack:
node = stack.pop()
result.append(node.val)
if node.left: stack.append(node.left) # 先左后右
if node.right: stack.append(node.right)
return result[::-1] # 倒序二、广度优先搜索
广度优先搜索本质同样也是暴力遍历法,其遍历的思路是一层一层遍历二叉树,直至最底层。
(1)递归法
这里要求输出一个列表,列表元素数等于二叉树层数,列表中每个元素也是一个列表,每个列表包含对应层的节点值。递归法本质上是深度优先搜索,所以如果要求按照广度优先搜索一个节点一个节点的输出,递归法是不可以的,递归法只能一次性把最终结果输出。因为递归法的原理是搭建一个空的 [[], []..] 的输出结构,然后深度优先遍历二叉树,遍历到的每个节点按照层级向结果数据中填充数据。在递归函数实现中,假定函数已经被实现,那其可以完成左子树和右子树的遍历,那剩余的只需要实现本层的遍历即可,本层的遍历就是将 root 节点按照约定顺序填入结果数据结构中,再搭配终止条件,即完成编程。
def levelOrder(root):
# DFS
def dfs(root, level): # 参数是某节点和对应层数
if not root: return # 终止条件
# 假设 res 是 [[1], [2,3]], level 是 3,就再插入一个 [root.val] 放到 res 中
if len(res) < level: # 结果输出框架
res.append([root.val])
else:
# 将当前节点的值加入到res中,level 代表当前层,假设 level 是 3,节点值是 99
# res 是 [[1], [2,3], [4]],加入后 res 就变为 [[1], [2,3], [4,99]]
res[level-1].append(root.val)
# 递归的处理左子树,右子树,同时将层数 level+1,None会在终止条件中处理
dfs(root.left, level+1) # 深度优先调用
dfs(root.right, level+1)
res = []
dfs(root, 1)
return res(2)迭代法
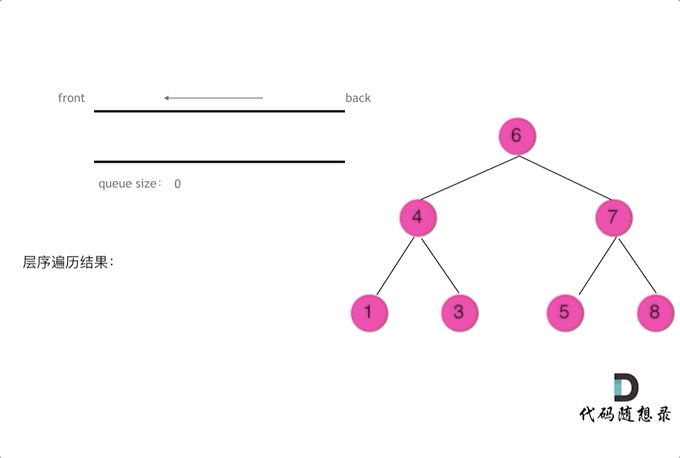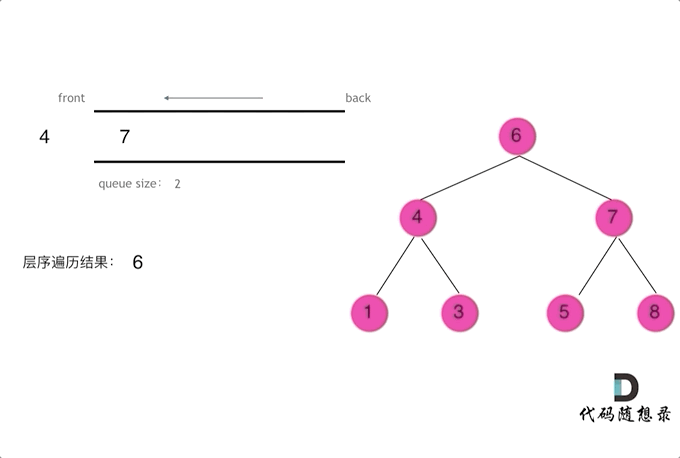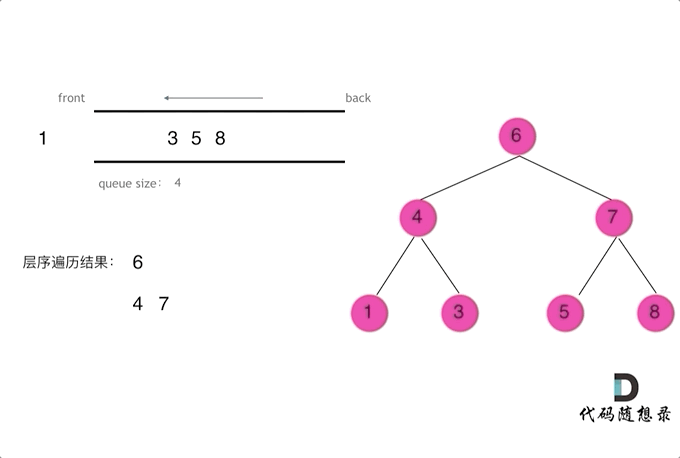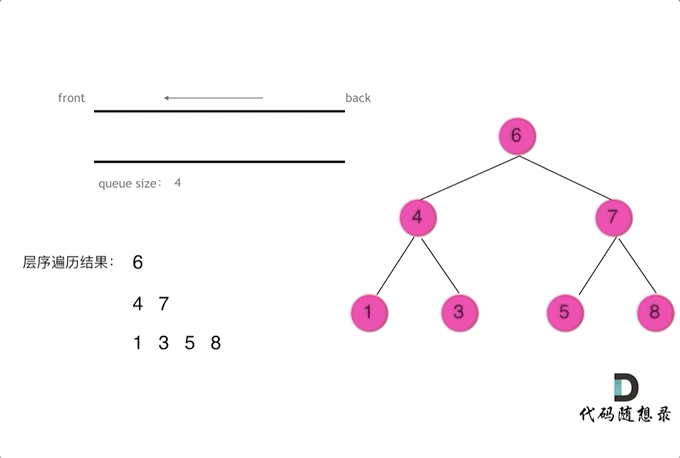
迭代法借由队列数据结构实现,队列具有先进先出、后进后出的属性,在 python 中可以通过?from collections import deque 或者 list + del + append 实现,但是 deque 性能远高于 list,所以这里采用 deque 实现。迭代法的思路其实是以层作为粒度,弹出一层的所有节点,然后放进去下面一层的所有节点,这里需要在注意的是在 que 中我们是无法区分两个节点是否来自于同一层的,所以在编程时,需要实现获取一层的长度。
from collections import deque
def levelOrder(root):
# 二叉树层序遍历迭代解法
if not root: return []
results = []
que = deque([root])
while que:
size = len(que)
result = []
for _ in range(size): # 以层作为粒度进行弹出和输入,这里一定要使用固定大小size,不要使用len(que),因为len(que)是不断变化的
cur = que.popleft()
result.append(cur.val)
if cur.left:
que.append(cur.left)
if cur.right:
que.append(cur.right)
results.append(result)
return results三、例题
1. 记录二叉树每一层的最右节点
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。这个题目需要使用广度优先搜索的迭代实现法,因为该方法可以实现一层一层的访问二叉树的节点,那寻找每一层的最右一个节点并不难
from collections import deque
def rightSideView(root):
if not root: return []
res = []
# deque 相比list的好处是,list的 pop(0) 是 O(n) 复杂度,deque 的 popleft() 是 O(1) 复杂度
que = deque([root])
while que:
res.append(que[-1].val) # 每次都取最后一个node就可以
size = len(que)
for _ in range(size): # 执行这个遍历的目的是获取下一层所有的node
node = que.popleft()
if node.left: que.append(node.left)
if node.right: que.append(node.right)
return res2. 寻找二叉树的最长深度
给定一个二叉树,找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。本问题同样可以借助广度优先搜索中的迭代法,只需要在遍历每一层时 +1 即可统计最长深度。
from collections import deque
def maxDepth(root):
if not root: return 0
que = deque([root])
depth = 0
while que:
size = len(que)
depth += 1
for _ in range(size):
node = que.popleft()
if node.left: que.append(node.left)
if node.right: que.append(node.right)
return depth3. 寻找二叉树的最短深度
给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。该问题既可以借助广度优先搜索的迭代法也可以借助递归法,但在访问每个节点时必须搭配层级参数,对于迭代法此时的遍历粒度不再是层而是节点粒度,判断是都找到最短叶子节点的方式是找到第一次出现某节点无左右子节点。
# 迭代法
import collections
def minDepth(root):
if not root:
return 0
que = collections.deque([(root, 1)])
while que:
node, depth = que.popleft()
if not node.left and not node.right:
return depth
if node.left:
que.append((node.left, depth + 1))
if node.right:
que.append((node.right, depth + 1))
return 0
# 递归法
def minDepth(root):
if not root:
return 0
if not root.left and not root.right:
return 1
min_depth = 10**9
if root.left:
min_depth = min(minDepth(root.left), min_depth)
if root.right:
min_depth = min(minDepth(root.right), min_depth)
return min_depth + 1本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 单元测试(超详细整理)
- <五>Python的基础练习(循环、判断语句)
- 使用C++中的vector容器进行数据排序
- Markdown 通用总结 version 2 - Jan 1st, 2024
- Swift学习笔记第一节:字符串、数字和布尔类型
- iPortal内置Elasticsearch启动失败的几种情况——Linux
- 【React系列】Hook(二)高级使用
- 利用堆来解决数组的topK问题
- 深度探讨 Golang 中并发发送 HTTP 请求的最佳技术
- 力扣热题100道-哈希篇