【动态规划算法(dp算法)】之背包问题
文章目录
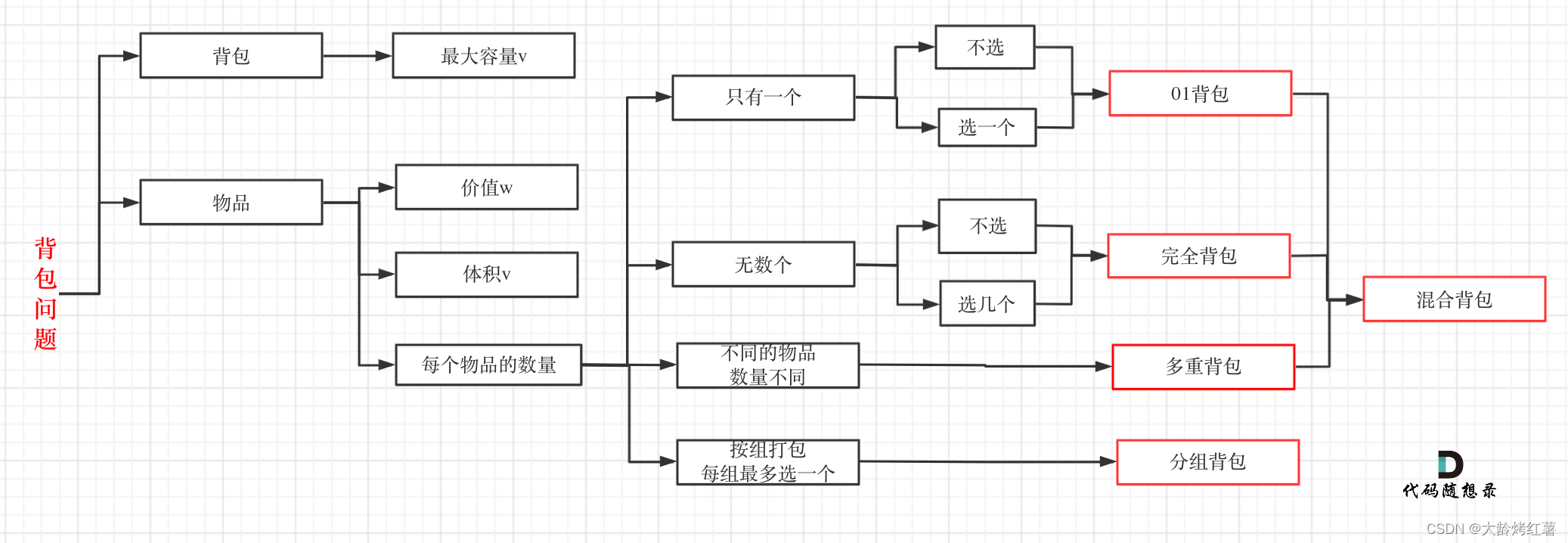
背包问题
动规五部曲
其中最主要的就是前两个步骤
- 确定dp数组以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 遍历顺序
- 出结论,写代码
一、0-1背包问题 :限制物品不可重复 (要么不选 要么选一个)
二、完全背包问题:不限制重复(要么不选 要么可以多选)(完全背包可以转化为0-1背包问题)
下面讲的是0-1背包问题:


其中:
- i,表示物品;j表示背包容量;
- w[] 数组表示物品重量的集合;
- v[] 数组表示物品价值的集合;
- v[][]表示装入背包的最大价值集合;
(1)找w[i]和j的关系
v[i][0]=v[0][j]=0,表示第一列和第一行最大价值都是0;
- 1.w[i]>j,表示当前准备新增物品的质量要是大于背包的容量,v[i][j] =v[i-1][j],该位置的最大价值就是把该列上一行的数据赋给它;如第二次音响进来的最大价值情况;v[i-1][j]上一个单元格装入的最大价值;
- 2.j>=w[i],表示背包的容量要是大于等于当前要新增物品的质量;
(2) 则装入的最大价值策略为:v[i][j] = max { v[i-1][j], v[i] + v[i-1][j-w[i]] }
v[i] 当前商品的价值;
j-w[i] 装入当前物品后,背包剩余的容量大小;
(3) v[i] + v[i-1][j-w[i]]表示:装入当前物品的价值 + 剩余容量可装入的最大价值
最后比较 两个最大价值,取max
eg:总w=4;电脑w=3装入后的价值2000 + 剩余w=1只可装一个吉他价值1500=3500 > 上一个单元格装入的最大价值3000
所以选择这个装配方式;
上面讲的很清楚了 看一下具体的实现
那么可以有两个方向推出来dp[i][j]:
1.不放物品
i:dp[i][j]=dp[i - 1][j]。
w[i]>j,表示:当前准备新增物品的质量要是大于背包的容量,v[i][j] =v[i-1][j],
就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。
2.放物品
i:
表示背包的容量要是大于等于当前要新增物品的质量;
dp[i - 1][j - weight[i]]推出,
dp[i - 1][j - weight[i]]为背包容量为j - weight[i]的时候 不放物品i(所以是i-1)的最大价值value[i]+dp[i - 1][j - weight[i]]
表示:装入当前物品的价值 + 剩余容量可装入的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
动态规划:01背包 二维dp数组
动规五部曲分析一波。
- 确定dp数组以及下标的含义
- 对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0,i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
- w[i] 表示第i个物品的重量;
- v[i] 表示第i个物品的价值;
要时刻记着这个dp数组的含义,下面的一些步骤都围绕这dp数组的含义进行的,如果哪里看懵了,就来回顾一下i代表什么,j又代表什么。
- 确定递推公式
再回顾一下dp [i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
# 那么可以有两个方向推出来dp[i][j]:
##1.不放物品i:dp[i][j]=dp[i - 1][j]。
------w[i]>j,表示当前准备新增物品的质量要是大于背包的容量,v[i][j] =v[i-1][j],
就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。
##2.放物品i:
表示背包的容量要是大于等于当前要新增物品的质量;
# dp[i - 1][j - weight[i]]推出,
dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候 不放物品i(所以是i-1)的最大价值,
# value[i]+dp[i - 1][j - weight[i]]
表示:装入当前物品的价值 + 剩余容量可装入的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
动态规划:01背包滚动数组
读到这里估计大家都忘了 dp[i][j]里的i和j表达的是什么了,i是物品,j是背包容量。
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
动规五部曲分析如下:
-
确定dp数组的定义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为
dp[j]。 -
一维dp数组的递推公式
- dp[j]可以通过dp[j - weight[i]]推导出来:
dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
dp[j - weight[i]] + value[i]表示:容量为 j-物品i重量的背包的价值 加上 物品i的价值。
(就是容量为j的背包,放入物品i了之后的价值再加上物品i的价值) - 此时dp[j]有两个选择:
一个是取自己dp[j]相当于二维dp数组中的dp[i-1][j],即不放物品i;
一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值, - 所以递归公式为:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
- 一维dp数组如何初始化
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么背包容量为0所背的物品的最大价值就是0。
所以dp[0]=0;
假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0就可以了。
Arrays.fill(dp,0);
- 遍历顺序从后向前
? 还是先遍历物品,然后再遍历背包容量
for(int i = 0; i < v.length; i++) { // 遍历物品
for(int j = weight; j >= w[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
}
}
动态规划代码
- 代码
public static void main(String[] args) {
int[] v = {15, 20, 30};
int[] w = {1, 3, 4};
int weight = 4;
int[] dp = new int[weight + 1];
Arrays.fill(dp, 0);
//i是物品 j是背包重量 所以物品重量是w[i]
int res=dp[0];
for (int i = 0; i < v.length; i++) {
for (int j = weight; j >= w[i]; j--) {
dp[j]=Math.max(dp[j],dp[j-w[i]]+v[i]);
res=Math.max(res,dp[j]);
}
}
System.out.println(res);
}
public static void main(String[] args) {
int[] value = new int[]{1500, 2000, 3000};//表示物品的价值
int[] weight = {1, 4, 3};//表示物品的重量
int w = 4;//背包的容量
int n = value.length;//物品的个数
//创建一个二维数组 表 n+1行:有一行是0行;w+1列:有一列是0列
int[][] dp = new int[n + 1][w + 1]; //n+1就是列长 w+1就是行长
//1.初始化第一行第一列
for (int i = 0; i < w + 1; i++) {
dp[0][i] = 0;//第一行为0
}
for (int i = 0; i < n + 1; i++) {
dp[i][0] = 0;//第一列为0
}
int res=dp[0][0];
//2.判断物品重量w[i] 和背包容量的关系
for (int i = 1; i < dp.length; i++) {//从第一行
for (int j = 1; j < dp[0].length; j++) {//第一列开始
if (weight[i-1] > j) {//i-1是因为我们从1开始的
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], (value[i-1] + dp[i - 1][j - weight[i-1]]));
//value[i-1] //是因为我们的i是从1开始的 所以-1
//weight[i-1]
}
res=Math.max(res,dp[i][j]);
}
}
// 3.打印这个最大价值表
for (int i = 0; i <dp.length ; i++) {
for (int j = 0; j <dp[0].length; j++) {
System.out.print(dp[i][j]+"\t");
}
System.out.println();
}
System.out.println("最大价值为:"+res);
}
}
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- 验证时间段区间是否有交叉/重叠
- 天猫数据分析(天猫查数据工具):2023年天猫平台假发行业市场销售数据分析报告
- 2023 英特尔On技术创新大会直播 |我感受到的“芯”魅力
- 小说网站的设计与实现(JSP+java+springmvc+mysql+MyBatis)
- Web Worker:让网页飞起来的幕后英雄(下)
- vcomp120.dll缺失怎么解决,vcomp120.dll丢失的详细修复方法分享(总共5种方法)
- 为uniDBGrid设置文字操作栏
- 解决Typescript报错问题[亲测有效]
- 算法题中常用数学概念、公式、方法汇总(其三:数论)
- adb工具介绍