使用Ray Marching进行3D渲染

要使用Ray Marching渲染 3D 场景，我们需要为每个像素发射一条光线。通过选择屏幕上的一个点（一个像素），并从视点绘制一条射线，我们可以确定它是否击中一个对象，并决定应该在该像素上绘制什么。使用着色器，我们可以并行处理所有像素以完成整个图像。

下面的例子演示了这个想法。 光线的起始位置和方向由视点（眼睛）和当前像素（crd）的位置确定。

vec3 eye = vec3(0.0, 0.0, -2.5);
vec3 rayDir = normalize(vec3(crd, 0.0) - eye);

raymarch 函数是此次演示的主要函数。我们沿光线射线移动一个点并使用 SDF（有符号距离函数）检查它是否足够接近表面。 如果距离低于阈值，该函数将返回距离，否则返回 -1.0。

float raymarch(vec3 eye, vec3 rayDir) {
float dist = 0.0;
float threshold = 0.005;
for(int i = 0 ; i < 16 ; ++i) {
float d = SDF(eye + rayDir * dist);
if(d < threshold) { return dist; }
dist += d;
}
return -1.0;
}

通过下面的codepen示例，我们实现一个raymarch方法，先构建一个半径为0.25的球体，如果光线与该球体相交，就将像素变为白色。
点击查看【codepen】

寻找法线

这是伟大的一步。 然而，球体看起来是平坦的，因为它没有任何阴影。 为了使其看起来更真实，我们需要确定表面的方向（法线）和渲染的每个点的光源。 我们讨论了在照明对象中建模照明的不同方法。 因此，让我们重点关注如何找到计算照明所需的这些因素。

找到光源的方向相当简单，因为随着光线的行进，我们可以很容易地找到它与光线相交的表面的位置。

vec3 P = eye + rayDir * dist;

如果光源可以看作是一个点光源，就像一个小灯泡，我们可以通过从光源的位置减去表面上的位置并对矢量进行归一化来找到方向。 或者，如果光源很远，例如太阳，我们可以假设无论其位置如何，光的方向都保持不变。

为了找到法线，我们可以使用梯度的数值近似方法。 换句话说，通过比较沿每个轴的相邻点的SDF的返回值，我们可以确定距离增加最多的方向。 该方向对应于表面所面向的方向。

vec3 getNormal(vec3 P) {	
	vec3 N;
	vec2 h = vec2(0.001, 0.0);
	N.x	= SDF(P + h.xyy) - SDF(P - h.xyy);
	N.y	= SDF(P + h.yxy) - SDF(P - h.yxy);
	N.z	= SDF(P + h.yyx) - SDF(P - h.yyx);
	return normalize(N);
}

下面的demo使用法线和光线方向来计算兰伯特反射，你可以通过在画布上移动鼠标来更改光源的位置。
点击查看【codepen】

移动物体

在本节中，我们将使用盒子从不同角度提供清晰的透视效果。

float sdBox( vec3 p, vec3 b )
{
  vec3 q = abs(p) - b;
  return length(max(q,0.0)) + min(max(q.x,max(q.y,q.z)),0.0);
}

要平移对象，只需将向量添加到该位置即可。 对于旋转，我们可以使用 2D 旋转矩阵，但我们将使用基于 Rodrigues 旋转公式的函数，公式给出原始向量 v 绕 k 轴旋转 θ 角度的旋转向量 vrot 。

vec3 rotate(vec3 p, float angle, vec3 axis) {
  float s = sin(angle);
  float c = cos(angle);
  float oc = 1.0 - c;
  vec3 n = normalize(axis);
  return p * c + cross(n, p) * s + n * dot(n, p) * oc;
}

点击查看【codepen】
你可能已经注意到，演示demo似乎正在移动光线而不是对象的位置。 这是因为由于位置是相对的，移动射线相当于移动物体。

float SDF(vec3 p) {
	p += vec3(sin(time * PI) * 0.2, 0.0, 0.0); // translation
	p = rotate(p, time * PI, vec3(1.0)); // rotation
	return sdBox(p, vec3(0.2, 0.15, 0.1));
}

下面的演示通过在 z = 0 处分割空间来可视化 SDF 函数的输出。渐变中添加了微弱的条纹，以便更容易看到距离。 当物体移动和旋转时，到物体的距离也会相应变化。
点击查看【codepen】

放置多个对象

我们可以通过取 SDF 的最小值来将多个对象放置在场景中。 让我们首先在 2D 切片中研究这个概念。 仔细观察这个操作对距离梯度的影响。 你可能还会注意到形状重叠时如何无缝地合并在一起。 我们将在讨论形状的布尔运算时进一步探讨这一点。

float SDF(vec3 p) {
	float d = sin(time * PI / 3.0) * 0.125 + 0.25;
	return min(sdOctahedron(p - vec3(d, 0.0, 0.0), 0.2), sdSphere(p + vec3(d, 0.0, 0.0), 0.2));
}

点击查看【codepen】
这是使用 Ray Marching 进行的 3D 渲染。 要为对象分配不同的颜色，我们可以比较与对象的距离以找出射线击中的对象。

vec3 baseColor = sdSphere(P, 0.2) < sdOctahedron(P, 0.2) ? vec3(0.3, 0.6, 1.0) : vec3(1.0, 0.4, 0.5);

点击查看【codepen】

绘制阴影

你是否觉得上一个示例中还有什么地方不对劲？ 当两个物体靠近时看起来有点奇怪，因为它们不应该在彼此身上投射阴影。

当物体阻挡来自光源的光时，表面上会出现阴影。 如果从一点到光源绘制一条线，并且该线与某个对象相交，则从光源看去，该点位于该对象的后面。

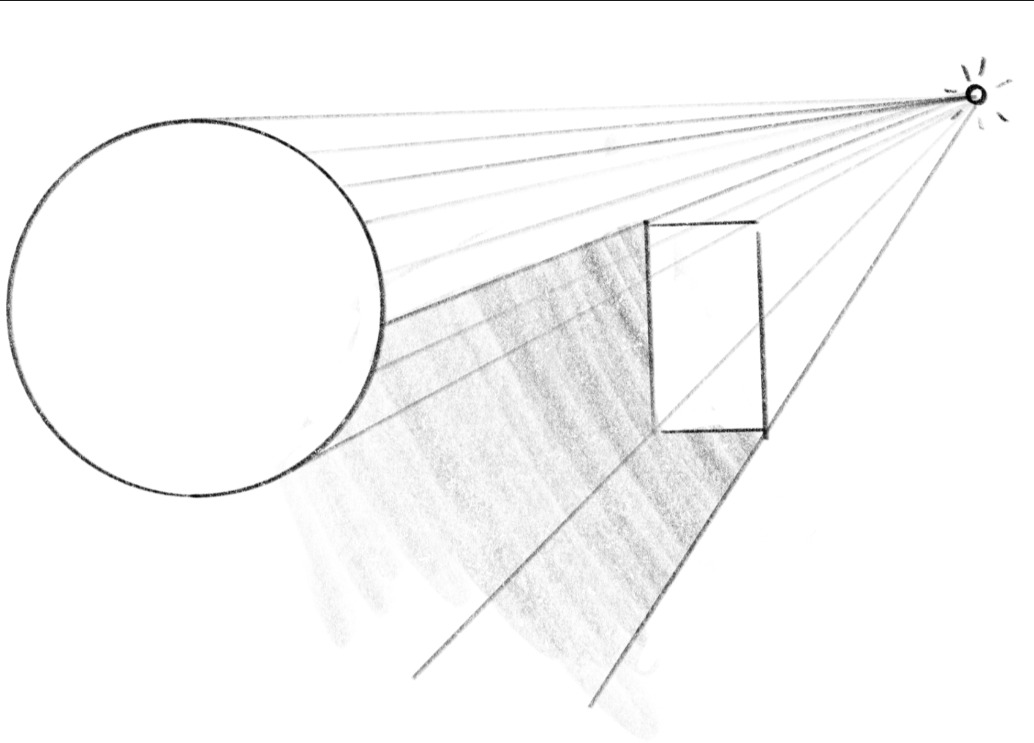
// Take into account shadows
float shadowDist = raymarch(P + 0.001 * N, L);  // Start slightly above the surface to prevent self-shadowing
float shadow = shadowDist >= 0.0 ? 0.0 : 1.0;
Cd *= shadow;

点击查看【codepen】

平行阴影

最后，让我们回顾一下不同类型的投影。 正如我们在上面所看到的，透视投影和平行投影之间的唯一区别在于我们是从单个视点投射光线还是彼此平行投射光线。 在这些模型之间切换只需改变我们设置光线起点和方向的方式即可。 运行下面的演示来查看其实际效果。 可以通过单击画布在两个投影模型之间切换。

vec3 origin, rayDir;
if (parallel) {
	origin = vec3(crd, -2.0);
} else {
	origin = vec3(0.0, 0.0, -2.0);
}
rayDir = normalize(vec3(crd, 0.0) - origin);
float dist = raymarch(origin, rayDir);

点击查看【codepen】