5.5 THREAD GRANULARITY

性能调优中一个重要的算法决定是线程的粒度。有时，在每个线程中投入更多工作并使用更少的线程是有利的。当线程之间存在一些冗余工作时，就会产生这种优势。在当前一代设备中，每个SM的指令处理带宽有限。每个指令都消耗指令处理带宽，无论浮点计算指令、负载指令还是分支指令。消除冗余工作可以减轻指令处理带宽的压力，并提高内核的整体执行速度。

图5.17说明了矩阵乘法的这种机会。图5.6中的tile算法，使用一个线程来计算输出P矩阵的一个元素。这需要一行M和一列N之间的点积。

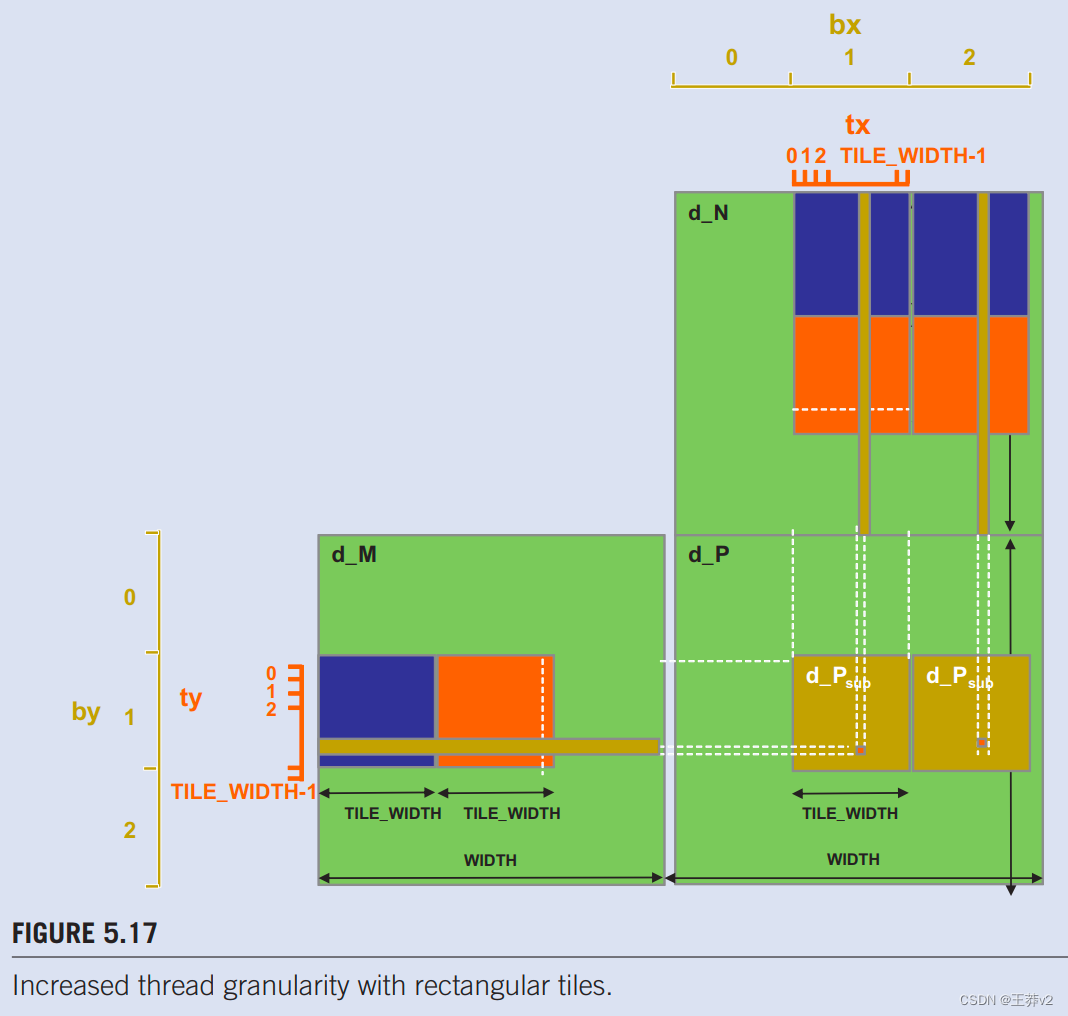
线程粒度调整的机会来自于多个块冗余加载每个M tile的事实。这也在图5.11.中得到了证明。如图5.17所示，相邻 tile 中两个P元素的计算使用相同的 M 行。使用原始的 tile 算法，相同的M行被分配给生成这两个P tile 的两个块冗余加载。人们可以通过将两个线程块合二为一来消除这种冗余。新线程块中的每个线程现在计算两个P元素。这是通过修改内核来完成的，这样两个点积由内核的最内层循环计算。两个点积都使用相同的Mds行，但不同的Nds列。这使全局内存访问减少了四分之一。鼓励读者将新内核作为练习。

潜在的缺点是**，新内核现在使用更多的寄存器和共享内存**。正如我们在上一节中讨论的，可以在每个SM上运行的块数量可能会减少。对于给定的矩阵大小，这也将线程块的总数减少了一半，这可能会导致较小尺寸的矩阵的并行性不足。在实践中，组合多达四个相邻的水平块来计算相邻的水平tile，显著提高了大型（2048x2048或更多）矩阵乘法的性能。