Leetcoder Day12| 二叉树 part02
语言:Java/C++?
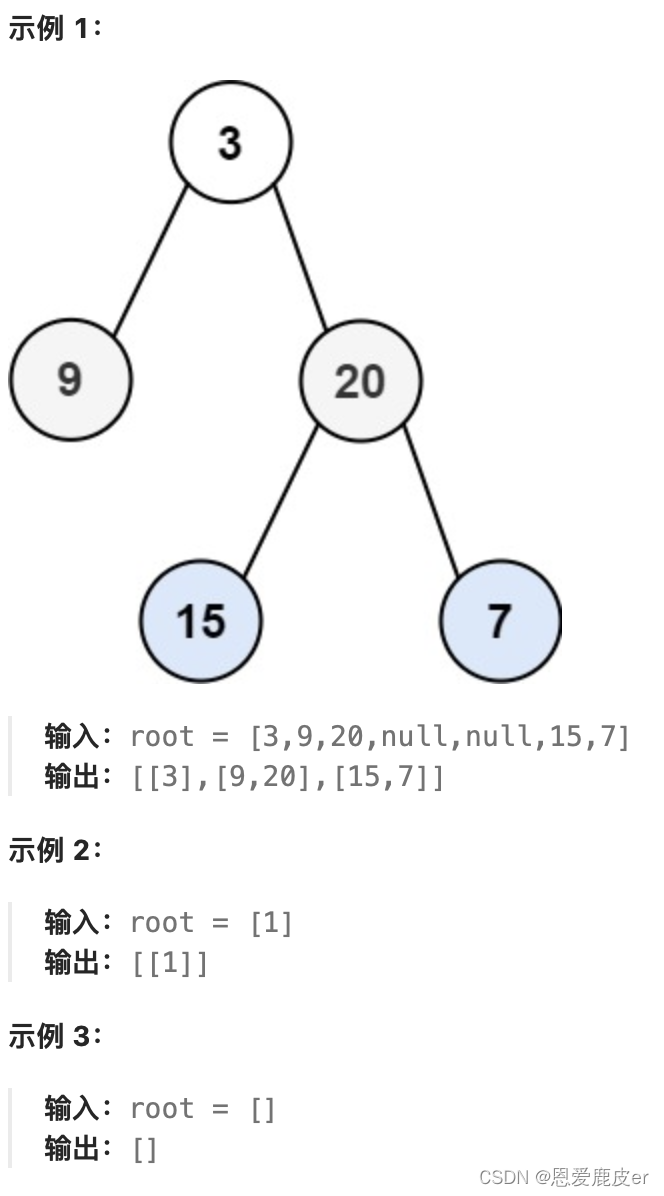
二叉树层序遍历?
给你一个二叉树,请你返回其按层序遍历得到的节点值。 (即逐层地,从左到右访问所有节点)。
在昨天的二叉树理论基础里有提到,层序遍历需要借助队列实现。队列先进先出,符合一层一层遍历的逻辑
class Solution {
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> result= new ArrayList<List<Integer>>();//存放结果
//List<Integer> vec = new ArrayList<>(); 错误写法
Queue<TreeNode> que= new LinkedList<TreeNode>(); //队列
if (root == null) return result;
que.offer(root);
while(!que.isEmpty()){
int len=que.size();
List<Integer> vec = new ArrayList<>();
while(len>0){
TreeNode tmp=que.peek();
que.poll();
vec.add(tmp.val);
if(tmp.left!=null) que.offer(tmp.left);
if(tmp.right!=null) que.offer(tmp.right);
len--;
}
result.add(vec);
}
return result;
}
}vec 列表,导致
vec 列表一直保存了所有层的元素。错误如下:

递归写法:
class Solution {
public List<List<Integer>> result = new ArrayList<List<Integer>>();
public void order(TreeNode root, Integer depth){
if(root==null) return;
depth++; //先进入到下一层好进行判断
if(result.size()<depth){
List<Integer> vec =new ArrayList<>();
result.add(vec);
}
result.get(depth-1).add(root.val);
order(root.left, depth);
order(root.right, depth);
}
public List<List<Integer>> levelOrder(TreeNode root) {
order(root, 0);
return result;
}
}226.翻转二叉树?(优先掌握递归)?
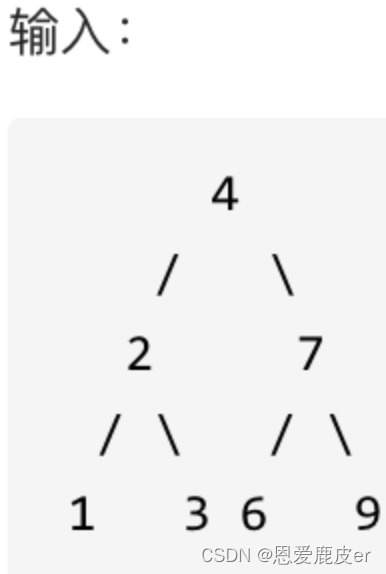
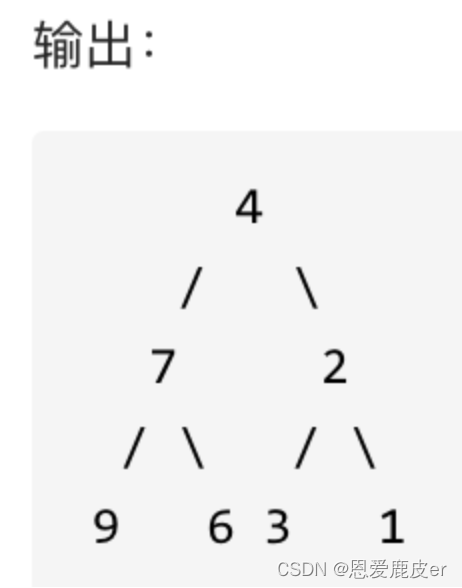
翻转一棵二叉树。
前序遍历的顺序是中左右,因此翻转二叉树可以延续前序遍历或后序遍历,只不过调整一下顺序即可。中序遍历不是很方便。
这里重点还是关注递归写法,考虑三要素:
1. 确定递归函数的参数和返回值
参数就是要传入节点的指针,题目中给出的要返回root节点的指针,可以直接使用题目定义好的函数,所以就函数的返回类型为TreeNode*。
2. 确定终止条件
当前节点为空的时候,就返回
3. 确定单层递归的逻辑
按照中左右的顺序,先进行交换左右孩子节点,然后反转左子树,反转右子树。
class Solution {
public void swap(TreeNode root){
TreeNode tmp=root.left;
root.left=root.right;
root.right=tmp;
}
public TreeNode invertTree(TreeNode root) {
if(root == null) return null;
swap(root);
invertTree(root.left);
invertTree(root.right);
return root;
}
}给定一个二叉树,检查它是否是镜像对称的。
首先想清楚,判断对称二叉树要比较的是哪两个节点,要比较的可不是左右节点!
二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了其实我们要比较的是两个树(这两个树是根节点的左右子树),所以在递归遍历的过程中,也是要同时遍历两棵树。
因此我们需要比较的是两个子树的里侧和外侧的元素是否相等。
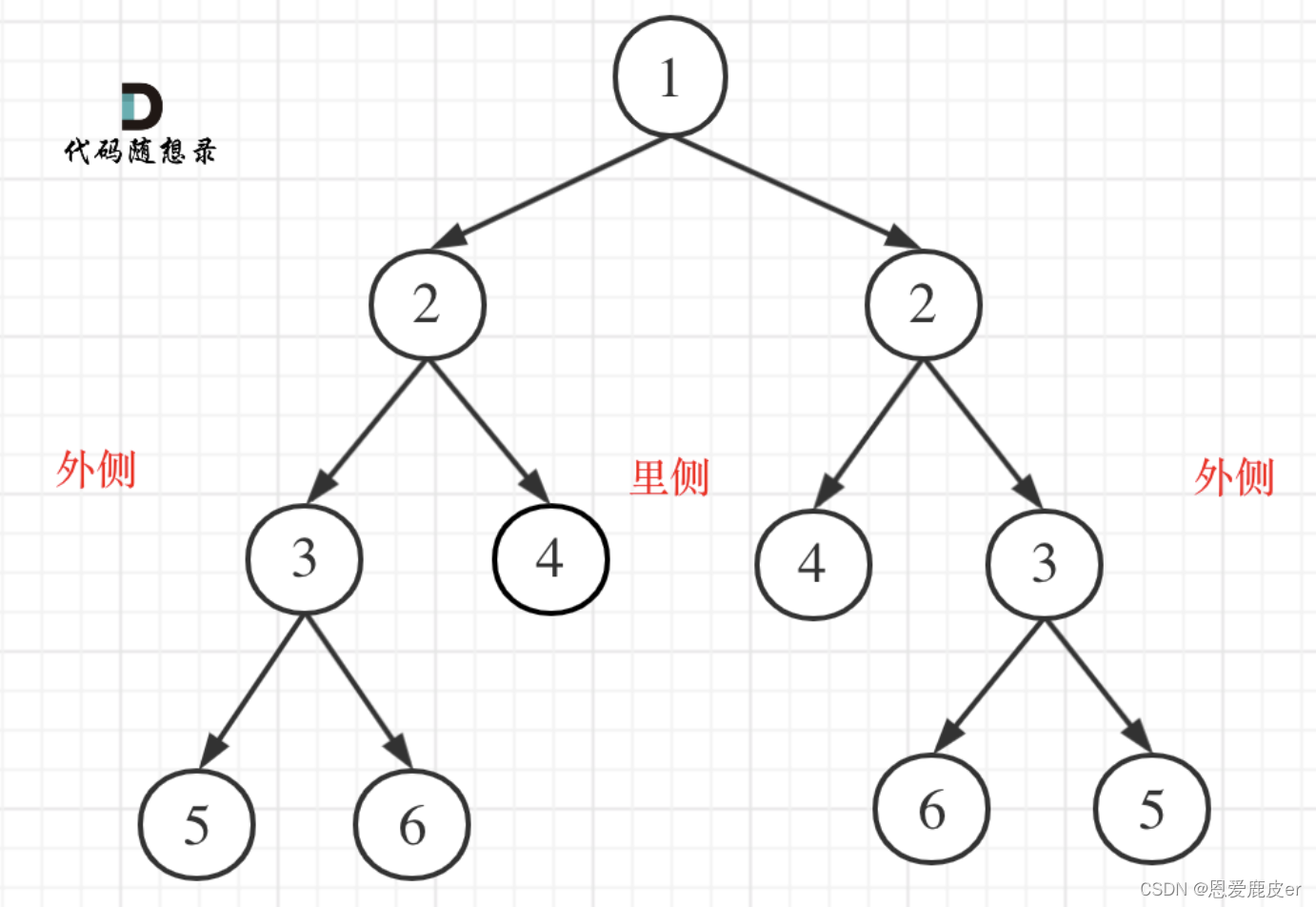
本题遍历只能是“后序遍历”,因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。
正是因为要遍历两棵树而且要比较内侧和外侧节点,所以准确的来说是一个树的遍历顺序是左右中,一个树的遍历顺序是右左中。递归三要素判断如下:
1.?确定递归函数的参数和返回值
因为我们要比较的是根节点的两个子树是否是相互翻转的,进而判断这个树是不是对称树,所以要比较的是两个树,参数自然也是左子树节点和右子树节点。返回值自然是bool类型。
2.?确定终止条件
要比较两个节点数值相不相同,首先要把两个节点为空的情况弄清楚!否则后面比较数值的时候就会操作空指针了。
节点为空的情况有:(注意我们比较的其实不是左孩子和右孩子,所以如下我称之为左节点右节点)
- 左节点为空,右节点不为空,不对称,return false
- 左不为空,右为空,不对称 return false
- 左右都为空,对称,返回true
此时已经排除掉了节点为空的情况,那么剩下的就是左右节点不为空:
- 左右都不为空,比较节点数值,不相同就return false
此时左右节点不为空,且数值也不相同的情况我们也处理了。
3. 确定单层递归的逻辑
此时进入单层递归的逻辑,单层递归的逻辑就是处理 左右节点都不为空,且数值相同的情况。
- 比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
- 比较内侧是否对称,传入左节点的右孩子,右节点的左孩子。
- 如果左右都对称就返回true ,有一侧不对称就返回false 。
class Solution {
public boolean compare(TreeNode left, TreeNode right){
/*
左节点为空,右节点不为空,不对称,return false
左不为空,右为空,不对称 return false
左右都为空,对称,返回true
左右都不为空,比较节点数值,不相同就return false
*/
if(left==null && right!=null) return false;
else if(left!=null && right ==null) return false;
else if(left==null && right==null) return true;
else if(left.val!=right.val) return false;
/*
比较二叉树外侧是否对称:传入的是左节点的左孩子,右节点的右孩子。
比较内侧是否对称,传入左节点的右孩子,右节点的左孩子。
如果左右都对称就返回true ,有一侧不对称就返回false 。
*/
else return compare(left.left, right.right) && compare(left.right, right.left);
}
public boolean isSymmetric(TreeNode root) {
if(root==null) return true;
return compare(root.left, root.right);
}
}本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Javaweb之SpringBootWeb案例员工管理之删除员工的详细解析
- 计算机网络的7层协议和4层协议的区别
- 飘扬的爱意--花费三天用HTML5做三个告白气球
- 互联网加竞赛 python 机器视觉 车牌识别 - opencv 深度学习 机器学习
- RocketMQ系统性学习-RocketMQ原理分析之Broker接收消息的处理流程
- TCP/IP 网络模型
- 代码随想录算法训练营Day25|216.组合总和III、17.电话号码的字母组合
- MySQL取出N列里最大or最小的一个数据
- 软件测试|如何在Pycharm中配置文件头部信息
- vue的slot插槽详解