代码随想录day25 回溯算法加强练习

216.组合总和III

题目

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

• 所有数字都是正整数。
• 解集不能包含重复的组合。

示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]

示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]

思考

这题其实和组合那一题很像，不同的点是把n变成了9，本题中的n其实对应的是函数入参中的sum，这个至关重要，我也是卡在了这里，其实只要传一个参数sum，然后在纵向递归for循环时不停加这个sum就行，中止条件也是sum==n时，res会push_back?path.

代码

class Solution {

public:

? ? vector<vector<int>> res;

? ? vector<int> path;

? ? void backTracking(int k, int n, int startIndex, int sum) {

? ? ? ? if(path.size() == k) {

? ? ? ? ? ? if(sum == n) {//中止有两个条件，path的size等于k，相加之和等于n

? ? ? ? ? ? ? ? res.push_back(path);

? ? ? ? ? ? ? ? return;

? ? ? ? ? ? }

? ? ? ? }

? ? ? ? for(int j = startIndex; j <= 9; j++) {

? ? ? ? ? ? sum += j;

? ? ? ? ? ? path.push_back(j);

? ? ? ? ? ? backTracking(k,n,j+1,sum);

? ? ? ? ? ? sum -= j;//回溯时要弹出元素，所以sum要减j，此时的j等于startIndex

? ? ? ? ? ? path.pop_back();

? ? ? ? }

? ? }

? ? vector<vector<int>> combinationSum3(int k, int n) {

? ? ? ? backTracking(k,n,1,0);

? ? ? ? return res;

? ? }

};

17.电话号码的字母组合

题目

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

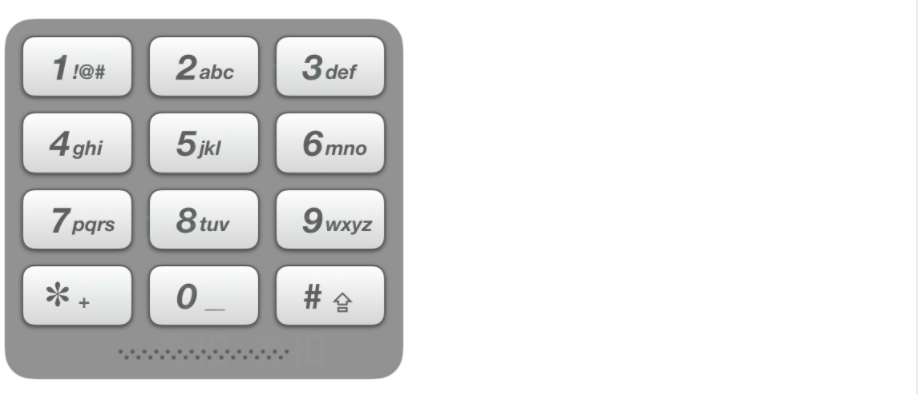
示例:

• 输入："23"
• 输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

说明：尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

思考

这题其实不难，就是有点烦，其实用的还是组合那一题的逻辑，但是有些许不同，下面总结步骤如下：

1、要把数字和字母表给对应起来，怎么对应呢，用一个string数组或者vector<string>来存放：{"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}，然后每个数字就相当于数组里的下标

2、根据1我们可以看出，这里每个数字都代表一个集合，和组合题目不一样，所以这题不需要清除重复项，没有startIndex，参数里只需要有一个index表示遍历到那个数字了即可

3、判断中止条件，这里可以判断index == digits.size() ，也可以当path.lenth == digits.size()

4、找到digits里每个数字对应的字符串

5、横向遍历，注意这里其实就是遍历每个数字对应字符串里的字符，因为path是由digits每个数字对应的字符串取一个字符组成的

6、纵向遍历，递归向下遍历，每个数字对应的字符串取一个字符

7、回溯，path.pop_back()

代码

class Solution {

private:

? ? const string lettersMap[10] = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};

public:

? ? vector<string> res;

? ? string path;

? ? void backtTracking(int k, const string& digits, int index) {

? ? ? ? if(path.length() == k) {

? ? ? ? ? ? res.push_back(path);

? ? ? ? ? ? return;

? ? ? ? }

? ? ? ? int digit = digits[index] - '0';//把字符串digit每一个字符都转化成数字

? ? ? ? string letters = lettersMap[digit];//if digit == 2， letters = “abc”

? ? ? ? for(int i = 0; i < letters.size(); i++) {//遍历letters，把每一个字符都存入path

? ? ? ? ? ? path += letters[i];

? ? ? ? ? ? backtTracking(k, digits, index+1);

? ? ? ? ? ? path.pop_back();

? ? ? ? }

? ? }

? ? vector<string> letterCombinations(string digits) {

? ? ? ? if(digits.size() == 0) return res;

? ? ? ? backtTracking(digits.size(), digits, 0);

? ? ? ? return res;

? ? }

};