343. 整数拆分
发布时间:2024年01月05日
原题链接:
https://leetcode.cn/problems/integer-break/description/
完成情况:
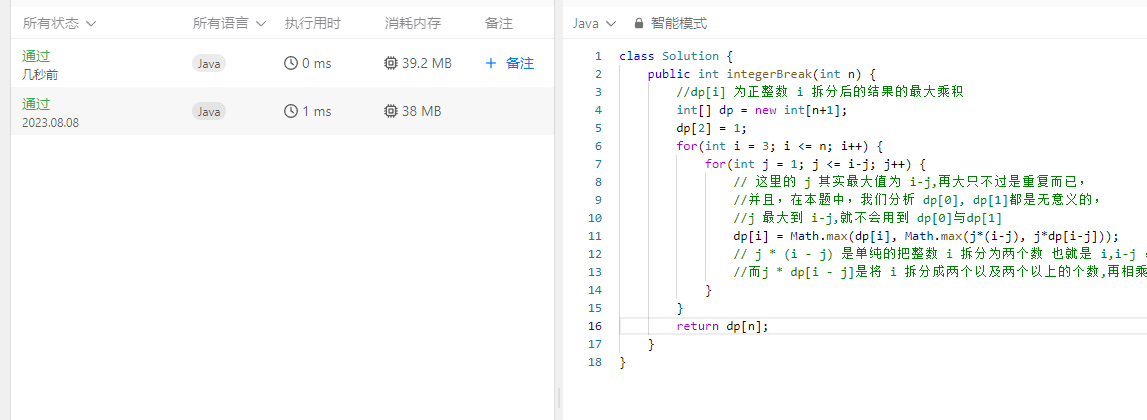
解题思路:
/**
解题思路:
如何使面积最大呢? -> 毫无疑问,肯定是正方形
那么每次我就尝试以均等切分,保存当前的合,
然后迭代求和最大值和最小值,产生一个新的均值
举例:
10
5*5 ->25
5*3*2 ->30
【5和2合并再均分】
4*3*3 ->36
【4和3合并再均分】,与前面【5和2合并再均分】产生的合相同,故结束。
Max算计算过得哪个值最大。
*/
参考代码:
_343整数拆分_拆分法
package 代码随想录.动态规划;
public class _343整数拆分_拆分法 {
public int integerBreak(int n) {
//2 <= n <= 58
//只要前一个结果,跟后一个结果有关系的题目 ,基本上都可以使用到dp
int dp_splitMaxArea [] = new int[n+1];
//2 <= n <= 58
/**
解题思路:
如何使面积最大呢? -> 毫无疑问,肯定是正方形
那么每次我就尝试以均等切分,保存当前的合,
然后迭代求和最大值和最小值,产生一个新的均值
举例:
10
5*5 ->25
5*3*2 ->30
【5和2合并再均分】
4*3*3 ->36
【4和3合并再均分】,与前面【5和2合并再均分】产生的合相同,故结束。
Max算计算过得哪个值最大。
*/
for (int i=2;i<=n;i++){
int curMax = 0;
for (int j=1;j<i;j++){
curMax = Math.max(curMax,Math.max(j*(i-j),j * dp_splitMaxArea[i-j]));
}
dp_splitMaxArea[i] = curMax;
}
return dp_splitMaxArea[n];
}
}
_343整数拆分
package 代码随想录.动态规划;
public class _343整数拆分 {
/**
*
* @param n
* @return
*/
public int integerBreak(int n) {
//dp[i] 为正整数 i 拆分后的结果的最大乘积
int[] dp = new int[n+1];
dp[2] = 1;
for(int i = 3; i <= n; i++) {
for(int j = 1; j <= i-j; j++) {
// 这里的 j 其实最大值为 i-j,再大只不过是重复而已,
//并且,在本题中,我们分析 dp[0], dp[1]都是无意义的,
//j 最大到 i-j,就不会用到 dp[0]与dp[1]
dp[i] = Math.max(dp[i], Math.max(j*(i-j), j*dp[i-j]));
// j * (i - j) 是单纯的把整数 i 拆分为两个数 也就是 i,i-j ,再相乘
//而j * dp[i - j]是将 i 拆分成两个以及两个以上的个数,再相乘。
}
}
return dp[n];
}
}
错误经验吸取
文章来源:https://blog.csdn.net/weixin_43554580/article/details/135403887
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Leetcode算法系列| 9. 回文数
- 网站高性能架构设计——高性能数据库集群
- 如何在Docker中搭建MinIO容器并实现无公网ip远程访问本地服务
- 【C语言期末】基于VS2022的学生成绩管理系统
- php创建临时文件
- loading stable diffusion model: FileNotFoundError解决方案
- javacv和opencv对图文视频编辑-常见错误汇总
- 【Kotlin】Kotlin的stream流编程浅析
- Google Analystics账号的创建
- Java编程案例(专题)