抽奖机制模型及算法

抽奖机制

连抽保底概率模型+不中概率加大模型（抽卡保底）

抽奖概率为n%，在达到某次次数后，每次概率比上次高m%，直至达到保底次数（概率累加和为100%），当抽到极品道具时候，会从奖池中随机抽选，因为是专属抽奖，所以如果本次摸鱼随机到专属，则下次必是专属
拿原神举例来说：
在[1,73]抽时，五星角色的概率为0.6%，在[74，90]次抽时，每次抽卡概率会比上次概率高6%，当获取五星角色时，会有50%的概率获取UP角色，若本次没有抽到UP角色，则下次五星角色必定是UP角色。根据该算法，则第90次达到保底，UP角色则为180次

根据抽奖人数固定比例奖品数量概率模型（逢几中奖）

假设卡A为100人才能有1人拥有，需要计算抽奖总数人，玩家进行抽奖需计算总的抽奖次数，对其进行取余100，得到指定的数，即为抽中
放到现实中，类似于第几个进门的顾客会享受福利

稀有物品最后抽到模型

例如此次抽奖用户只能进行3次抽奖，那最稀有的几种卡，在后几次进行抽奖，必定抽到，前几次抽奖为普通几率权重的1/n

纯随机模型

不进行任何代码影响，只使用随机来进行概率

抽奖算法

洗牌算法

类似于音乐播放器的随机播放，将奖品数组打乱，依次发放？

区间算法

把权重分组，比如有权重是1，2，3。给这权重累计计算总权重，分配空间，空间1是第一个物品，空间2-3是第二个物品，空间3-6是第三个物品，被用户抽到，需要进行删除该空间，比如用户1抽到了1，则现在空间变为空间1-2为第二个物品，空间2-5是第三个物品，如下图：

离散算法（区间算法优化？）

把概率分区分组，利用随机数产生随机概率，加入数组并且排序，比如有概率为：P1=0.2,P2=0.2,P3=0.3,P4=0.3。那么概率区段数组为[0.2，0.4，0.7，1.0]。产生随机数根据区间进行返回具体道具，如下图：

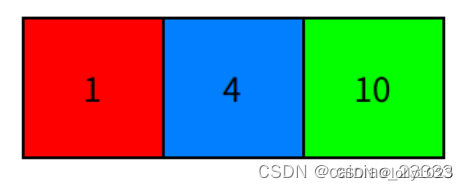
Alias 算法

比较抽象，是离散算法的进一步，把离散算法中的数据改为Alias Table，生成一个宽度为一的矩形，然后把原数据进行伸缩，至完全融入矩形中。

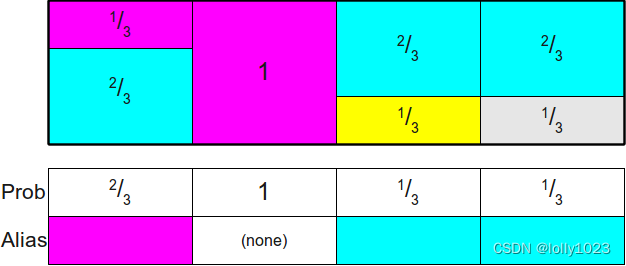
然后进行随机即可，[1,4]如果是2，则有可能会1/3的概率失败，因为有空的存在。这样的时间复杂度，最坏的情况下可能是无限。
这样的话，会有些地方多出一块矩形，或者少一部分矩形，我们需要把多出的部分放置在缺少的部分中，直至全部修改完毕，如果总概率为1则塞满，如果概率不满1，则会有空缺为null。但是每一列至多存在两个事件，不然的话又会回到之前的逻辑中，最后结果为：

依赖不可控的物理随机数 （感觉类似于毒的抽签）