【动态规划】24子数组系列_最长湍流子数组_C++

题目链接：最长湍流子数组

---

目录

题目解析：

算法原理

1.状态表示

2.状态转移方程

3.初始化

4.填表顺序

5.返回值

编写代码

---

题目解析：

题目让我们求返回?arr?的?最大湍流子数组的长度?

由题可得：

如果比较符号在子数组中的每个相邻元素对之间翻转，则该子数组是?湍流子数组;

---

算法原理:

1.状态表示

先创建一个dp表

首先先思考dp表里面的值所表示的含义（是什么？）

这里我们需要两个dp表：

f[i]:以i位置为结尾，i位置为“上升”的最大湍流子数组的长度

g[i]:以i位置为结尾，i位置为“下降”的最大湍流子数组的长度

这种状态表示怎么来的？

1.经验+题目要求

用之前或者之后的状态，推导出dp[i][j]的值；

根据最近的最近的一步，来划分问题

经验：以i位置为结尾；

题目让我们返回?arr?的?最大湍流子数组的长度?，

所以我们可以先设一个“dp表”表示以i位置为结尾，i位置最大湍流子数组的长度。

但是我们会发现：

只有一个dp表无法表示该位置的状态，状态分得还不够细（是>还是<）

所以这里我们尝试再加一个状态表示：

f[i]:以i位置为结尾，i位置为“上升”的最大湍流子数组的长度

g[i]:以i位置为结尾，i位置为“下降”的最大湍流子数组的长度

2.状态转移方程

dp[i]等于什么？

以i位置为结尾有三种情况：

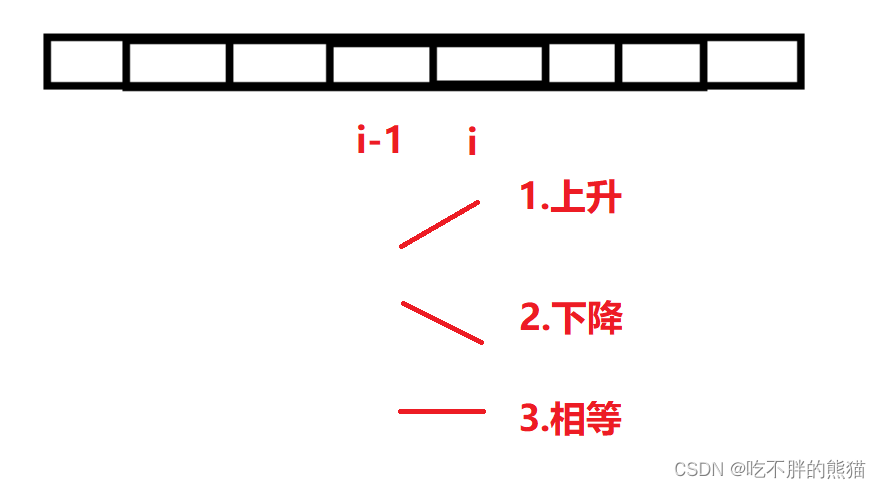
只有是情况1和2时才有可能时湍流子数组；

根据我们的状态表示：

情况一（i位置为“上升”）：

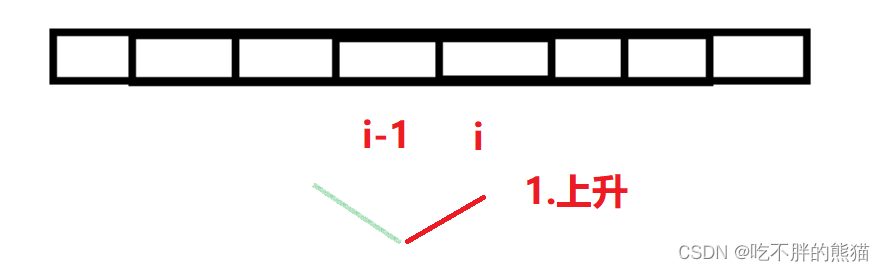
那么需要前面一个位置是“下降”的才满足湍流子数组；

所以此时i位置的最长湍流子数组应该是前面一个位置为“下降”的最长湍流子数组的长度+1；

而“前面一个位置为“下降”的最长湍流子数组的长度”就是我们的状态表示：g[i-1]

所以：f[i]=g[i-1]+1

情况二（i位置为“下降”）：

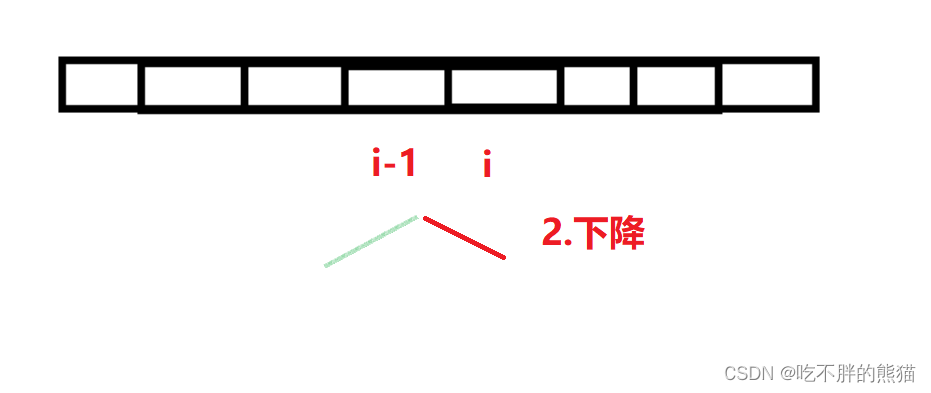
那么需要前面一个位置是“上升”的才满足湍流子数组；

所以此时i位置的最长湍流子数组应该是前面一个位置为“上升”的最长湍流子数组的长度+1；

而“前面一个位置为“上升”的最长湍流子数组的长度”就是我们的状态表示：g[i-1]

所以：g[i]=f[i-1]+1

3.初始化

(保证填表的时候不越界)

我们是从第二个元素比的，所以把要把前面的都初始化为1

4.填表顺序

（为了填写当前状态的时候，所需要的状态已经计算过了）

这里所需要的状态是：[i-1]

所以填表顺序从左往右

5.返回值

（根据题目要求和状态表示）

综上分析：

返回值为：两个表里的最大值

---

编写代码:

class Solution {
public:
    int maxTurbulenceSize(vector<int>& arr) {
        //1.创建dp表
        //2.初始化
        //3.填表
        //4.返回结果

         int n=arr.size();
        vector<int> f(n+1,1);
        auto g=f;

        int ret=1;
        for(int i=2;i<n+1;i++)
        {
            if(arr[i-1]>arr[i-2])
            {
                f[i]=g[i-1]+1;
            }
            else if(arr[i-1]<arr[i-2])
            {
                g[i]=f[i-1]+1;
            }
            ret=max({(int)ret,g[i],f[i]});

        }
        return ret;
    }
};