【深度强化学习】策略梯度方法：REINFORCE、Actor-Critic

参考 
Reinforcement Learning, Second Edition  
An Introduction 
By Richard S. Sutton and Andrew G. Barto

非策略梯度方法的问题

之前的算法，无论是 MC，TD，SARSA，Q-learning， 还是 DQN、Double DQN、Dueling DQN，有至少两个问题：

1. 都是处理离散状态、离散动作空间的问题，当需要处理连续状态 / 连续动作的时候，如果要使用这些算法，就只能把状态 / 动作离散化处理，这会导致实际相邻的 $Q(s,a)$ 的值没有联系，变化不光滑，并且随着离散空间变大，max 的比较操作需要的计算量增大，这导致不能把离散化的分辨率无限地增高。
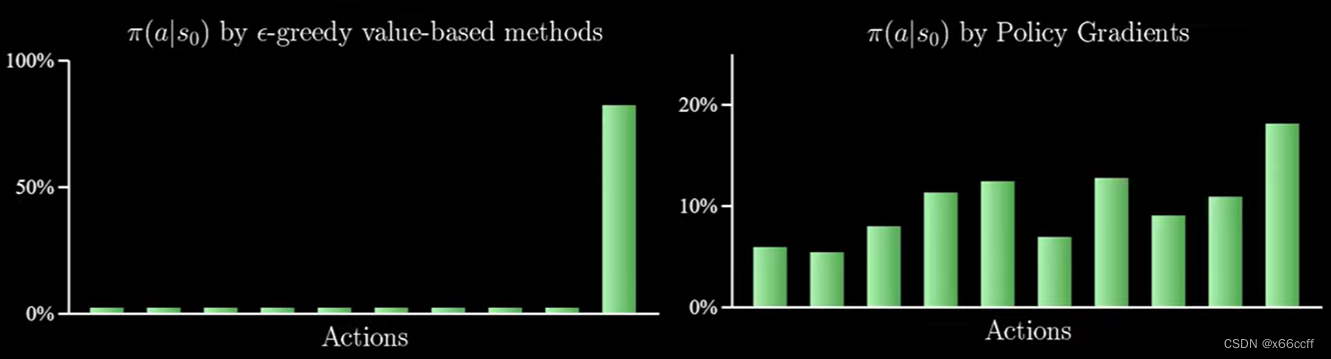
2. 都利用对 $V_{\pi }$ 或 $Q_{\pi }$ 取 ${\mathrm{argmax}}_a$ 来得到策略 $\pi$，会导致只会选最优的动作，尽管有次优的动作，算法也不会去选，只会选最好的，在某些需要随机性的场景（如：非完全信息博弈（军事、牌类游戏））会产生大问题，因为行为比较有可预测性，很容易被针对。（即使有 $?$-贪心）

在非完全信息的纸牌游戏中，最优的策略一般是以特定的概率选择两种不同玩法，例如德州扑克中的虚张声势

策略梯度

策略梯度可以同时解决以上两个问题。
我们将策略参数化为 $\pi (a|s,\theta )$（可以是简单的线性模型+softmax，也可以是神经网络），这个策略可以被关于$\theta$求导：${?}_{\theta }\pi (a|s,\theta )$，简写为 $?\pi (a|s)$

策略梯度的直觉

我们实际上想找到一个更新策略 $\pi (a|s,\theta )$ 的方法，它在$\theta$参数空间里面：

• 如果往一个方向走，能对给定的$(s_t,a_t)$获得正的回报$G_t$，就往这个方向走，并且回报绝对值越大走的步子越大
• 如果往一个方向走，能对给定的$(s_t,a_t)$获得负的回报$G_t$，就不往这个方向走，并且回报绝对值越大走的步子越大

和梯度下降类似，可以得到：
$${\theta }_{t+1}\leftarrow {\theta }_t+\alpha G_t?\pi (a_t|s_t)$$

除以 $\pi$ 变成 Ln

单纯这样更新会有问题，因为如果$\pi$被初始化为存在一个次优动作（具有正回报），并且概率很大，而最优动作的概率很小，那么这个次优动作就很可能被不断地强化，导致无法学习到最优动作。

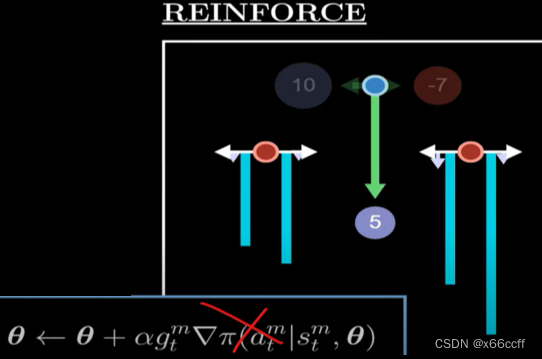
因此我们要除一个动作的概率，得到修正后的版本：

$${\theta }_{t+1}\leftarrow {\theta }_t+\alpha G_t\frac{?\pi (a_t|s_t)}{\pi (a_t|s_t)}$$

也就是
$${\theta }_{t+1}\leftarrow {\theta }_t+\alpha G_t?\ln \pi (a_t|s_t)$$

REINFORCE

如果这个 $G_t$ 是由 MC 采样整个序列得到的，那么就得到了 REINFORCE 算法：

带基线的 REINFORCE

唯一的区别：TD target 从 $G_t$ 变成 $G_t?\hat{v}(S_t,\mathbf{w})$，并且多一个价值网络，也进行跟更新。
好处：

1. 减小方差
2. 加快收敛速度

基线的直觉：
把 TD target 从全为正变成有正有负，更新的时候更有区分度。

Actor-Critic

再把 TD target 变化一下，从多步（MC）变成单步（TD），其他和 REINFORCE 一样。
之所以叫做 Actor-Critic 就是把基线 $\hat{v}(S,\mathbf{w})$ 当作评论家，它评价状态的好坏；而 $\pi (A|S)$ 当作演员，尝试去按照评论家的喜好（体现为 TD target 用评论家来进行估计）来做动作。

总结

REINFORCE：MC，更新慢
$$\delta =G_t$$
$${\theta }_{t+1}\leftarrow {\theta }_t+\alpha \delta ?\ln \pi (A_t|S_t)$$
基线 REINFORCE：MC，更新慢，但是有基线，方差较小，收敛快，调参难度大一些
$$\delta =G_t?\hat{v}(S_t,\mathbf{w})$$
$${\mathbf{w}}_{t+1}\leftarrow {\mathbf{w}}_t+{\alpha }_{\mathbf{w}}\delta ?\hat{v}(S_t)$$
$${\theta }_{t+1}\leftarrow {\theta }_t+{\alpha }_{\theta }\delta ?\ln \pi (A_t|S_t)$$
Actor-Critic：TD，更新快，调参难度大一些
$$\delta =R_t+\gamma \hat{v}(S_t^{\prime },\mathbf{w})?\hat{v}(S_t,\mathbf{w})$$
$${\mathbf{w}}_{t+1}\leftarrow {\mathbf{w}}_t+{\alpha }_{\mathbf{w}}\delta ?\hat{v}(S_t)$$
$${\theta }_{t+1}\leftarrow {\theta }_t+{\alpha }_{\theta }\delta ?\ln \pi (A_t|S_t)$$