【优先级队列 之 堆的实现】

---

前言

---

优先级队列 PriorityQueue

概念：对列是先进先出的的数据结构，但有些情况，数据可能带有优先级，一般出队列时，可能需要优先级高的元素先出队列。所以像这种情况用队列不太合适：在手机上玩游戏时，如果有来电，系统应该优先处理打进来的电话。以前是来电显示充满整个画面，现在变成了一个小窗。

优先队列的模拟实现

PriorityQueue的底层使用了堆这种数据结构（PriorityQueue底层实现是一个完全二叉树，完全二叉树又分为大根堆和小根堆）

堆

概念：
小根堆：根节点比左右孩子都小。只考虑根和左右节点的关系，不考虑左右节点的哪个大。
大根堆：根节点比左右孩子都大

堆的储存方式

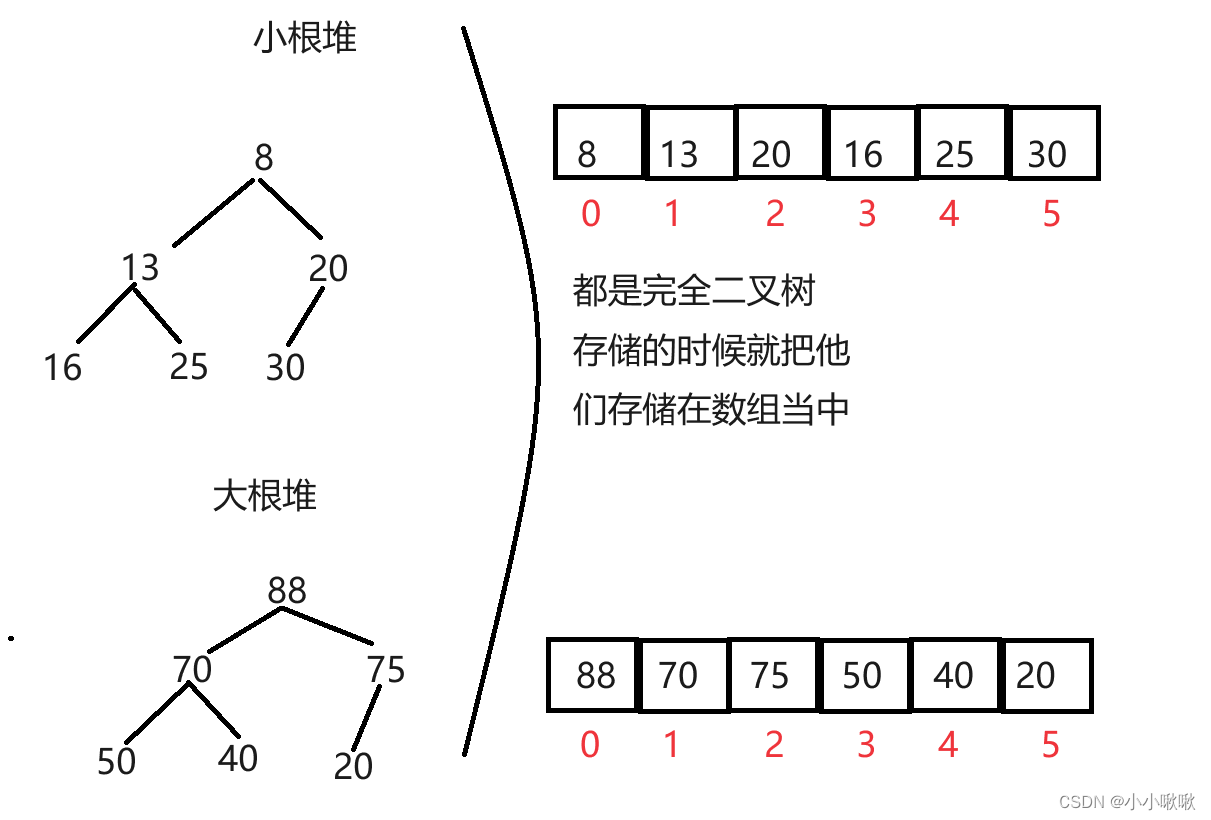
将元素存储到数组中后，可以根据二叉树章节的性质5对树进行还原。假设为节点在数组中的下标，则有: 如果为0，则表示的节点为根节点，否则节点的双亲节点为(i 1)/2
●如果2i+ 1小于节点个数，则节点的左孩子下标为2 门中1,否则没有左孩了
●如果2i+2小于节点个数，则节点的右孩子下标为21+ 2,否则没有右孩子

堆的创建

1. 让parent标记需要调整的节点，child标记parent的左孩子(注意: parent如果有孩子一 定先是有左孩子)
2. 如果parent的左孩子存在，即:child < size,进行以下操作， 直到parent的左孩子不存在
   parent右孩子是否存在，存在找到左右孩子中最大的孩子，让child进行标记
3. 将parent 与较大的孩子child比较,如果:
   parent小于较大的孩子child,交换parent与较大的孩子child,交换完成之后，parent中小的元素向下移动，并继续向下调整，即parent = child; child = parent*2+1;然后继续
   否则:退出循环。

public class TestHeap {
    //创建一个数组
    public int[] elem;
    public int useSize;//有效元素

    //构造方法给elem分配内存
    public TestHeap() {
        this.elem = new int[10];
    }

    //初始化elem数组，给elem传入元素
    public void initElem(int[] array){
        for (int i = 0; i < array.length; i++) {
            elem[i] = array[i];
            useSize++;
        }
    }

    /**
     * 创建大根堆的代码
     */
    public void createHeap(){
        for (int parent =(useSize-1-1)/2 ; parent >=0 ; parent--) {
            siftDown(parent,useSize);

        }
    }

    /**
     * 向下调整
     * @param parent
     * @param len
     */
     //让child标记根的左孩子，如果左孩子大于数组长度则进行下面操作
    // 如果右孩子小于长度并且左孩子的值小于右孩子的值，让左孩子移到右孩子上
    private void siftDown(int parent,int len){
        int child = 2*parent+1;
        while(child < len){
            if (child+1 < len && elem[child] < elem[child+1]){
                child = child+1;
            }
            //此时child保存的是孩子节点中最大的值
            //如果左孩子大于根节点，两者的值交换。
            if (elem[child] > elem[parent]) {
                //和根节点交换
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                //交换完再换位置
                parent = child;//根节点移到孩子节点上
                child = 2*parent+1;//孩子节点再往下移

            }else{
                break;
            }


        }
    }
}

public class Test {
    public static void main(String[] args) {
        TestHeap testHeap = new TestHeap();
        int[] array={27,15,19,18,28,34,65,49,25,37};
        testHeap.initElem(array);
        testHeap.createHeap();
        System.out.println("========");
    }
}

建堆的时间复杂度

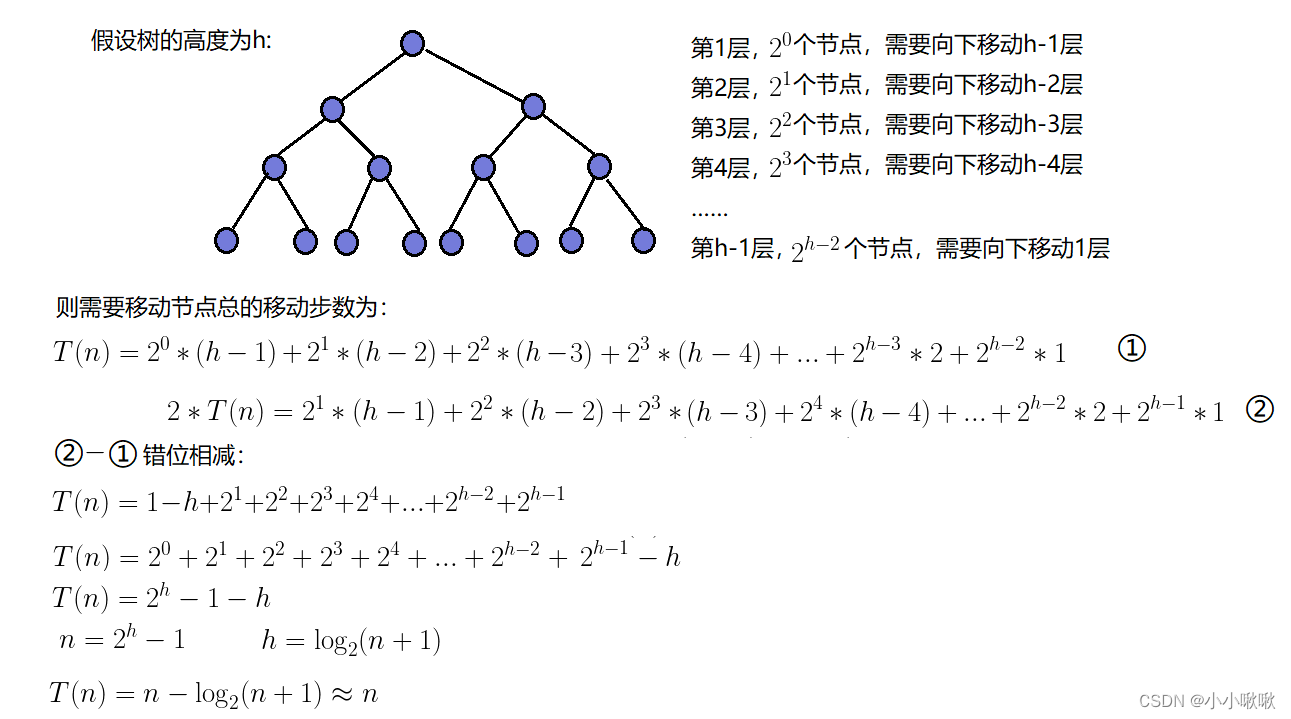
因此：建堆的时间复杂度是0（N）

堆的插入与删除

堆的插入：

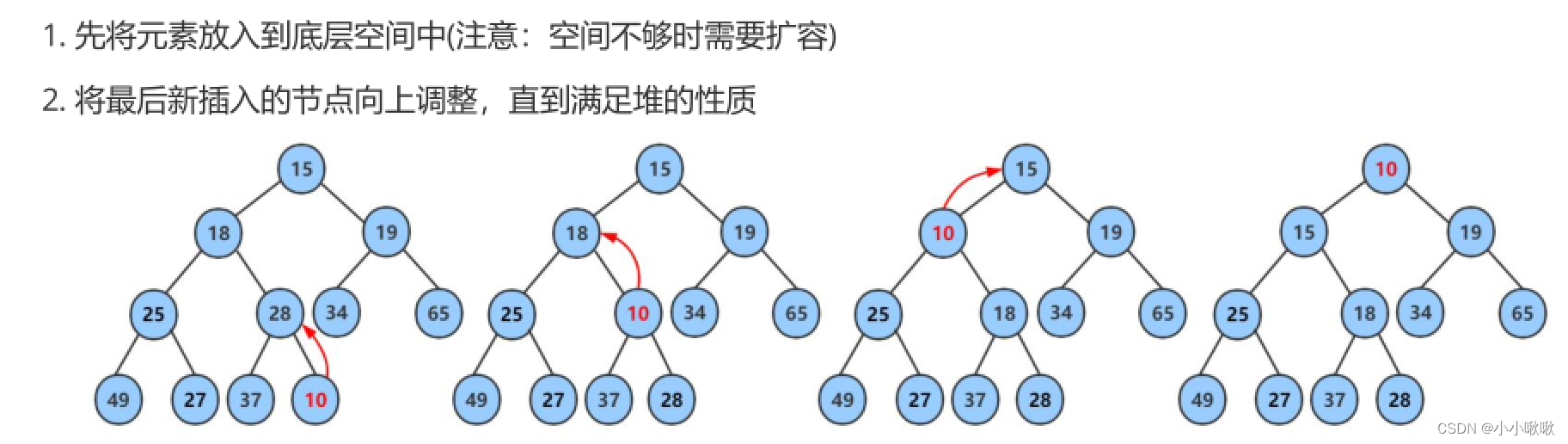
    private void swap(int i,int j){
        int tmp = elem[i];
        elem[i] = elem[j];
        elem[j] = tmp;
    }

    //向上调整
    public void push(int val){
        if(isFull()){
            elem = Arrays.copyOf(elem,elem.length*2);
        }
        elem[usedSize] = val;
        siftUp(usedSize);
        usedSize++;
    }
    public boolean isFull(){
        return usedSize == elem.length;
    }
    public void siftUp(int child){
        int parent = (child-1)/2;
        while(child > 0){
            if (elem[child] > parent){
                swap(child,parent);
                child = parent;
                parent = (child-1)/2;
            }else{
                break;
            }
        }
    }

堆的删除
注意：这里的删除指的是删除堆顶的元素

1. 将0下标的的堆顶元素和堆的最后一个元素交换
2. 将堆的有效个数usedSize–
3. 对堆进行向下调整

    //删除堆顶元素
    public int pop(){
        if (empty()){
            return -1;
        }
        int oldVal = elem[0];
        swap(0,usedSize-1);
        usedSize--;
        siftDown(0,usedSize);
        return oldVal;
    }
    public boolean empty(){
        return usedSize == 0;
    }

总结

本章节学习如何实现一个堆，如何运用到向上调整，向下调整。