1.15 递归

目录

1.两数相加

2.两两交换链表中的节点

3.pow(x,?n)

4.消除游戏

?5.字符串解码

---

1.两数相加

给你两个?非空?的链表，表示两个非负的整数。它们每位数字都是按照?逆序?的方式存储的，并且每个节点只能存储?一位?数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0?开头。

示例 1：

输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

提示：

• 每个链表中的节点数在范围?[1, 100]?内
• 0 <= Node.val <= 9
• 题目数据保证列表表示的数字不含前导零

分析：思路很好想，但是写起来超级麻烦，写了好久，可以细品一下

#include <bits/stdc++.h>

using namespace std;

typedef struct node
{
    int data;
    struct node *next;
};


main()
{
    node *head1=new node;
    node *head2=new node;
    node *head3=new node;
    int x,len1=0,len2=0;
    node *q=new node;
    q=head1;
    cin>>x;
    if(x==0)
    {
        node *p=new node;
        p->data=x;
        q->next=p;
        p->next=NULL;
        q=q->next;
        len1++;
    }
    else
    {
        while(x)
        {
            node *p=new node;
            p->data=x;
            q->next=p;
            p->next=NULL;
            q=q->next;
            len1++;
            cin>>x;

        }
    }

//    q=head1->next;
//    while(q)
//    {
//        cout<<q->data<<" ";
//        q=q->next;
//    }
    q=head2;
    cin>>x;
    if(x==0)
    {
        node *p=new node;
        p->data=x;
        q->next=p;
        p->next=NULL;
        q=q->next;
        len2++;
    }
    else
    {
        while(x)
        {
            node *p=new node;
            p->data=x;
            q->next=p;
            p->next=NULL;
            q=q->next;
            len2++;
            cin>>x;

        }
    }
    cout<<"##################"<<endl;
    cout<<len1<<" "<<len2<<endl;

//    q=head2->next;
//    while(q)
//    {
//        cout<<q->data<<" ";
//        q=q->next;
//    }
     if(len1>len2)
    {
        q=head2;
        while(q->next)
        {
            q=q->next;
//            cout<<q->data<<" ";


        }

        while(len1>len2)
        {

            node *p=new node;
            p->data=0;
            q->next=p;
            p->next=NULL;
            q=q->next;
            len2++;
        }

    }
    if(len1<len2)
    {

        q=head1;
        while(q->next)
        {
            q=q->next;
//            cout<<q->data<<" ";


        }

        while(len1<len2)
        {

            node *p=new node;
            p->data=0;
            q->next=p;
            p->next=NULL;
            q=q->next;
            len1++;
        }
    }
//    cout<<"=========="<<endl;
    int carry=0;
    node *p=new node;
    node *a=new node;
    node *r=new node;
    p=head1->next;
    q=head2->next;
    a=head3;
//    cout<<p<<" "<<q<<endl;
    while(q)
    {
//       cout<<"---------"<<endl;
        node *r=new node;
        a->next=r;
        r->next=NULL;
        x=p->data+q->data+carry;
//       cout<<p->data<<" "<<q->data<<" "<<carry<<" "<<x<<endl;
        r->data=x%10;
        carry=x/10;
        p=p->next;
        q=q->next;
        a=a->next;
        cout<<r->data<<" "<<endl;
    }
    if(carry==1) cout<<carry;






}

2.两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：

输入：head = []
输出：[]

示例 3：

输入：head = [1]
输出：[1]

提示：

• 链表中节点的数目在范围?[0, 100]?内
• 0 <= Node.val <= 100

分析：第一次想到的是可以给一个标记，后来发现根本用不上，只要一次后移两个节点，再单独处理空和只剩一个节点的情况即可

#include <bits/stdc++.h>

using namespace std;

typedef struct node
{
    int data;
    struct node *next;
};

main()
{
    int x;
    node *head=new node;
    head->next=NULL;
    node *q=new node;
    q=head;
    while(cin>>x)
    {
        node *p=new node;
        p->data=x;
        q->next=p;
        p->next=NULL;
        q=q->next;
    }
//    q=head->next;
//    while(q)
//    {
//        cout<<q->data<<" ";
//        q=q->next;
//    }
//    cout<<"##################"<<endl;
    node *p=new node;
    p=head->next;
    if(p) q=p->next;
    while(p&&q)
    {
//        cout<<p->data<<" "<<q->data<<endl;
        swap(p->data,q->data);
//        cout<<p->data<<" "<<q->data<<endl;
        p=q->next;
        if(p) q=p->next;
    }
 //   cout<<"##################";
    q=head->next;
    while(q)
    {
        cout<<q->data<<" ";
        q=q->next;
    }



}

后来发现是必须是交换节点不能直接交换节点里的数据，然后又去分析了一下

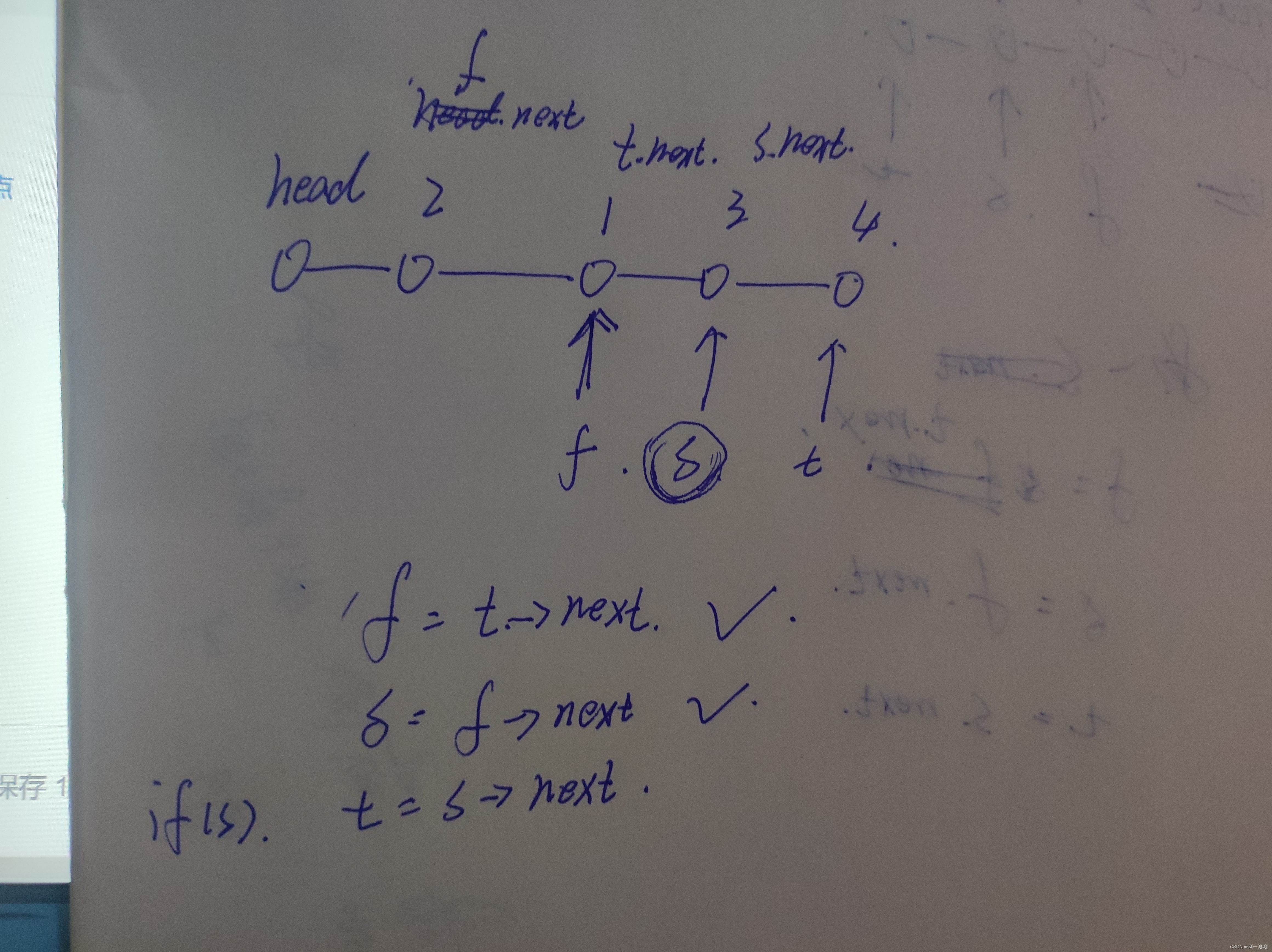
#include <bits/stdc++.h>

using namespace std;

typedef struct node
{
    int data;
    struct node *next;
};

main()
{
    int x;
    node *head=new node;
    head->next=NULL;
    node *q=new node;
    q=head;
    while(cin>>x)
    {
        node *p=new node;
        p->data=x;
        q->next=p;
        p->next=NULL;
        q=q->next;
    }
//    q=head->next;
//    while(q)
//    {
//        cout<<q->data<<" ";
//        q=q->next;
//    }
//    cout<<"##################"<<endl;
    node *f=new node;
    node *s=new node;
    node *t=new node;
    f=head;
    s=f->next;
    if(s) t=s->next;
    while(s&&t)
    {
//        cout<<p->data<<" "<<q->data<<endl;

          f->next=t;
          s->next=t->next;
          t->next=s;

//        cout<<p->data<<" "<<q->data<<endl;
         f=t->next;
         s=f->next;
         if(s) t=s->next;

    }
 //   cout<<"##################";
    q=head->next;
    while(q)
    {
        cout<<q->data<<" ";
        q=q->next;
    }



}

3.pow(x,?n)

实现?pow(x,?n)?，即计算?x?的整数?n?次幂函数（即，xn?）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

• -100.0 < x < 100.0
• -231 <= n <= 231-1
• n?是一个整数
• 要么?x?不为零，要么?n > 0?。
• -104 <= xn <= 104

分析：之前写过一个求幂取余的方法，但是没用递归，打算再试一下

#include <bits/stdc++.h>

using namespace std;

double mypow(double a,int b)
{
    double half,rest;
    if(b==0) return 1;
    if(b==1) return a;
    if(b==-1) return 1/a;
    half=mypow(a,b/2);
    if(b%2==0) rest=1;
    else rest=a;
    return half*half*rest;
}

main()
{
    double a;
    int b;
    cin>>a>>b;
    //printf("%.6f",mypow(a,b));
    cout<<fixed<<setprecision(6)<<mypow(a,b);
}

4.消除游戏

列表?arr?由在范围?[1, n]?中的所有整数组成，并按严格递增排序。请你对?arr?应用下述算法：

• 从左到右，删除第一个数字，然后每隔一个数字删除一个，直到到达列表末尾。
• 重复上面的步骤，但这次是从右到左。也就是，删除最右侧的数字，然后剩下的数字每隔一个删除一个。
• 不断重复这两步，从左到右和从右到左交替进行，直到只剩下一个数字。

给你整数?n?，返回?arr?最后剩下的数字。

示例 1：

输入：n = 9
输出：6
解释：
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9]
arr = [2, 4, 6, 8]
arr = [2, 6]
arr = [6]

示例 2：

输入：n = 1
输出：1

提示：

• 1 <= n <= 109

分析：刚开始想到的是很像约瑟夫环，后来发现行不通，原因是这个题是从第一个数开始删除的，但是约瑟夫环不是，就得重新想办法了

分析：模仿约瑟夫环，我们只需要知道最后留下来的是几就好，从左往右删时，头部肯定需要换掉的，从右往左删时，如果剩余的总数是偶数，那么头部就不需要换，如果是奇数，那就需要换掉，换成它本身加上步长，所以要定义的变量就有总数num，步长step和头部head

#include <bits/stdc++.h>

using namespace std;
int num;

int ys(bool left,int n,int step,int head)
{
    cout<<head<<" "<<step<<" "<<n<<endl;
    if(n==1) return head;
    if(left || n%2==1)
    {
        head=head+step;
    }
    n=n>>1;
    step=step<<1;
    left=!left;
    return ys(left,n,step,head);

}

main()
{
    int step=1,head=1;
    bool left=true;
    cin>>num;
    cout<<ys(left,num,step,head);

}

5.字符串解码

给定一个经过编码的字符串，返回它解码后的字符串。

编码规则为:?k[encoded_string]，表示其中方括号内部的?encoded_string?正好重复?k?次。注意?k?保证为正整数。

你可以认为输入字符串总是有效的；输入字符串中没有额外的空格，且输入的方括号总是符合格式要求的。

此外，你可以认为原始数据不包含数字，所有的数字只表示重复的次数?k?，例如不会出现像?3a?或?2[4]?的输入。

示例 1：

输入：s = "3[a]2[bc]"
输出："aaabcbc"

示例 2：

输入：s = "3[a2[c]]"
输出："accaccacc"

示例 3：

输入：s = "2[abc]3[cd]ef"
输出："abcabccdcdcdef"

示例 4：

输入：s = "abc3[cd]xyz"
输出："abccdcdcdxyz"

提示：

• 1 <= s.length <= 30
• s?由小写英文字母、数字和方括号?'[]'?组成
• s?保证是一个?有效?的输入。
• s?中所有整数的取值范围为?[1, 300]?

?分析：字符串解码很明显是要用栈来写的，很想不通为什么这个题要用递归写，也不知道该怎么用递归来写，在网上看了下他们的递归，是在s[i]为‘['时递归，直到s[i]为']'时返回res

在网上看了下他们的递归. - 力扣（LeetCode）? ? ? ? ??

?在这里它用了一个istringstream iss(s);搜了一下确实有点看不懂，明天要找时间看一下了

#include <bits/stdc++.h>

using namespace std;


main()
{
    int x,i;
    string s;
    getline(cin,s);
    stack<int> k;
    stack<string> ch;
    int multi=0;
    string res="";
    for(i=0; i<s.size(); i++)
    {
        if(s[i]>='0'&&s[i]<='9')
            multi=multi*10+s[i]-'0';
        else if(s[i]=='[')
        {
            k.push(multi);
            ch.push(res);
            multi=0;
            res="";
        }
        else if(s[i]==']')
        {
            string tmp=res;
            for(int j=0; j<k.top()-1; j++)
            {
                tmp+=res;
            }
            res=ch.top()+tmp;
            k.pop();
            ch.pop();


        }
        else
        {
            res=res+s[i];
        }
    }
    cout<<res<<endl;


}