色标在matplotlib和plottable中

是这样的，我有一个数组[-4.4, -2.8, -2.6, -2.2, -1.1, 1.1, 1.2, 1.3, 3.6, 6.0, 6.4, 12.3]，它需要绘制散点图，点的颜色来代表数值大小；同时，也需要在plottable上作为一列显示，同样用颜色来代表数值的大小。
还有两个额外的需求：一、不同的数值的颜色要有区分度；二、0值需要是白色，正值为暖色系，负值为冷色系，从视觉上明显区分正负值。

一、matplotlib色标的选择

matplotlib官方提供了非常多的色标可供选择，可见网址。

按照我的需求，我选择了Diverging colormaps中的PiYG。

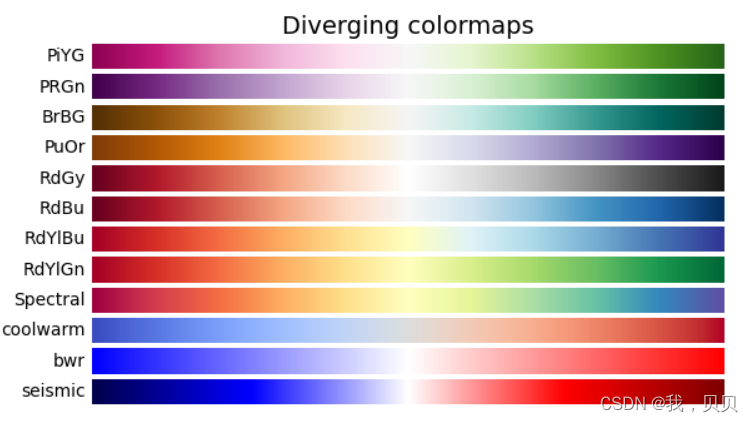
把色标反过来，只需要加 _r。用如下代码查看色标及反过来的色标。

import matplotlib.pyplot as plt
import numpy as np
gradient = np.linspace(0, 1, 256)
gradient = np.vstack((gradient, gradient))
plt.imshow(gradient, aspect='auto', cmap='PiYG')
plt.show()
plt.imshow(gradient, aspect='auto', cmap='PiYG_r')
plt.show()

结果如下

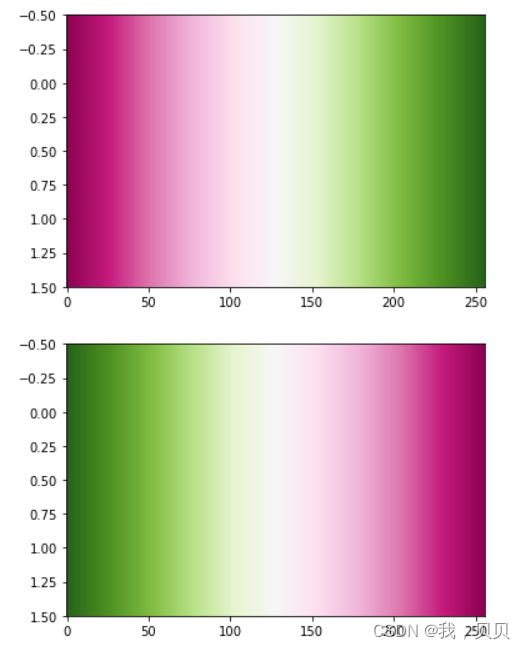
二、画散点图

1、直接画图

import matplotlib
y = [-4.4, -2.8, -2.6, -2.2, -1.1, 1.1, 1.2, 1.3, 3.6, 6.0, 6.4, 12.3]
x = list(range(len(y)))
plt.scatter(x,y,c=y,cmap = matplotlib.cm.PiYG_r) #绘图
cbar = plt.colorbar()   #添加色标
cbar.set_label('Value')   #添加标签
plt.show()   #显示

结果为

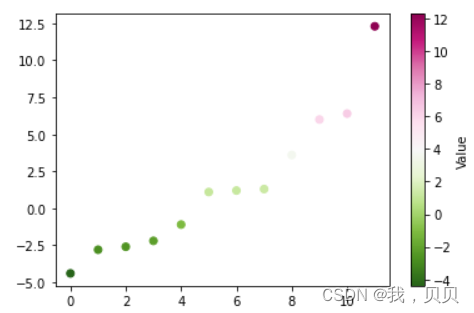
可以看到白色的大概在4左右。

2、添加norm参数

matplotlib.colors模块提供了多种归一化（Normalization）的方式，在官网搜索结果如下：

下面简单介绍一些常用的：

1. Normalize：基本的线性归一化类，将数据线性映射到指定范围内。

2. LogNorm：对数归一化类，将数据进行对数变换后进行线性归一化。

3. PowerNorm：幂归一化类，将数据进行幂变换后进行线性归一化。

4. SymLogNorm：对称对数归一化类，将数据进行对称对数变换后进行线性归一化。

5. BoundaryNorm：边界归一化类，可以将数据映射到离散的颜色值上。

6. TwoSlopeNorm：双斜率归一化类，将数据根据两个斜率进行分段线性归一化。
   通过查看官网的介绍和例子，发现CenteredNorm和TwoSlopeNorm比较符合我的要求。
   尝试如下：

import matplotlib
from matplotlib.colors import TwoSlopeNorm,CenteredNorm
y = [-4.4, -2.8, -2.6, -2.2, -1.1, 1.1, 1.2, 1.3, 3.6, 6.0, 6.4, 12.3]
x = list(range(len(y)))
# 数据归一化
norm1 = TwoSlopeNorm(vmin=min(y), vcenter=0, vmax=max(y))
norm2 = CenteredNorm()
#绘图1
plt.scatter(x,y,c=y,cmap = matplotlib.cm.PiYG_r,norm = norm1) #绘图
cbar = plt.colorbar()   #添加色标
cbar.set_label('Value')   #添加标签
plt.show()   #显示
#绘图2
plt.scatter(x,y,c=y,cmap = matplotlib.cm.PiYG_r,norm = norm2) #绘图
cbar = plt.colorbar()   #添加色标
cbar.set_label('Value')   #添加标签
plt.show()   #显示

结果如下：

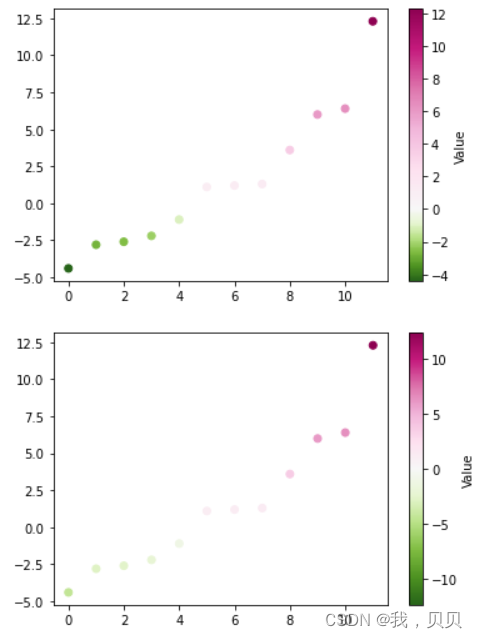
如图可见，两种标准化方法都可以满足0值为白色的要求。但是，TwoSlopeNorm的效果更好，使得负值区的颜色区分更明显。

三、画表格

plottable的官网

1、普通画表格

from plottable import Table
from plottable import ColDef
from plottable.cmap import normed_cmap
from plottable.cmap import centered_cmap
import pandas as pd

#准备数据
tabel_data = pd.DataFrame()
tabel_data['value']=y
#画表
fig,ax = plt.subplots()
Table(
    tabel_data,
    textprops={
        'ha':'center'
    },
    column_definitions=[
        ColDef(name = 'value',textprops={"bbox": {"boxstyle": "circle", "pad": 0.1}}, cmap=matplotlib.cm.PiYG_r),
    ]

).autoset_fontcolors(colnames=["value"])
plt.show()

结果如下：

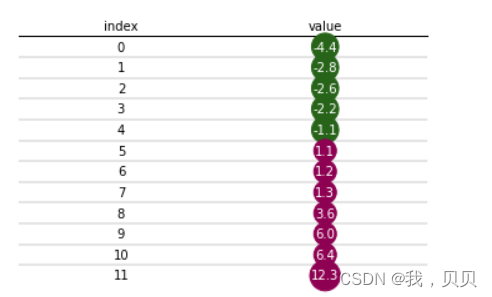
可以区分正负值，但是正值区和负值区里没有颜色深浅来区分值的大小。

2、加参数

以norm为关键词搜索plottable的官方手册，发现它也有标准化方法。但是只有两个。

那么，我可以试一下centered_cmap。

from plottable import Table
from plottable import ColDef
from plottable.cmap import centered_cmap
import pandas as pd

#准备数据
tabel_data = pd.DataFrame()
tabel_data['value']=y
#画表
fig,ax = plt.subplots()
Table(
    tabel_data,
    textprops={
        'ha':'center'
    },
    column_definitions=[
        ColDef(name = 'value',textprops={"bbox": {"boxstyle": "circle", "pad": 0.1}}, cmap=centered_cmap(tabel_data["value"], cmap=matplotlib.cm.PiYG_r)),
    ]

).autoset_fontcolors(colnames=["value"])
plt.show()

结果如下：

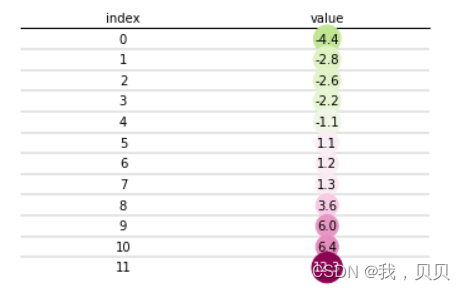
能够按颜色区分正负值。但是和matplotlib的CenteredNorm方法一样，在负值区的颜色区分度不够。

3、增加区分度

在centered_cmap函数中通过num_stds参数调整区分度。当num_stds从默认的2.5调整为1时，结果如下：

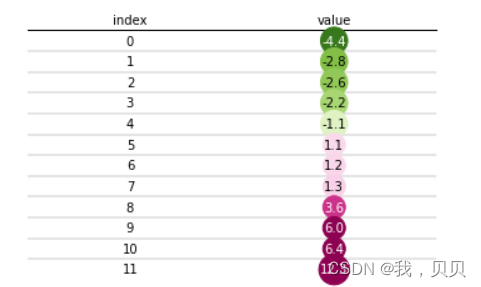
可以发现负值区的区分度增加了，然而正值区的区分度减少了。
归根结底是正值区和负值区的数值离散度不同。
所以，只要正值区和负值区同步调整而不是分别调整，就始终达不到理想的效果。