信道容量与信道编码定理

目录

一. 介绍

二. 信道编码定理

三. 信道编码设计

3.1 码本建设

3.2 编码函数

3.3 译码函数

四. 信道编码错误率

五. 小结

---

一. 介绍

在点对点的通信中，将信源分布表示为：

如果信源在空间U上是均匀分布，那么根据信源编码定理（source coding theorem），信源的熵可直接计算为：

此时则无需特别设计信源编码的过程，只需要一一映射就可以了。比如信源符号的长度为k，那么则可以按顺序直接进行编码为m，如下：

假设信道编码后的长度为n，那么信道编码后的速率为k/n，当然考虑非整数的情况下，信道编码的速率计算为：

接下来讨论时，将信道抽象为离散无记忆信道（discrete memoryless channel），如下：

二. 信道编码定理

信源编码定理参看：

【信息论安全】：信源编码定理-CSDN博客

当信道编码后的码字记为X，概率分布为。信道编码定理说明在随机编码下，借助选择引理（selection lemma），当编码后的码字n足够长时，平均错误概率接近于0.只要这种情况成立则说明一定存在一个信道编码符合此性质。

接下来我们要区别两个概念，一个叫信道可达速率，一个叫信道容量。

将离散无记忆的信道DMC记作：

根据信道编码定理（channel coding theorem），该信道容量（capacity）为：

其中I(X;Y)代表发送信号X与接收信号Y之间的互信息。实际信道的传输速率记为R，那么可得：

三. 信道编码设计

接下来介绍如何基于随机编码来设计可达的信道传输速率。

3.1 码本建设

假定X的概率分布为，首先X与Y的互信息肯定为正数，也就是：

I(X;Y)>0

X与Y之间还会有联合分布，我们将联合分布的最小值记为：

再引入一个很小的参数，也就是：

来了方便后续的阐述。令n为正整数，也就是：

信道传输速率肯定为正数，那么可得：

R>0

将信道编码方案记为：

信道编码方案的设计过程又可以被称之为码本建设（codebook construction）。

编码之前叫m，范围为：

编码之后的长度为n，每个地方记为：

由此编码后的概率为，整体写做

以上码本对所有人公开。

3.2 编码函数

将编码函数记为f，输入为m，输出为

3.3 译码函数

将译码函数记为g，输入为。

如果发现译码之后的信号为，满足：

则说明此时的是正确的。否则译码错误则输出“？”。

四. 信道编码错误率

我们比较关心信道编码中的译码错误概率。所以首先可得：

第一个等号：在已知码本的情况下，研究译码出的与编码前的M不等的概率，并计算其均值；

第二个等号：统计所有不等的概率，所以为求和。并引入m的概率分布。

根据随机编码的对称性，以上概率与m的具体取值无关，由此假设消息m=1，可得：

将译码错误的事件集合在一起，也就是：

理解：也就是对于同一个Y，译码成m的可能性有种，只有一种是正确的，其他全是译码错误的情况，所以可得：

此处是根据联合界引理（union bound），其中的“c”代表补集，也就是非典型集的情况，其概率是很小的，也就是：

从信道传世，它跟其他的肯定是互相独立的，是信道的输出，所以可得：

与是互相独立的：

另外的一个事件其概率上限可计算为：

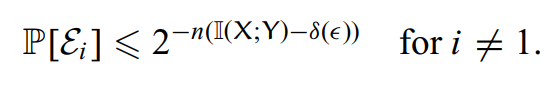
综上将这两个概率相加，可得：

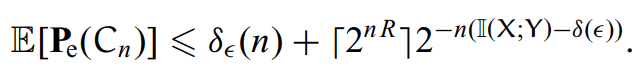
我们需要选择合适的信道传输速率，来保证此解码错误率较低，比如当速率选择：

由此错误率可得：

将码字看成随机变量，错误率看成函数，根据选择引理，一定存在一个码字使其满足：

注意以上求均值的符号“E”去掉了。

在以上讨论过程当中，可以任意小，概率可以随意选择，由此我们得出结论，所有的可达速率需要满足：

五. 小结

在设计数字通信系统时，首先应合理地选择调制解调方法、合适的发射功率等，若仍不能满足系统误码率要求，则要考虑采用差错控制编码措施。

纠错码，是当消息经过有噪信道传输或要恢复存储的数据时用来纠错的。用来传输消息的物理介质叫做信道（如电话线、卫星连接、用于移动通信的无线信道等）。因为纠错码试图克服信道中噪声造成的损害，因此其编码过程又称为信道编码，它常应用于网络安全等领域。

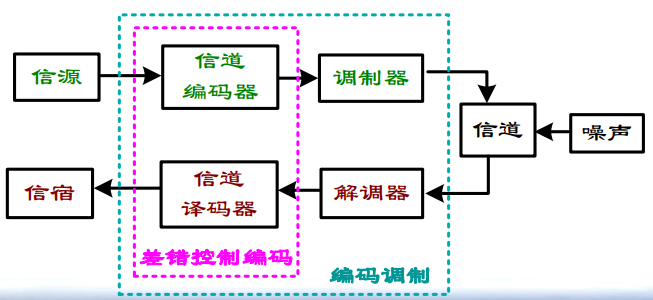
信道编码可分为两个研究领域：波形编码（信号设计）和结构化序列（结构冗余）。波形编码是将波形转变为“更好的波形”以减少错误判决；结构化序列是将数据序列转变为“更好的序列”，通过冗余比特来检测和纠正传输中的错误。

波形编码：最常见的是正交编码和双正交编码，通过编码使编码集合中信号间的相关度最小（即信号间的距离最大）。如对极信号、正交信号。正交编码常使用Hadamard矩阵，即1bit数据集可用两个数字的正交码字进行变换，2bit数据集可使用4个数字的正交码字进行变换，依此类推。

1948年，Bell实验室的C.E.Shannon发表的《通信的数学理论》，是关于现代信息理论的奠基性论文，它的发表标志着信息与编码理论这一学科的创立。Shannon在该文中指出，任何一个通信信道都有确定的信道容量C，如果通信系统所要求的传输速率R小于C，则存在一种编码方法，当码长 n 充分大并应用最大似然译码 （ MLD ， Maximum LikelihoodDecoding）时，信息的错误概率可以达到任意小。从Shannon信道编码定理可知，随着分组码的码长n或卷积码的约束长度N的增加，系统可以取得更好的性能（即更大的保护能力或编码增益），而译码的最优算法是MLD，MLD算法的复杂性随n或N的增加呈指数增加，因此当n或N较大时，MLD在物理上是不可实现的。因此，构造物理可实现编码方案及寻找有效译码算法一直是信道编码理论与技术研究的中心任务。?Shannon指出了可以通过差错控制码在信息传输速率不大于信道容量的前提下实现可靠通信，但却没有给出具体实现差错控制编码的方法.