python数字图像处理基础（十一）——光流估计

概念

光流是空间运动物体在观测成像平面上的像素运动的“瞬时速度”，根据各个像素点的速度矢量特征，可以对图像进行动态分析，例如目标跟踪。要求如下：

• 亮度恒定：同一点随着时间的变化，其亮度不会发生改变。
• 小运动：随着时间的变化不会引起位置的剧烈变化，只有小运动情况下才能用前后帧之间单位位置变化引起的灰度变化去近似灰度对位置的偏导数。
• 空间一致：一个场景上邻近的点投影到图像上也是邻近点，且邻近点速度一致。因为光流法基本方程约束只有一个，而要求x，y方向的速度，有两个未知变量。所以需要连立n多个方程求解。

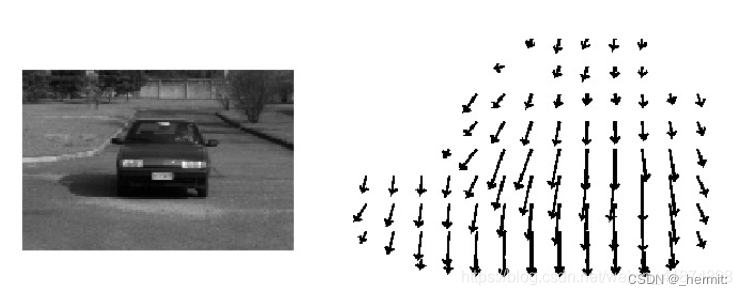
光流估计是计算图像序列中相邻帧之间的像素运动的过程。它旨在通过分析图像中像素强度的变化，推测场景中物体的运动情况。光流估计可以用于许多计算机视觉应用，如视频稳定、目标跟踪、行为分析等。

在光流估计中，通常假设相邻帧之间的像素强度在空间上是连续变化的。这意味着同一场景中的相邻像素之间存在一定的空间连续性，它们通常随着时间的推移而移动。光流估计的目标是找到一个场景中每个像素点的运动向量，表示它在图像中的位移。

有许多不同的光流估计算法，其中一些常见的包括：

1. Lucas-Kanade方法： 这是一个基于局部区域的光流估计方法。它假设一个小的图像块内的像素强度变化是线性的，并通过解一个最小二乘问题来计算局部运动。

2. Horn-Schunck方法： 这是一个全局的光流估计方法，它试图平滑整个场景的光流。该方法在整个图像上定义了一个全局光流场，以最小化场景中所有像素的强度梯度。

3. Farneb?ck方法： 该方法使用多项式来建模局部像素强度变化，并通过计算极小值来估计光流。

4. DeepFlow： 这是一种深度学习方法，使用卷积神经网络来学习复杂的非线性光流。

光流估计在计算机视觉领域中有着广泛的应用，特别是在视频处理和分析中。通过了解图像序列中物体的运动，我们可以更好地理解场景的动态变化，从而支持许多应用，如行为分析、目标跟踪和视频稳定。

Lucas-Kanade算法

Lucas-Kanade算法是一种经典的光流估计方法，用于计算图像序列中相邻帧之间的像素运动。该算法基于以下假设：在局部区域内，像素强度的运动是线性的。具体来说，该算法考虑图像中的每个像素周围的小邻域，并假设该邻域内的像素强度变化可以用一个位移向量来描述。

算法的基本思想如下：

1. 选择一个窗口或局部邻域，通常是一个小的正方形区域。
2. 在该邻域内，假设像素强度在时间上的变化是线性的。
3. 使用最小二乘法，通过拟合一个位移向量来估计像素的运动。

更具体地，考虑两幅相邻的图像帧$I(x,y,t_1)$和$I(x+\Delta x,y+\Delta y,t_2)$，其中$(x,y)$是图像中的坐标，$t_1$和$t_2$是两个不同的时间点。对于局部邻域内的像素，我们可以将其灰度值变化表示为：

$I_x=\frac{?I}{?x},I_y=\frac{?I}{?y},I_t=\frac{?I}{?t}$

其中，$I_x$和$I_y$分别是图像在$x$和$y$方向上的空间梯度，$I_t$是图像在时间上的梯度。

Lucas-Kanade方法通过解决以下线性方程组来估计位移向量$(\Delta x,\Delta y)$：

$$\left[\begin{array}{cc}{I}_x(x_1,y_1)& I_y(x_1,y_1)\\ I_x(x_2,y_2)& I_y(x_2,y_2)\\ ?& ?\\ I_x(x_n,y_n)& I_y(x_n,y_n)\end{array}\right]\left[\begin{array}{c}\Delta x\\ \Delta y\end{array}\right]=?\left[\begin{array}{c}{I}_t(x_1,y_1)\\ I_t(x_2,y_2)\\ ?\\ I_t(x_n,y_n)\end{array}\right]$$

其中，$(x_i,y_i)$表示邻域内的像素坐标，$n$是邻域内像素的数量。通过求解这个线性方程组，可以得到位移向量$(\Delta x,\Delta y)$，从而估计像素的运动。

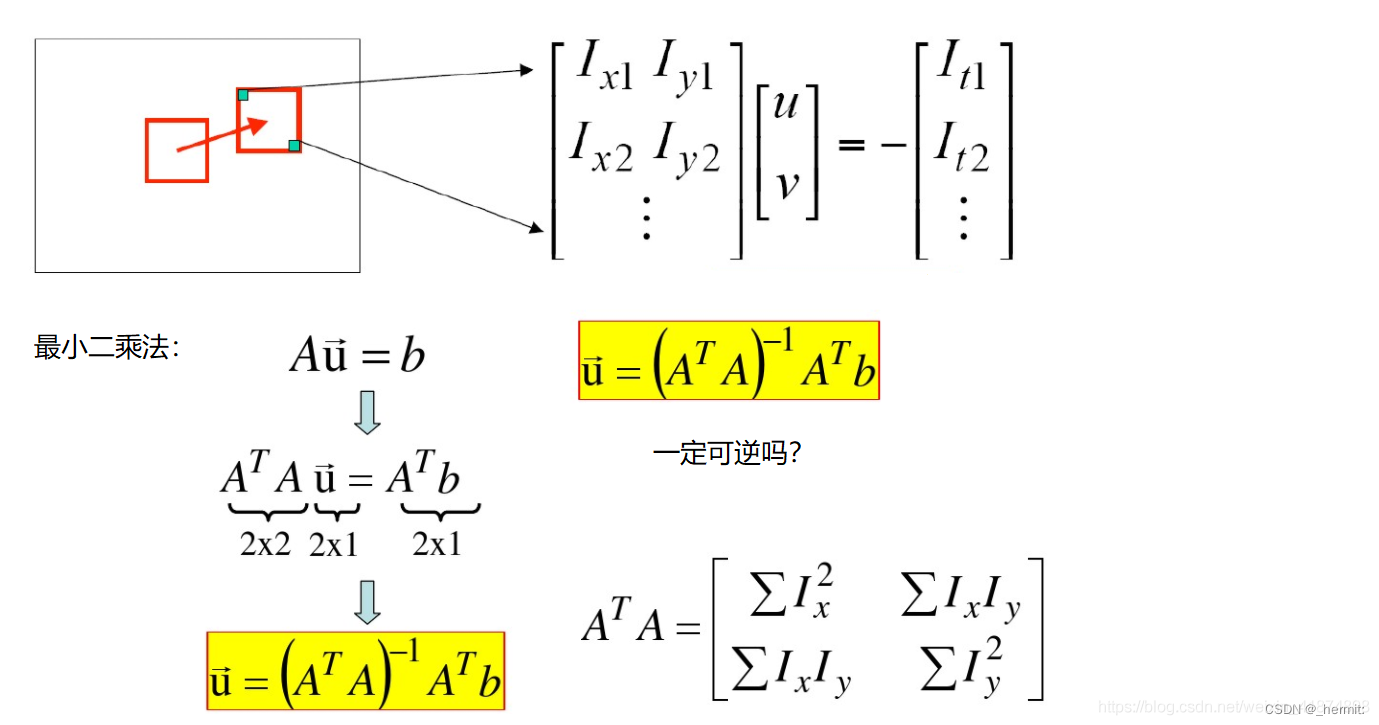
Lucas-Kanade算法的优点在于其计算效率，特别是在局部邻域内像素运动比较均匀的情况下。然而，它对于像素运动比较剧烈或者存在遮挡时可能表现不佳。在实际应用中，Lucas-Kanade算法通常会与金字塔法结合使用，以处理不同尺度上的运动。

• 简单概括为：

泰勒级数展开

类似索贝尔算子sobel

最小二乘法 线性回归方程

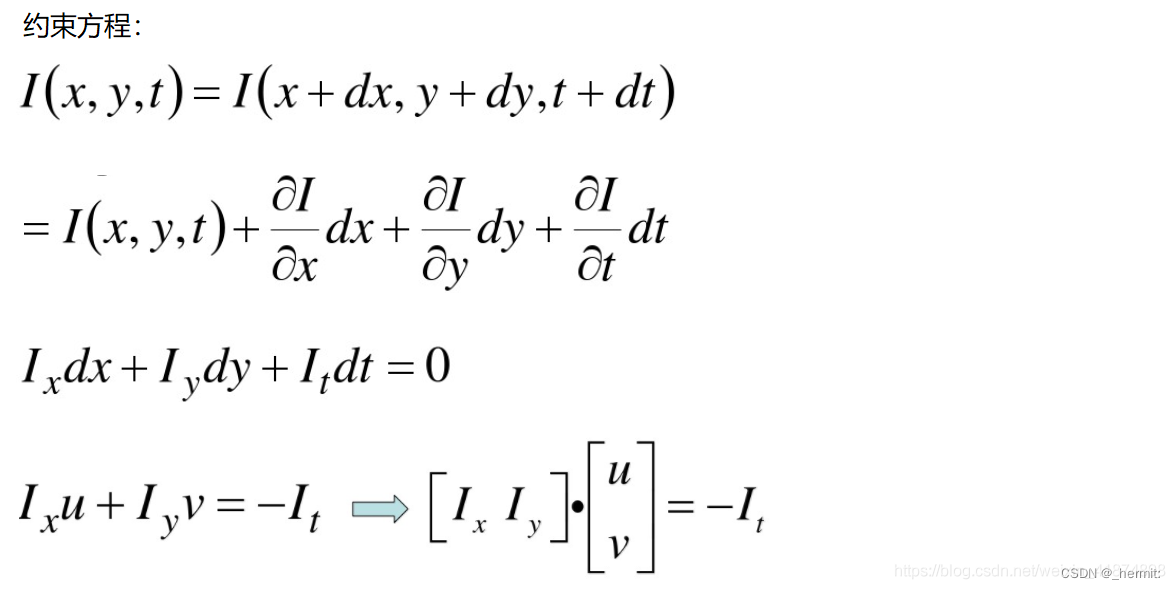
函数表达式

• p0 = cv2.goodFeaturesToTrack(old_gray, mask=None, **feature_params)

作用：用于获得光流估计所需要的角点
参数说明：

• old_gray表示输入图片；
• mask表示掩模；
• feature_params:maxCorners=100角点的最大个数（可以小于该数）,qualityLevel=0.3角点品质,minDistance=7即在这个范围内只存在一个品质最好的角点；

返回值：为(n, 1, 2)的矩阵

• pl, st, err = cv2.calcOpticalFlowPyrLK(old_gray, frame_gray, p0,None, **lk_params)

作用：获得光流检测后的角点位置

参数说明：

• pl表示光流检测后的角点(特征点)位置，输出跟踪角点(特征点)向量；
• st表示是否是运动的角点(特征点)，找到的状态为1，未找到的状态为0；
• err表示是否出错；
• old_gray表示输入前一帧图片；
• frame_gray表示后一帧图片；
• p0表示需要检测的角点，为cv2.goodFeaturesToTrack检测到的角点；
• lk_params：winSize表示选择多少个点进行u和v的求解，即搜索窗口的大小；maxLevel表示空间金字塔的层数

步骤：

角点检测、传入参数

import numpy as np
import cv2

cap = cv2.VideoCapture('./image/test1.mp4')

# 角点检测所需参数
feature_params = dict(maxCorners=100,
                      qualityLevel=0.3,
                      minDistance=7)

# lucas kanade参数
lk_params = dict(winSize=(15, 15),
                 maxLevel=2)  # 窗口大小为15*15，金字塔层数为2

# 随机颜色条
color = np.random.randint(0, 255, (100, 3))

# 拿到第一帧图像
ret, old_frame = cap.read()
old_gray = cv2.cvtColor(old_frame, cv2.COLOR_BGR2GRAY)
# 返回所有检测特征点，需要输入图像，角点最大数量（效率），品质因子（特征值越大的越好，来筛选）
# 距离相当于这区间有比这个角点强的，就不要这个弱的了
p0 = cv2.goodFeaturesToTrack(old_gray, mask=None, **feature_params)  # 寻找角点

# 创建一个mask
mask = np.zeros_like(old_frame)

while True:
    ret, frame = cap.read()  # 这个是取的第二帧图像，上面已经取出了第一帧图像
    frame_gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)

    # 需要传入前一帧和当前图像以及前一帧检测到的角点
    p1, st, err = cv2.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)

    # st=1表示
    good_new = p1[st == 1]
    print(p1.shape)  # (n,1,2)
    print(good_new.shape)  # (n, 2)
    good_old = p0[st == 1]

    # 绘制轨迹
    for i, (new, old) in enumerate(zip(good_new, good_old)):
        # new=[692.99805  83.00432]
        a, b = new.ravel()  # 或者[a, b] = new
        c, d = old.ravel()
        # print(a,b,c,d),检测发现a,b,c,d为浮点数，而cv.circle()函数中的圆心坐标不能是浮点数的类型, 要转换成整数才行，于是就使用int()强制类型转换，之后代码成功运行。
        mask = cv2.line(mask, (int(a), int(b)), (int(c), int(d)), color[i].tolist(), 2)
        # python tolist()方法，将数组或者矩阵转换成列表
        frame = cv2.circle(frame, (int(a), int(b)), 5, color[i].tolist(), -1)

    img = cv2.add(frame, mask)  # 这个相加不会超出边界

    cv2.imshow('frame', img)
    k = cv2.waitKey(150) & 0xff
    if k == 27:
        break

    # 更新
    old_gray = frame_gray.copy()
    p0 = good_new.reshape(-1, 1, 2)

cv2.destroyAllWindows()
cap.release()

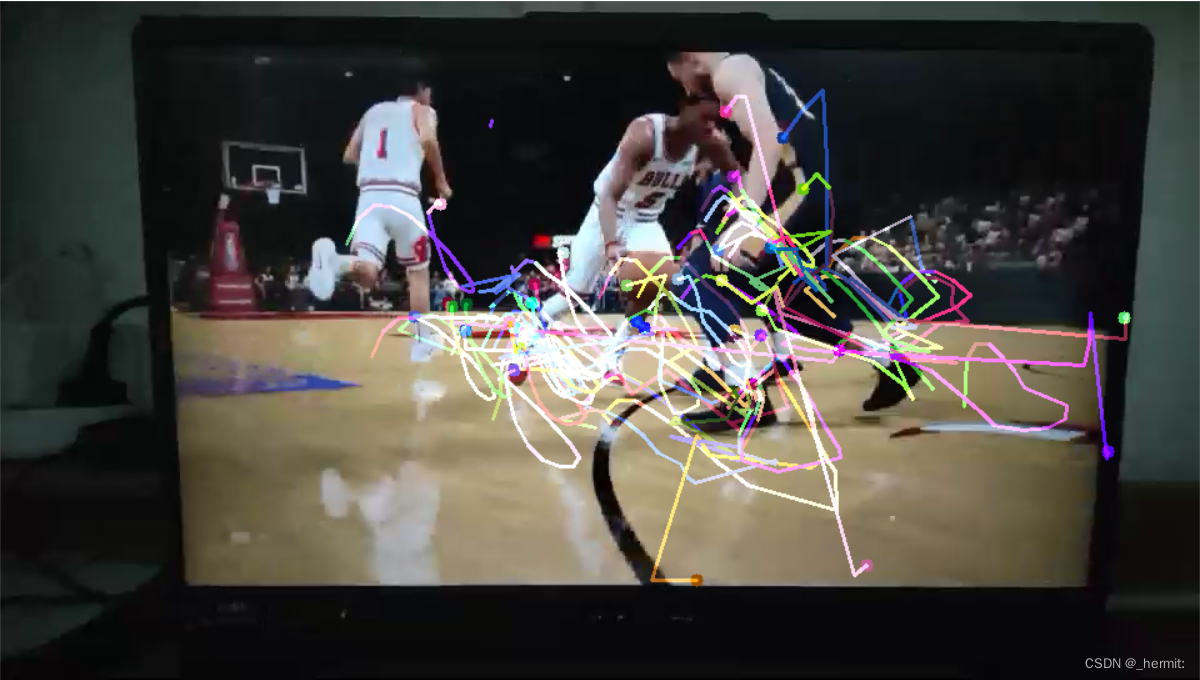
（随便用了一个视频试试效果）