MIT_线性代数笔记：第 27 讲 正定矩阵和最小值

本讲学习正定矩阵，这部分内容将本课程之前的知识点：主元、行列式、特征值以及方程的稳定性融为一体。本讲介绍如何判定一个矩阵是否正定矩阵，以及当一个矩阵是正定矩阵时，其内涵和矩阵操作的效果有何特别之处。此外还有正定矩阵与几何的关系：椭圆和正定有关，双曲线与正定无关。

正定矩阵 Positive definite matrices

给定一个 2×2 矩阵$\left[\begin{array}{cc}a& b\\ b& c\end{array}\right]$ ，有四个途径判定矩阵是否正定矩阵：
1） 特征值：${\lambda }_1>0，{\lambda }_2>0$
2） 行列式（所有子行列式）：a>0，ac-b2>0
3） 主元：a>0，(ac-b2)/a>0
4） 表达式 $x^{T}Ax>0$（x=0 除外）。通常这就是正定的定义，而前三条是用来验证正定性的条件。

给定矩阵 $\left[\begin{array}{cc}2& 6\\ 6& y\end{array}\right]$，从判据可知矩阵为正定阵的条件是 2y-36>0，即 y>18。

矩阵$\left[\begin{array}{cc}2& 6\\ 6& 18\end{array}\right]$正好处在判定为正定矩阵的临界点上，称之为半正定（positive semidefinite）矩阵，它具有一个特征值 0，是奇异矩阵，只有一个主元，行列式为 0。半正定矩阵特征值大于等于 0。

再观察 xTAx 判据：
$$\begin{gathered} x^{T}Ax=\left[\begin{array}{cc}{x}_1& x_2\end{array}\right]\left[\begin{array}{cc}2& 6\\ 6& 18\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right] \\ =2x_1^2+12x_1{x}_2+18x_2^2 \end{gathered}$$
之前讨论得都是线性方程 Ax，现在引入 $x^T$，变成二次，如果对于任意 x，y，这种二次型（quadratic form）$a{x}^2+2bxy+c{y}^2$ 均大于零，则矩阵为正定矩阵。 在本例的半正定矩阵中，当$x1=3$，$x2=?1$时 $2x_1^2+12x_1{x}_2+18x_2^2=2(x_1+3x_2{)}^2=0$。

如果将矩阵变为$\left[\begin{array}{cc}2& 6\\ 6& 7\end{array}\right]$，二次型为$f(x,y)=2x^2+12xy+7y^2$，从几何图像上看没有最小值点，在原点处有一鞍点。鞍点在某个方向上看是极大值点，在另一方向上是极小值点，实际上最佳观测角度是特征向量的方向。

如果将矩阵变为 $\left[\begin{array}{cc}2& 6\\ 6& 20\end{array}\right]$，主元为正；特征值之积为行列式的值 4,和为矩阵的迹 22，因此特征值为正；子行列式均为正。矩阵为正定矩阵。

最小值

二次型$f(x,y)=2x^2+12xy+20y^2$ ，其图像最小值点为原点，一阶偏导数为 0，二阶偏导数为正。

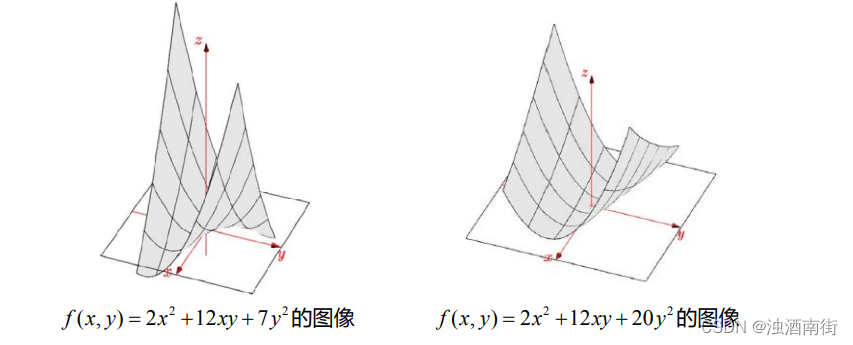
微积分中判定最小值点的判据：一阶导数等于零 $\frac{du}{dx}=0$，二阶导数为正 $\frac{d^{2}u}{d{x}^2}=0$。线性代数中判据为二阶导数矩阵正定。
对于二次型我们可以用配方的办法来验证其是否具有最小值：

$f(x,y)=2x^2+12xy+20y^2=2(x+3y{)}^2+2y^2$

配方使得 $x^2$的系数和交叉项 xy 的系数配合形成完全平方的形式，这个时候用到的 $y^2$的系数正好是 18，即判定正定的临界点。如果实际的系数 d 大于 18，则还剩余(d-18)y2，二次型在原点之外一定大于零，若小于 18 则二次型可以小于等于 0。

对于 $f(x,y)=2x^2+12xy+20y^2=2(x+3y{)}^2+2y^2$，其几何图像为碗型的曲面，如果我们用 f=1 的截面横截曲面，得到的就是$2(x+3y{)}^2+2y^2=1$ 的椭圆曲线。而对于双曲面进行切割就得到双曲线。

配方法其实就是消元：
$\left[\begin{array}{cc}2x^2& 6xy\\ 6xy& 20y^2\end{array}\right],\left[\begin{array}{cc}2& 6\\ 6& 20\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 3& 1\end{array}\right]\left[\begin{array}{cc}2& 6\\ 0& 2\end{array}\right],f(x,y)=2(x+3y{)}^2+2y^2$

主元就是平方项系数，L 矩阵中的行操作数 $l_{21}$就是配方项内 y 的系数。因此这就是为什么主元为正则矩阵为正定矩阵，因为主元是每一个完全平方项的系数。本例中二次型表达式的配方说明了二维的情形，而线代的理论可以将之推广到 n 维。

二阶导数的矩阵记为$\left[\begin{array}{cc}{f}_{xx}& f_{xy}\\ f_{yx}& f_{yy}\end{array}\right]$ ，矩阵对称代表交叉二阶偏导数与求导顺序无关 $f_{xy}=f_{yx}$。在微积分中我们学到的判据 $f_{xx}{f}_{yy}>f_{xy}^2$，和二阶矩阵判定正定是等价的，并且线代可以推广到 n 维。

3 阶矩阵

$A=\left[\begin{array}{ccc}2& ?1& 0\\ ?1& 2& ?1\\ 0& ?1& 2\end{array}\right]$，它是正定矩阵。计算子行列式得到$\left|\begin{array}{c}2\end{array}\right|=2$,$\left|\begin{array}{cc}2& ?1\\ ?1& 2\end{array}\right|=3$,$\left|\begin{array}{ccc}2& ?1& 0\\ ?1& 2& ?1\\ 0& ?1& 2\end{array}\right|=4$。

主元是 2，3/2，4/3。特征值是 $2?\sqrt{2}$ ，$2$，$2+\sqrt{2}$ 。

这是 GS 最爱的矩阵之一，可以用来把二阶微分方程变成离散问题，因为它每一行都是差分方程$f_{n+1}?2f_n+f_{n?1}$。

其二次型为$x^{T}Ax=2x_1^2+2x_2^2+2x_3^2?2x_1{x}_2?2x_2{x}_3$
这是一个四维的图像，三个维度 x1，x2，x3，还有函数 f，如果用 f=1 切割图像，则得到 $2x_1^2+2x_2^2+2x_3^2?2x_1{x}_2?2x_2{x}_3=1$ 。这是一个椭球体，三个特征值不同，因此椭球的三个长轴长度不同。三个轴的方向就是特征向量的方向，轴长度就是特征值，矩阵的分解 $A=Q\Lambda Q^T$很好的说明了这件事，这就是所谓的“主轴定理”。