Offer必备算法_双指针_八道力扣OJ题详解（由浅到深）
目录
????????Offer必备算法的第一篇，以后以类似的形式更新各种算法原理和刷题，如：双指针，滑动窗口，二分查找，前缀和，位运算，分治，链表，哈希表，栈和队列，BFS和DFS，递归，搜索，回溯，floodfill，斐波那契，动态规划，贪心算法等等。
????????前面C语言和C++的学习我们也用过双指针，下面来系统的学习一下双指针算法。
双指针算法原理
? ? ? ? 双指针算法是一种处理线性结构的有效方法，它利用了两个指针分别位于序列的不同位置，通过它们之间的移动来实现问题的求解或满足特定的条件。这种算法的核心思想是利用指针的移动来逐步缩小待解决问题的规模。双指针算法可以应用于任何包含顺序存储的线性数据结构中，特别是那些可以进行适当并行处理的场景。
具体来说，双指针算法涉及以下步骤：
-
初始化：创建两个指针，一个用于遍历序列的前半部分，另一个用于遍历序列的后半部分。这两个指针通常初始化为序列的起始和末尾位置。
-
移动指针：重复执行以下操作之一，直至找到所需的解决方案或其他终止条件：
- 同时移动两个指针相同的步长；
- 一个指针后移，另一个指针前移相同的步长；
- 两个指针交替前进，使得每次只有一个指针改变其当前位置。
-
停止条件：当两个指针相遇（即到达同一位置），或者达到预设的条件时，算法结束并返回结果。
????????双指针算法的一个关键优势在于它可以充分利用数组的有序性，这可能导致某些计算变得更加简单，从而降低时间复杂度。在一些情况下，双指针算法可以将时间复杂度从O(N^2)降低到O(N)，尤其是当指针的移动是基于数组已排序的信息时。
①力扣283. 移动零
难度 简单
给定一个数组?nums，编写一个函数将所有?0?移动到数组的末尾，同时保持非零元素的相对顺序。
请注意?，必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums =[0,1,0,3,12]输出:[1,3,12,0,0]
示例 2:
输入: nums =[0]输出:[0]
提示:
1 <= nums.length <= 10^4-2^31?<= nums[i] <= 2^31?- 1
进阶：你能尽量减少完成的操作次数吗？
class Solution {
public:
void moveZeroes(vector<int>& nums) {
}
};解析代码
经典的双指针问题（数组的双指针问题就是运用下标模拟指针）
后面的双指针难度慢慢增加，这里直接放代码：
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int letf = 0, right = 0, size = nums.size();
while(right < size)
{
if(nums[right] != 0)
{
swap(nums[letf++], nums[right]);
}
++right;
}
}
};②力扣1089. 复写零
难度 简单
给你一个长度固定的整数数组?arr?，请你将该数组中出现的每个零都复写一遍，并将其余的元素向右平移。
注意：请不要在超过该数组长度的位置写入元素。请对输入的数组?就地?进行上述修改，不要从函数返回任何东西。
示例 1：
输入：arr = [1,0,2,3,0,4,5,0] 输出：[1,0,0,2,3,0,0,4] 解释：调用函数后，输入的数组将被修改为：[1,0,0,2,3,0,0,4]
示例 2：
输入：arr = [1,2,3] 输出：[1,2,3] 解释：调用函数后，输入的数组将被修改为：[1,2,3]
提示：
1 <= arr.length <= 10^40 <= arr[i] <= 9
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
}
};解析代码
从右往前的双指针问题（标的难度是简单实际并不简单），需要先找到最后得到的vector最右边的数。这里找这个数用从左向右的双指针：
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
int left = -1, right = 0, size = arr.size();
while(right < size) // 找到最后一个数
{
if(arr[right] != 0)
{
left++;
}
else
{
left += 2;
}
if(left >= size - 1)
{
break;
}
right++;
}
if(left == size) // 处理边界情况
{
arr[size - 1] = 0;
right --;
left -= 2;
}
while(right >= 0) // 从右往左复写
{
if(arr[right] != 0)
{
arr[left--] = arr[right--];
}
else
{
arr[left--] = 0;
arr[left--] = 0;
right--;
}
}
}
};③力扣202. 快乐数
难度 简单
编写一个算法来判断一个数?n?是不是快乐数。
「快乐数」?定义为：
- 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1，也可能是?无限循环?但始终变不到 1。
- 如果这个过程?结果为?1，那么这个数就是快乐数。
如果?n?是?快乐数?就返回?true?；不是，则返回?false?。
示例 1：
输入：n = 19 输出：true 解释： 12 + 92 = 82 82 + 22 = 68 62 + 82 = 100 12 + 02 + 02 = 1
示例 2：
输入：n = 2 输出：false
提示：
1 <= n <= 23^1 - 1
class Solution {
public:
bool isHappy(int n) {
}
};解析代码
类似判断环形链表的快慢指针，了解一下鸽巢原理：
看一下环形链表的讲解：
数据结构与算法⑥(第二章OJ题，下)后八道链表面试题-CSDN博客
此题为什么一定会成环？：
此题中最大范围为23^1 - 1 等于?2.1*10^9 小于?9999999999（10个9）-> 每个数平方后相加为9^2 * 10 = 810，所以超过810次每个数平方后，至少会有两个数落在[1,810]，此时成环的时候slow等于1就是快乐数。
通过代码：
class Solution {
public:
int bitSum(int n)
{
int sum = 0;
while(n)
{
int x = n % 10;
sum += x*x;
n /= 10;
}
return sum;
}
bool isHappy(int n) {
int slow = n, fast = bitSum(n);
while(slow != fast)
{
slow = bitSum(slow);
fast = bitSum(bitSum(fast));
}
return slow == 1;
}
};④力扣11. 盛最多水的容器
难度 中等
给定一个长度为?n?的整数数组?height?。有?n?条垂线，第?i?条线的两个端点是?(i, 0)?和?(i, height[i])?。
找出其中的两条线，使得它们与?x?轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明：你不能倾斜容器。
示例 1：
?
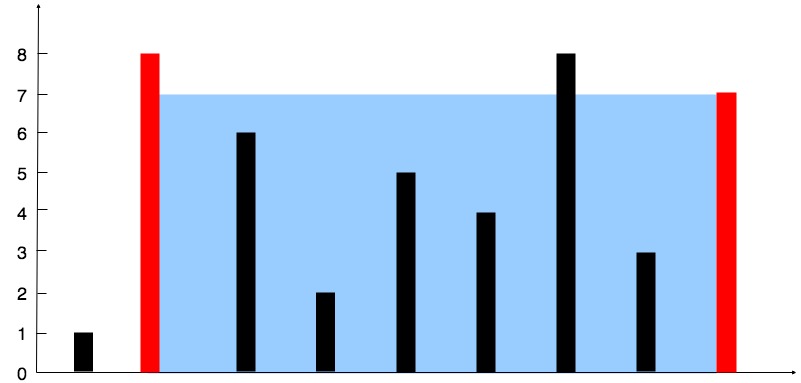输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为?49。
示例 2：
输入：height = [1,1] 输出：1
提示：
n == height.length2 <= n <= 10^50 <= height[i] <= 10^4
class Solution {
public:
int maxArea(vector<int>& height) {
}
};解析代码
首先想到的是两层循环的暴力解法，时间复杂度是O（N^2），这里采用双指针（对撞指针）的思想优化到O（N）：
设两个指针 left ， right 分别指向容器的左右两个端点，此时容器的容积 :
v = （right - left）?* min（height [ right ], height [ left ] ）
容器的左边界为 height [ left ]? ，右边界为 height [ right ] 。
为了方便叙述，假设「左边边界」小于「右边边界」。
- 容器的宽度一定变小。
- 由于左边界较小，决定了水的高度。如果改变左边界，新的水面高度不确定，但是一定不会超过右边的柱子高度，因此容器的容积可能会增大。
- 如果改变右边界,无论右边界移动到哪里，新的水面的高度一定不会超过左边界，也就是不会超过现在的水面高度，但是由于容器的宽度减小，因此容器的容积一定会变小。
由此可见，左边界和其余边界的组合情况都可以舍去。所以可以left++跳过这个边界，继续去判断下一个左右边界。
不断重复上述过程，每次都可以舍去大量不必要的枚举过程，直到left与right相遇。期间产生的所有的容积里面的最大值，就是最终答案。
代码：
class Solution {
public:
int maxArea(vector<int>& height) {
int left = 0, right = height.size() - 1, ret = 0;
while(left < right)
{
int v = (right - left) * min(height[left], height[right]);
ret = max(v, ret);
if(height[left] < height[right]) // 哪个小哪个就往中间移动
{
++left;
}
else
{
--right;
}
}
return ret;
}
};⑤力扣611. 有效三角形的个数
难度 中等
给定一个包含非负整数的数组?nums?，返回其中可以组成三角形三条边的三元组个数。
示例 1:
输入: nums = [2,2,3,4] 输出: 3 解释:有效的组合是: 2,3,4 (使用第一个 2) 2,3,4 (使用第二个 2) 2,2,3
示例 2:
输入: nums = [4,2,3,4] 输出: 4
提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000
class Solution {
public:
int triangleNumber(vector<int>& nums) {
}
};解析代码
暴力法：（这里代码就不写了，时间复杂度是O（N^3））
三层 for 循环枚举出所有的三元组，并且判断是否能构成三角形。
虽然说是暴力求解，但还是可以优化一下：
如果能构成三角形，需要满足任意两边之和要大于第三边。但是实际上只需让较小的两条边之和大于第三边即可。因此我们可以先将原数组排序，然后从小到大枚举三元组，一方面省去枚举的数量，另一方面方便判断是否能构成三角形。
双指针：时间复杂度是O（N^2）
先将数组排序。根据暴力法中的优化思想，我们可以固定一个“最长边”，然后在比这条边小的有序数组中找出一个二元组，使这个二元组之和大于这个最长边。由于数组是有序的，我们可以利用“对撞指针”来优化。
设最长边枚举到 i 位置，区间 [left，right] 是 i 位置左边的区间 （也就是比它小的区间）：如果 nums[left] + nums[right] > nums[i] ，
说明 [left，right - 1] 区间上的所有元素均可以与 nums[right] 构成比nums[i] 大的二元组，
满足条件的有 right - left 种，此时 right 位置的元素的所有情况相当于全部考虑完毕， 减减right?，进入下一轮判断，
如果 nums[left] + nums[right] <= nums[i] ，
说明 left 位置的元素是不可能与 [left + 1，right] 位置上的元素构成满足条件的二元组，此时left 位置的元素可以舍去， 加加left?进入下轮循环。双指针代码：
class Solution {
public:
int triangleNumber(vector<int>& nums) {
sort(nums.begin(), nums.end());
int ret = 0, pos = nums.size() - 1; // 固定的数
for(int i = pos; i >= 2; --i) // 因为至少三个数，所以大于等于2
{
int left = 0, right = i - 1;
while(left < right)
{
if(nums[left] + nums[right] > nums[i])
{
ret += (right - left);
--right;
}
else
{
++left;
}
}
}
return ret;
}
};⑥剑指 Offer 57. 和为s的两个数字
LCR 179. 查找总价格为目标值的两个商品 - 力扣（LeetCode）
难度 简单
购物车内的商品价格按照升序记录于数组?price。请在购物车中找到两个商品的价格总和刚好是?target。若存在多种情况，返回任一结果即可。
示例 1：
输入：price = [3, 9, 12, 15], target = 18 输出：[3,15] 或者 [15,3]
示例 2：
输入：price = [8, 21, 27, 34, 52, 66], target = 61 输出：[27,34] 或者 [34,27]
提示：
1 <= price.length <= 10^51 <= price[i] <= 10^61 <= target <= 2*10^6
class Solution {
public:
vector<int> twoSum(vector<int>& price, int target) {
}
};解析代码：
和上一篇博客即力扣611的思路一样，双指针时间复杂度为O（N）的代码：
class Solution {
public:
vector<int> twoSum(vector<int>& price, int target) {
int left = 0, right = price.size() - 1;
while(left < right)
{
int sum = price[left] + price[right];
if(sum < target)
{
++left;
}
else if(sum > target)
{
--right;
}
else
{
return {price[left], price[right]}; // 直接构造成vector返回
}
}
return {-1,-1}; // 预防编译器的检查
}
};⑦力扣15. 三数之和
难度 中等
给你一个整数数组?nums?，判断是否存在三元组?[nums[i], nums[j], nums[k]]?满足?i != j、i != k?且?j != k?，同时还满足?nums[i] + nums[j] + nums[k] == 0?。请
你返回所有和为?0?且不重复的三元组。
注意：答案中不可以包含重复的三元组。
示例 1：
输入：nums = [-1,0,1,2,-1,-4] 输出：[[-1,-1,2],[-1,0,1]] 解释： nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。 nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。 nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。 注意，输出的顺序和三元组的顺序并不重要。
示例 2：
输入：nums = [0,1,1] 输出：[] 解释：唯一可能的三元组和不为 0 。
示例 3：
输入：nums = [0,0,0] 输出：[[0,0,0]] 解释：唯一可能的三元组和为 0 。
提示：
3 <= nums.length <= 3000-105 <= nums[i] <= 10^5
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
}
};解析代码
建议看了上一篇：双指针⑥剑指 Offer 57. 和为s的两个数字再来看这一题，下一题还有四数之和。
与两数之和稍微不同的是，题目中要求找到所有「不重复」 的三元组。那我们可以利用在两数之和那里用的双指针思想，来对我们的暴力枚举做优化：先排序，然后固定- -个数a，在这个数后面的区间内，使用「双指针算法」快速找到两个数之和等于-a即可。但是要注意的是，这道题里面需要有「去重」操作，找到一个结果之后，left和right | 指针要「跳过重复」 的元素，当使用完一-次双指针算法之后，固定的a也要「跳过重复」的元素。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> ret;
sort(nums.begin(), nums.end());
int n = nums.size();
for(int i = 0; i < n;) // i是固定的数的下标
{
if(nums[i] > 0) // 小优化
{
break;
}
int left = i + 1, right = n - 1, target = -nums[i];
while(left < right)
{
int sum = nums[left] + nums[right];
if(sum < target)
{
++left;
}
else if(sum > target)
{
--right;
}
else
{
ret.push_back({nums[i], nums[left++], nums[right--]});
while(left < right && nums[left] == nums[left - 1]) // 去重
{
++left;
}
while(left < right && nums[right] == nums[right + 1])
{
--right;
}
}
}
++i;
while(i < n && nums[i] == nums[i - 1]) // 对i去重->for循环里不用++i了
{
++i;
}
}
return ret;
}
};⑧力扣18. 四数之和
难度 中等
给你一个由?n?个整数组成的数组?nums?，和一个目标值?target?。请你找出并返回满足下述全部条件且不重复的四元组?[nums[a], nums[b], nums[c], nums[d]]?（若两个四元组元素一一对应，则认为两个四元组重复）：
0 <= a, b, c, d?< na、b、c?和?d?互不相同nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按?任意顺序?返回答案 。
示例 1：
输入：nums = [1,0,-1,0,-2,2], target = 0 输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
示例 2：
输入：nums = [2,2,2,2,2], target = 8 输出：[[2,2,2,2]]
提示：
1 <= nums.length <= 200-10^9 <= nums[i] <= 10^9-10^9 <= target <= 10^9
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
}
};解析代码
建议看了前两篇再看这篇，解法（排序 + 双指针）：
算法思路：依次固定?个数 a，在这个数 a 的后面区间上，利用上力扣15. 三数之和，找到三个数，使这三个数的和等于 target - a 即可。
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> ret;
sort(nums.begin(), nums.end());
int n = nums.size();
for(int a = 0; a < n; )
{
for(int b = a + 1; b < n; )
{
long long target2 = (long long)target - nums[a] - nums[b];
int left = b + 1, right = n - 1;
while(left < right)
{
if(nums[left] + nums[right] < target2)
{
++left;
}
else if(nums[left] + nums[right] > target2)
{
--right;
}
else
{
ret.push_back({nums[a],nums[b],nums[left++],nums[right--]});
while(left < right && nums[left] == nums[left-1])
{
++left;
}
while(left < right && nums[right] == nums[right+1])
{
--right;
}
}
}
++b;
while(b < n && nums[b] == nums[b-1])
{
++b;
}
}
++a;
while(a < n && nums[a] == nums[a-1])
{
++a;
}
}
return ret;
}
};本篇完。
下一部分是滑动窗口算法的讲解和刷题，算法思路和双指针类似。
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码（1）
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- Java幼儿园学生信息管理系统（源码+开题）
- 旅游管理虚拟情景实训教学系统演示
- 推荐一下最近在看到比较好的小报童
- 探索 hasOwnProperty：处理对象属性的关键（下）
- 《长江丛刊》期刊投稿发表
- 网卡：初始化，frame组装，网卡处理电信号过程
- MetaAI语音翻译大模型Seamless登场，主打AI无缝同声传译
- SpringCloud之Seata基本介绍与安装
- 某系统模板注入漏洞分析
- MindOpt APL建模语言自定小义函数的重要性和示例