优化问题笔记（2）

发布时间：2023年12月18日

3. 约束优化问题的全局解

3.1 凸优化问题

局部解成为全局解的一类重要的优化问题是所谓凸优化问题. 我们称优化问题 $(f,\mathcal{D})$ 是凸的/拟凸的，是指 $f:\mathcal{D}\to\overline{\mathbb{R}}$ 是凸函数/拟凸函数. 称优化问题 $\begin{cases}\min f_0(x)\\[1ex]\text{s.t.} f_i(x)\le0,\quad i=1,\cdots,p,\\[1ex]h_j(x)=0,\quad j=1,\cdots,q,\\[1ex]x\in\Omega,\end{cases}$ 是凸的/拟凸的，是指它满足如下条件：

$(i)$ $f_0$ 是凸函数/拟凸函数；

$(ii)$ ${f_{i}\}_{i=1}^{p}$ 是凸函数;

$(iii)$ ${h_j\}_{j=1}^q$ 是仿射函数；

$(i v)$ $\Omega$ 为 $\mathbb{R}^n$ 中凸集.

显然，此时可行集 $\mathcal{D}$ 是凸集，( $f_0,\mathcal{D})$ 是凸问题/拟凸问题.

命题 4.3.1 (凸问题的局部解是全局解)

(1) 凸优化问题 $(f,\mathcal{D})$ 的局部解必为全局解.

(2) 拟凸问题 $(f,\mathcal{D})$ 的严格局部解必为严格全局解.

证.(1) 反证法：若 $x^*$ 是凸优化问题 $(f,\mathcal{D})$ 的局部解而不是全局解，则必存在 $x\in\mathcal{D}$ , 使得 $f(x)<f(x^*)$ .对任意的 $\theta\in(0,1)$ ,令 $x_\theta:=x^*+\theta(x-x^*)$ .显然 $x_\theta\in\mathcal{D}$ ,且当 $\theta$ 充分小时， $x_{\theta}$ 充分接近 $x^*$ ,从而 $f(x^*)\leq f(x_\theta)$ .于是 $\begin{aligned}f(x^*)\leq f(x_\theta)\leq(1-\theta)f(x^*)+\theta f(x)<(1-\theta)f(x^*)+\theta f(x^*)=f(x^*).\end{aligned}$ 矛盾.（上式中第二个不等号利用了凸函数的定义.）所以 $x^*$ 是全局解.

(2) 若 $x^*$ 是拟凸优化问题的 $(f,\mathcal{D})$ 的严格局部解而不是严格全局解，则存在 $x\in\mathcal{D}$ 使得 $f(x)\leq f(x^*)$ .沿用上面的符号，类似地，当 $\theta>0$ 充分小时，有 $f(x^*)<f(x_\theta)\leq\max\{f(x^*),f(x)\}=f(x^*).$ 矛盾. （上式中第二个不等号利用了拟凸函数的定义.）

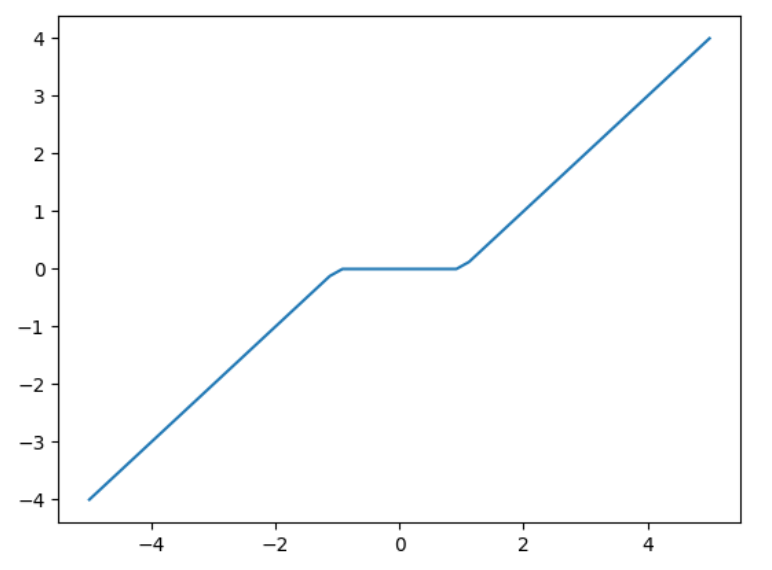
注：对于拟凸问题，非严格局部解未必是全局解. 例如函数 $f(x):=\begin{cases}x+1&x\leq-1\\0&x\in(-1,1)\\x-1&x\geq1\end{cases}$ 位于区间 (-1,1) 中每一点都是 $(f,\mathbb{R})$ 的局部最优解，但它们都不是全局最优解，如下图所示：

在这里插入图片描述
命题 3.1.2 (全局解与平稳点的等价性) 设凸优化问题 $(f,\mathcal{D})$ 的目标函数 $f$ 在 $x^*\in\mathcal{D}$ 处一阶可微， $x^*\in\mathcal{D}$ ,那么 $x^*$ 是 $(f,\mathcal{D})$ 的一个全局最优解当且仅当
$\begin{align}\nabla f(x^*)^T(x-x^*)&\ge0,\quad\forall x\in\mathcal{D}.\end{align}$
证. 必要性. $x^*\in\mathcal{D}$ 是一个最优解，因为 $\mathcal{D}$ 是凸集，由优化问题笔记 (1)中的命题 1.2.1有 $\nabla f(x^{*})^{T}d=0,\quad d^{T}\nabla^{2}f(x^{*})d\geq0,\quad\forall d\in V_{\mathcal{D}}$ ，以及由引理 1.2.2有 $\xi^T(x-x^*)\ge0,\forall x\in\mathcal{D} \iff \xi^Td\ge0,\forall d\in\mathbf{SFD}(x^*)$ ，于是可以推出(1)成立.

充分性. 设(1)成立. 则 $\forall x\in\mathcal{D}$ ,利用凸函数笔记 (1)中的命题 2.2.1,（下文直接引用，不再以链接形式给出笔记出处） $f\text{ 是凸函数当且仅当}f(y)\geq f(x)+\nabla f(x)^T(y-x),\quad\forall x,y\in\mathbf{dom}(f).$

于是有 $\begin{aligned}f(x)\geq f(x^*)+\nabla f(x^*)^T(x-x^*)\geq f(x^*).\end{aligned}$ 所以 $x^*$ 是 $(f,\mathcal{D})$ 的一个最优解.

注：当 $x^*\in\mathbf{ri}(\mathcal{D})$ 时，由引理 1.2.2 可知 (1)等价于 $\nabla f(x^*)\perp V_\mathcal{D}$ . 这意味着 $x^*$ 约束在 $V_\mathrm{D}$ 上是 $f$ 的一个平稳点( 满足 $\nabla f(x^*)=0$ 的点称为 $f$ 的平稳点).这一性质在优化问题的数值计算中非常重要，因为判断一个点是否为平稳点比判断其为局部极小点要容易得多.

例 3.1.1 设 $A\in\mathbb{R}^{m\times n},\quad b\in\mathbb{R}^m$ 使得集合 $\{x\in\mathbb{R}^n|Ax=b\}$ 非空. 又设函数 $f:\mathbb{R}^n\to\mathbb{R}$ 是可微的凸函数.那么， $x^*\in\mathbb{R}^n$ 是等式约束凸优化问题 $\begin{align} \begin{cases}\min f(x)\\\mathrm{s.t}\quad Ax=b\end{cases}\end{align}$ 的解当且仅当 $\nabla f(x^*)\in\mathbf{ran}(A^T),\quad Ax^*=b.$ 证.在 例 1.2.1 中已证明该可行集 $\mathcal{D}$ 满足： $\mathbf{ri}(D)=\mathcal{D}$ 且 $V_D=\mathbf{null}(A)=\mathbf{ran}(A^T)^\perp.$ 由命题 3.1.2 可知， $x^*\in\mathcal{D}$ 是优化问题 (2)的一个最优解当且仅当 $\nabla f(x^*)\in V_\mathcal{D}^\perp$ , 即 $\nabla f(x^*)\in\mathbf{ran}(A^T).$

3.2 二次优化问题

当目标函数和约束函数都是二次 (不超过二次) 函数时, $L (x, λ, μ)$ 关于 $x$ 也是二次函数,因而其 Taylor 展开式展开到二次项时余项为 0. 此时, 有如下全局解的充分条件.

命题 3.2.1 (二次优化问题全局解的充分条件) 对于不含约束集的约束优化问题 $\begin{cases}\min f_0(x)\\\mathrm{s.t}\quad f_i(x)\leq0,\quad i=1,\cdots,p,\\h_j(x)=0,\quad j=1,\cdots,q.&\end{cases}$ , 设 ${f_i\}_{i=0}^p,\{h_j\}_{j=1}^q$ 均为二次函数， $x^*\in\mathbb{R}^n$ ,存在 $\lambda^*\in\mathbb{R}^p,\mu^*\in\mathbb{R}^q$ ,满足 $KK T$ 条件 $\begin{cases}x^*\in\mathcal{D};\\\lambda_i^*\geq0,\quad i=1,\cdots,p;\\\lambda_i^*f_i(x^*)=0,\quad i=1,\cdots,p;\\\nabla_xL(x^*,\lambda^*,\mu^*)=0.\end{cases}$ ,且有下式： $\begin{align} (x-x^*)^T\nabla_x^2L(x^*,\lambda^*,\mu^*)(x-x^*)\geq0,\quad\forall x\in\mathcal{D}\end{align}$ 则 $x^*$ 是一个全局最优解.

证.对任意的 $x\in\mathcal{D}$ ,记 $d:=x-x^*$ ,那么
$\begin{aligned} \begin{aligned}f_0(x)\geq L(x,\lambda^*,\mu^*)\end{aligned}& =L(x^*,\lambda^*,\mu^*)+d^T\nabla_xL(x^*,\lambda^*,\mu^*)+\frac12d^T\nabla_x^2L(x^*,\lambda^*,\mu^*)^Td \\ &\geq L(x^{*},\lambda^{*},\mu^{*})=f_{0}(x^{*}). \end{aligned}$ 所以 $x^*$ 是一个全局最优解.

注：当 $x^*$ 是一个正则点时，根据 定义 2.1.3 有 $\mathcal{T}(x^*)\cap\partial B(0,1)\subset\mathbf{LFD}(x^*)=\mathbf{SFD}(\overline{x^*)}$ .根据 引理 1.2.2 可知，本命题的条件(3) 比局部解的二阶必要条件 $d^T\nabla_x^2L(x^*,\lambda^*,\mu^*)d\geq0,\quad\forall d\in\mathcal{T}(x^*)$ 要强.

3.3 无约束二次优化问题

命题 3.3.1 (二次函数之最优解的条件) 设 $f(x):=\frac12x^TAx+b^Tx$ , 其中 $A$ 是 $n$ 阶实对称矩阵， $x^*\in\mathbb{R}^n$ .那么，对于无约束优化问题 $(f,\mathbb{R}^n)$ ,即问题 $\begin{cases}\min f_0(x)\\\mathrm{s.t}\quad f_i(x)\leq0,\quad i=1,\cdots,p,\\h_j(x)=0,\quad j=1,\cdots,q.&\end{cases}$ ,如下三条相互是等价的：

$3.3.1.1)\:x^*$ 是 $f$ 的一个全局极小点；

$3.3.1.2)\:x^*$ 是 $f$ 的一个局部极小点；

$(3.3.1.3) A$ 是半正定矩阵且 $Ax^*+b=0.$

证.根据全局最小点和局部极小点的定义可以知道， (3.3.1.1) 蕴含 (3.3.1.2). 对 $f$ 计算可得 $\begin{align} \begin{aligned}\nabla f(x^*)=Ax^*+b,\quad\nabla^2f(x^*)=A.\end{aligned}\end{align}$ 因此，若 (3.3.1.2) 成立，那么，由 必要性命题 1.2.1：若 $f$ 在 $x^*$ 处二阶连续可微，且 $x^*\in\mathbf{ri}(\mathcal{D})$ ,则 $\nabla f(x^{*})^{T}d=0,\quad d^{T}\nabla^{2}f(x^{*})d\geq0,\forall d\in V_{\mathcal{D}}.$ 即知 (3.3.1.3) 成立.

设 (3.3.1.3)成立. 利用(4)可知 $\nabla f(x^*)=0$ ,且 $\nabla^2f(x^*)$ 半正定. 于是， $\forall x\in\mathbb{R}^n$ ,做Taylor 展开，有 $f(x)=f(x^*)+\frac12(x-x^*)^TA(x-x^*)\geq f(x^*).$ 所以 $x^*$ 是 $f$ 在 $\mathbb{R}^n$ 上的最小点. 即(3.3.1.1) 成立.

注：二次函数 $f(x):=\frac12x^TAx+b^Tx$ 未必总存在极小值点. 事实上，当 $A$ 不是半正定矩阵时，或者 $A$ 半正定但 $A x + b = 0$ 无解时， $f (x)$ 就不存在极小值点. 此时， $\inf_{x\in\mathbb{R}^n}f(x)=-\infty$ .例如，对于 $A=\begin{bmatrix}0&0\\0&1\end{bmatrix},\quad b:=\begin{bmatrix}b_1\\0\end{bmatrix},\quad c=0,$ 有 $f(x)=\frac12x_2^2+b_1x_1,\:x:=(x_1,x_2)^T\in\mathbb{R}^2$ .当 $b_1\neq0$ 时， $f (x)$ 不存在最小值点.

推论 3.3.1 (二次函数之全局最优解存在的条件) 设 $A$ 是 $n$ 阶实对称矩阵，那么，二次函数 $f(x):=\frac12x^TAx+b^Tx$ 在 $\mathbb{R}^n$ 上有最小值点当且仅当 $f (x)$ 在 $\mathbb{R}^n$ 上有下界.

证.将 $A$ 做特征分解 $A=U\Lambda U^T$ ,其中 $U$ 是一个 $n$ 阶正交矩阵， $\Lambda=\mathbf{diag}(\lambda_1,...,\lambda_n)$ , 其中 $\lambda_1\geq...\geq\lambda_n$ 是 $A$ 的全部特征值. 令 $y:=U^Tx,~q:=U^Tb$ , 那么
$f(x)=\frac12y^T\Lambda y+q^Ty=\frac12\sum_{i=1}^n(\lambda_iy_i^2+2q_iy_i).$ 所以 $f (x)$ 在 $\mathbb{R}^n$ 上有下界当且仅当对每一个 $1\leq i\leq n$ , 单变量函数 $g_i(y):=\lambda_iy^2+2q_iy$ 在 R 上有下界.即 $\lambda_i\geq0$ 且 $\lambda_i=0$ 时，有 $q_i=0$ . 此时，当 $y_i:=\begin{cases}-\frac{q_i}{\lambda_i}&\lambda_i>0,\\\text{任意值}&\lambda_i=0,&\end{cases}\quad i=1,...,n.$ 时， $x = U y$ 是 $f (x)$ 在 $\mathbb{R} ^n$ 上的一个最小值点.

例 3.3.1 (最小二乘问题 (LSP: Least Square Problem)) 给定矩阵 $A\in\mathbb{R}^{m\times n}$ 和向量 $b\in\mathbb{R}^m$ , 如下无约束优化问题 $\begin{align} \min\|Ax-b\|_2^2\end{align}$ 称为最小二乘问题. $x^*$ 是其最优解当且仅当 $A^TA)x^*=A^Tb$ . 该问题的解一定存在且构成一个 $n ? r$ 维仿射空间，其中 $\mathbf{rank}( A)$

证.计算可得 $Ax-b\|_2^2=x^T(A^TA)x-2b^TAx+\|b\|_2^2,$ 根据线性代数的内容，假设 $A$ 的列向量分别是 $\alpha_1,\cdots,\alpha_n$ ，那么有： $\begin{aligned} |AX_{0}-b|\text{ 最小}& \Longleftrightarrow\text{对于任意的 }X\text{ 都有 }|AX_0-b|\leq|AX-b| \\ &\Longleftrightarrow AX_0-b\perp U\text{ 其中 }U=\{AX|X\in\mathbb{R}^n\}=L(\alpha_1,\cdots,\alpha_n) \\ &\Longleftrightarrow AX_0-b\perp\alpha_i(i=1,2,\cdots,n) \\ &\Longleftrightarrow\alpha_i'(AX_0-b)=0(i=1,2,\cdots,n) \\ &\left.\Longleftrightarrow\left(\begin{array}{c}\alpha_1'\\\vdots\\\alpha_n'\end{array}\right.\right)(AX_0-b)=0 \\ &\Longleftrightarrow A^{\prime}(AX_{0}-b)=0 \\ &\Longleftrightarrow A^{\prime}AX_{0}=A^{\prime}b. \end{aligned}$ 记 $\mathbf{rank}( A)$ ，即 $r$ 表示矩阵的秩

一方面 $r(A^{\prime}A,A^{\prime}b)=r(A^{\prime}(A,b))\leq r(A^{\prime})=r(A).$ 另一方面 $r(A^{\prime}A,A^{\prime}b)\geq r(A^{\prime}A)=r(A),$ 这就说明 $r(A^{\prime}A,A^{\prime}b)=r(A)=r(A^{\prime}A).$

所以线性方程组 $A^TA)x\:=\:A^Tb$ 有解，且其解就是上述最小二乘问题的解.

根据上面的推导可以知道，该线性方程组的增广矩阵 $A^TA,A^Tb)=A^T(A,b)$ 的秩就等于 $\mathbf{rank}(A^T)=r=\mathbf{rank}(A^TA),$ 所以该线性方程组有解，其有 $n ? r$ 个基向量，且解空间构成一个 $n ? r$ 维仿射空间.

3.4 一个典型的二次等式约束二次优化问题

给定 $n$ 阶对称矩阵 $A ， B$ ，考虑如下的优化问题： $\begin{align}\begin{cases}\min x^TAx\\\mathrm{s.t~}x^Tx=1,\\x^TBx=1.&\end{cases}\end{align}$ 记 $\mathcal{D}:=\{x\in\mathbb{R}^n|x^Tx=1,x^TBx=1\}$ ，当 $\mathcal{D}$ 非空时, 根据函数的连续性可知该优化问题的全局最优解是存在的.

若 $x^? ∈ \mathcal{D}$ 是问题(6)的全局解, 且 $\left \{ x^?, Bx^? \right \}$ 线性无关, 根据局部解的二阶必要条件 (命题 2.2.5),存在 $\alpha^*,\beta^*\in\mathbb{R}$ , 使得 $\begin{align} Hx^*=0,\quad d^THd\geq0,\quad\forall d\in\mathcal{T}(x^*),\end{align}$ 其中， $\mathcal{T}(x^*):=\left(\mathbf{span}\{x^*,Bx^*\}\right)^\perp$ 是问题(6) 的约束条件的切空间，而根据命题 3.2.1当 $\begin{align} Hx^*=0,\quad d^THd\geq0,\quad\forall d\in\mathcal{D}-x^*,\end{align}$ 时， $x^*$ 是问题(6)全局解.

下面命题则可以说明必要条件可以加强为 $Hx^*=0,~H\succeq0.$

命题 3.4.1 (Bar-on and Grasse) 设 $x^*\in\mathcal{D}$ ,且使得 ${x^*,Rx^*\}$ 线性无关，则 $x^*$ 是问题(6)的全局解当且仅当存在 $\alpha^*,\beta^*\in\mathbb{R}$ , 使得(8)所定义的 $H$ 满足： $\begin{align} Hx^*=0,\quad H\succeq0.\end{align}$

Reference

包括但不限于以下内容：

(1)Stephen Boyd, Stephen P Boyd, and Lieven Vandenberghe. Convex
optimization. Cambridge university press, 2004.

(2) JR Bar-On and KA Grasse. Global optimization of a quadratic functional with quadratic equality constraints. Journal of Optimization Theory and Applications, 82(2):379–386, 1994.

(3) JR Bar-On and KA Grasse. Global optimization of a quadratic functional with quadratic equality constraints, part 2. Journal of Optimization Theory and Applications, 93(3):547–556, 1997.

文章来源:https://blog.csdn.net/weixin_47255403/article/details/135056154
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若内容造成侵权/违法违规/事实不符，请联系我的编程经验分享网邮箱：chenni525@qq.com进行投诉反馈，一经查实，立即删除！