【数据结构】归并排序的两种实现方式与计数排序

前言：在前面我们讲了各种常见的排序，今天我们就来对排序部分收个尾，再来对归并排序通过递归和非递归的方法进行实现，与对计数排序进行简单的学习。

💖 博主CSDN主页:卫卫卫的个人主页 💞
👉 专栏分类:数据结构 👈
💯代码仓库:卫卫周大胖的学习日记💫
💪关注博主和博主一起学习!一起努力！

---

C语言排序算法 - 归并排序与计数排序

归并排序 - 递归模拟实现

归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide andConquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。 归并排序核心步骤。

1. 分解将数组中的元素分成两个部分，再将那俩个部分分成两个部分，直到分成只剩一个元素不能分解为止。
2. 将分解后的元素，俩俩依次归并，并且再归并的过程中对齐进行排序，因此归并完成的时候也就排序完成了（如下图所示）。
   

---

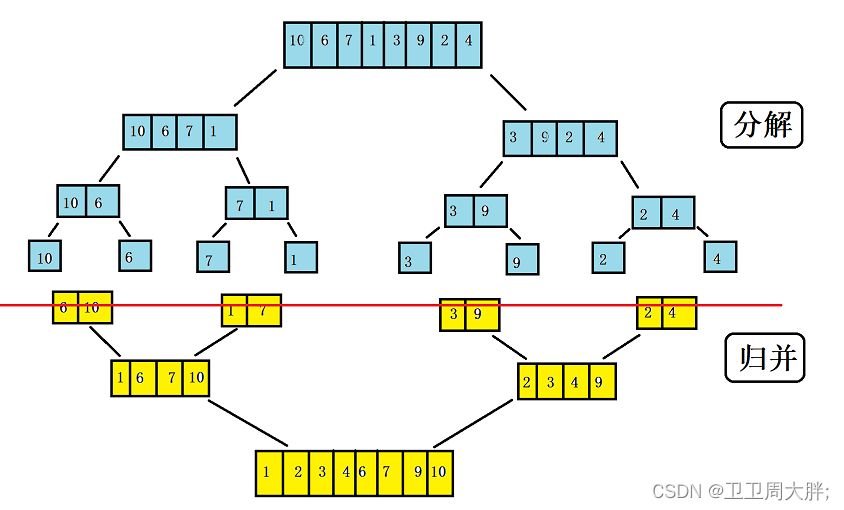
归并排序的实现步骤

1. 将俩个有序数列合并后进行排序。
2. 开辟一块临时空间存间，将两个序列中的较小值依次放入，当有一个序列走到其尾部的时候，退出循环结束排序。
3. 我们需要考虑当一个数列走到尾部的时候但另一个序列并没有完成排序情况，因此找到那个没有走完的数列让其直接全部尾插到开辟的临时空间的尾部即可(如下图所示)。
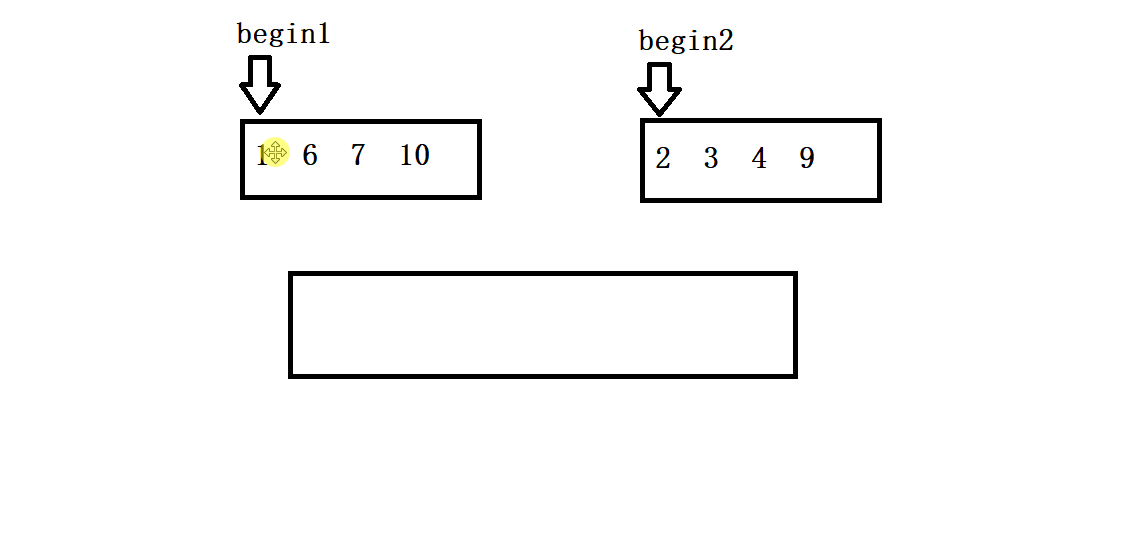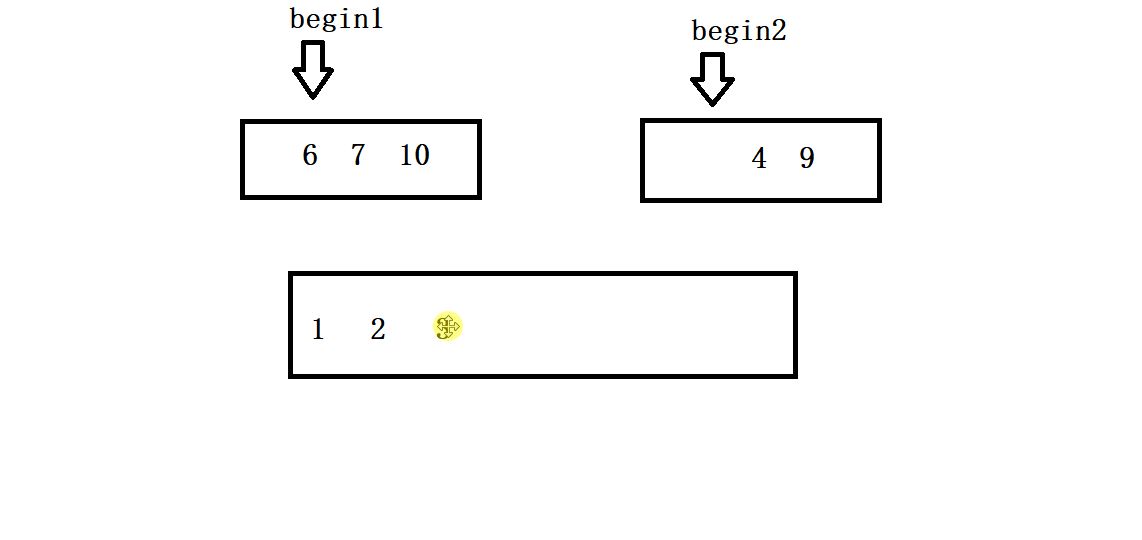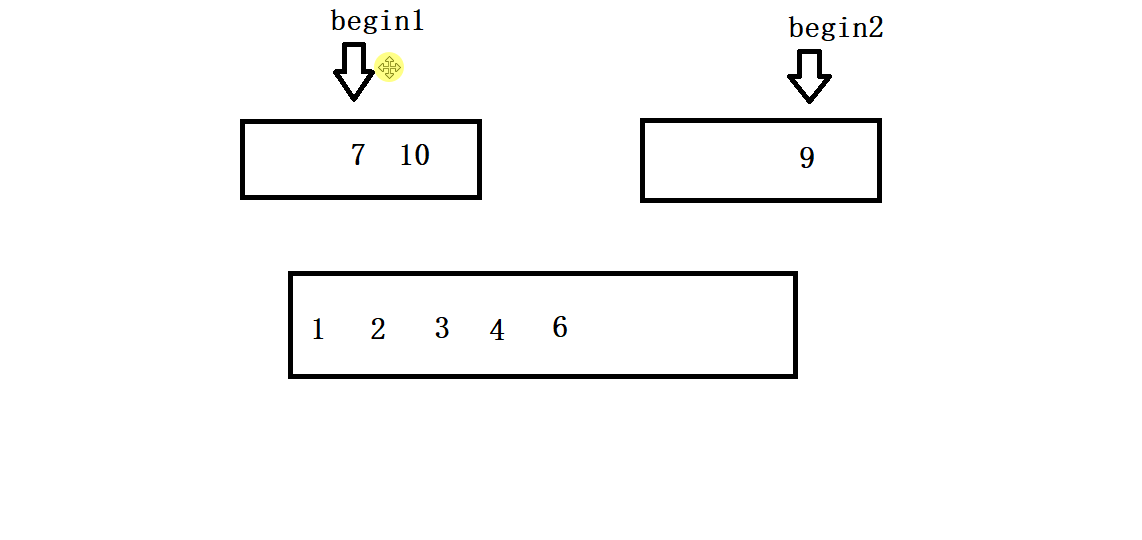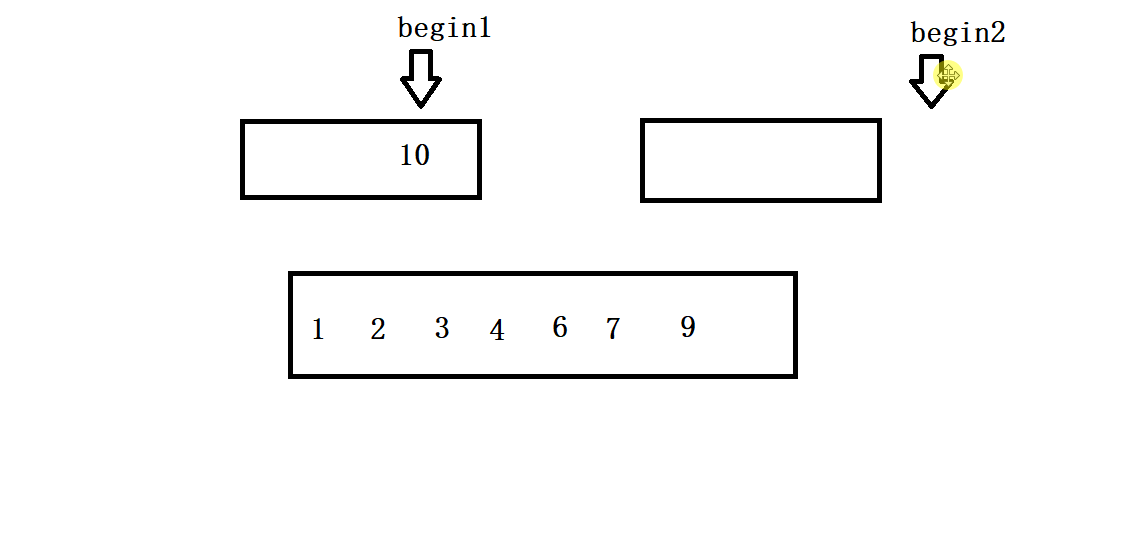
4. 归并排序是一个非常经典的分治问题，因此我们通过递归把数组不断分为俩个部分然后依次对其进行排序

代码实现:

void _MergeSort(int* a, int begin,int end,int* tmp)//归并排序
{
	if (begin >= end)
		return;
	int mid = (begin + end) / 2;
	_MergeSort(a, begin, mid, tmp);//分为左半边 a[begin] | a[mid]
	_MergeSort(a, mid + 1, end, tmp);
	int begin1 = begin;
	int begin2 = mid + 1;
	int i = begin1;
	int end1 = mid;
	int end2 = end;
	while (begin1 <= end1 && begin2 <= end)//排序
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}//此时可能出现没有走完的情况
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end)
	{
		tmp[i++] = a[begin2++];
	}
	memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));//拷贝回去

}



void MergeSort(int* a, int n)
{
	assert(a);
	int* tmp = (int*)malloc(sizeof(int) * n);//开辟临时空间
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	_MergeSort(a, 0, n - 1, tmp);
	free(tmp);
}

函数测试:

void Test_MergeSort()
{
	int a[] = { 1,2,30,0,99,1,7,8,2,11,0,3,13 };
	MergeSort(a, sizeof(a) / sizeof(a[0]));
	PrintArray(a, sizeof(a) / sizeof(a[0]));

}

int main()
{
	Test_MergeSort();
}

运行结果:

---

归并排序-非递归模拟实现

归并排序的非递归实现是非常复杂的一个算法，在快速排序中我们使用栈来存储待排数组的左右区间，模拟递归的过程，然而在归并排序中我们无非用栈来实现，因为我们无非将分解后的区间在通过栈来合并，因此我们在归并排序中不能这么实现。
实现思路:

1. 还记得我们在递归实现的过程中是将其直接拆分成无法再进行拆分的单个元素嘛？我们在这直接通过一个gap将这个数组直接看成拆分后的数组，然后直接对其进行归并。
2. 我们将间距为1的数组依次合并后，我们在让gap变为4，然后再对这一数组元素进行依次合并，然后以此类推直到gap比我们的数组的元素个数还大时停止排序即可。
3. 我们需要考虑边界问题，即数组中的元素不一定总是二的倍数，因此我们需要考虑第一个数组越界，第二个数组全部越界和第二个数组部分越界这三种情况。下图是对gap为1的部分图
   

---

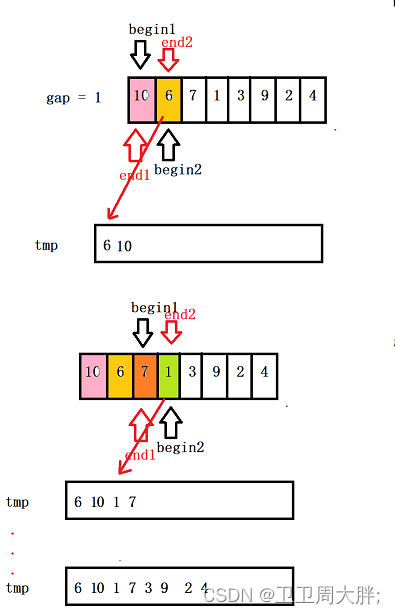
代码实现:

void MergeSortNoR(int* a, int n)//归并排序 -- 非递归
{
	int* tmp = (int*)malloc( n * sizeof(int));
	int gap = 1;
	while (gap < n)
	{
		int i = 0;
		for (i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;//第一个数组的区间
			int begin2 = i + gap, end2 = i + 2 * gap - 1;//此时第二个数组的区间
			if (end1 >= n)
				break;
			if (begin2 >= n)
				break;
			if (end2 >= n)
				end2 = n - 1;
			int j = i;//此时合并数组
			while (begin1 <= end1 && begin2 <= end2)//排序
			{
				if (a[begin1] <= a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}//此时可能出现没有走完的情况
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			memcpy(a + i, tmp + i, (end2 - i + 1) * sizeof(int));//拷贝回去
		}
		gap *= 2;
	}
	

}

函数测试:

void Test_MergeSortNoR()
{
	int a[] = { 1,2,30,0,99,1,7,8,2,3 };
	MergeSortNoR(a, sizeof(a) / sizeof(a[0]));
	PrintArray(a, sizeof(a) / sizeof(a[0]));
}
int main()
{
	Test_MergeSortNoR();
	return 0;
}

运行结果:

---

计数排序

计数排序是一种非比较排序算法，它的基本思想是统计每个元素在待排序序列中出现的次数，然后依次按照元素值的大小，将元素按照出现的次数放入有序序列中。计数排序是一种稳定排序算法，但是它只适用于元素取值范围较小且分布较均匀的情况

1. 统计元素出现的次数：遍历待排序序列，统计每个元素出现的次数，并记录在一个辅助数组中(通常辅助数组的大小为最大元素的大小)。

2. 计算元素的位置：根据元素出现次数的累加值，计算出每个元素在有序序列中的位置。

3. 将元素放入有序序列中：根据元素的位置，将元素依次放入有序序列中。

4. 将辅助数组中计数不为0的数依次传给原数组，此时即可完成排序.
   

---

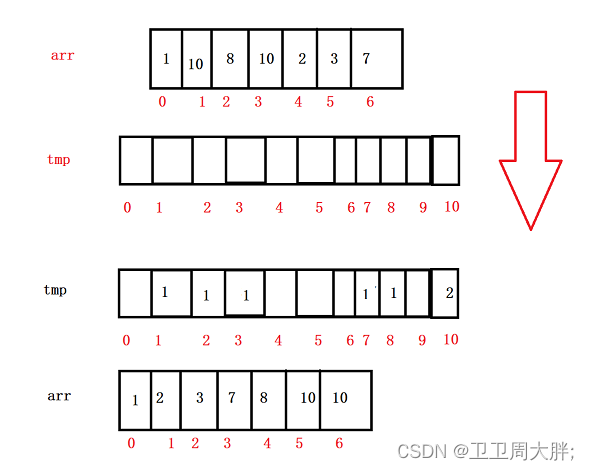
代码实现:

void CountSort(int* a,int n)//计数排序
{
	int max = a[0];
	int min = a[0];
	int i = 0;
	for (i = 0; i < n; i++)
	{
		if (max < a[i])
			max = a[i];
		if (min > a[i])
			min = a[i];
	}
	int* tmp = (int*)calloc(max+1 ,4);
	if (tmp == NULL)//如果空间申请失败，报个错，并中止程序
	{
		perror("calloc");
		return;
	}

	for (i = 0; i < n; i++)
	{
		tmp[a[i]]++;
	}

	int j = 0;
	for (i = 0; i < max + 1; i++)
	{
		while (tmp[i])
		{
			a[j++] = i;
			tmp[i]--;
		}
	}

}

函数测试:

void Test_CountSort()
{
	int a[] = { 1,0,0,2,333,3,0,99 };

	CountSort(a, sizeof(a) / sizeof(a[0]));
	PrintArray(a, sizeof(a) / sizeof(a[0]));

}
int main()
{
	Test_CountSort();

}

运行结果:

---

我们思考一下，如果数组每次都是开辟最大的元素的个数的时候是不是会照成空间上的一种浪费？并且如果我们需要存储有负数的时候我们又该怎么办？解决办法

1. 我们找到数组中的最大值和最小值，让其相减，此时我们让其数组中的每个元素都可以因此往前挪动了，即最小值无论它是多少它都会在0这个位置，最大值也会在其相对映射的地方。
2. 同理开辟最大值减去最小值加1的空间即可，并不需要额外再多开辟空间。

代码优化实现:

void CountSort(int* a,int n)//计数排序
{
	int max = a[0];
	int min = a[0];
	int i = 0;
	for (i = 0; i < n; i++)
	{
		if (max < a[i])
			max = a[i];
		if (min > a[i])
			min = a[i];
	}
	int range = max - min + 1;
	int* tmp = (int*)calloc(range ,4);
	if (tmp == NULL)//如果空间申请失败，报个错，并中止程序
	{
		perror("calloc");
		return;
	}

	for (i = 0; i < n; i++)
	{
		tmp[a[i] - min]++;
	}

	int j = 0;
	for (i = 0; i < range; i++)
	{
		while (tmp[i])
		{
			a[j++] = i + min;
			tmp[i]--;
		}
	}

}

函数测试:

void Test_CountSort()
{
	int a[] = { 1,-1,-3,-10,0,2,333,3,0,-3,99 };

	CountSort(a, sizeof(a) / sizeof(a[0]));
	PrintArray(a, sizeof(a) / sizeof(a[0]));

}

运行结果

---

结语：今天的内容就到这里吧，谢谢各位的观看，如果有讲的不好的地方也请各位多多指出，作者每一条评论都会读的，谢谢各位。

---

🫵🫵🫵 这里也祝各位寒假快乐哦 💞