Lucas求大组合数C(n,m)%p
发布时间:2024年01月18日
将大组合数C(n,m)%p分解为小组合数C(n,m)%p乘积的模,n<=10^18,m<=10^18。
其中求解小组合数可以根据定义式计算(质因子分解),也可以通过定义式的变形计算(逆元)
一、定义式计算(质因子分解-快速幂)
快速幂计算每一组pi^ci%p,然后相乘取模
#include<stdio.h>
//素数表(筛法)
const int maxn=1000000;
int prime[maxn];
int pNum=0;
bool p[maxn]={false};
void Find_Prime(){
for(int i=2;i<maxn;i++){
if(p[i]==false){
prime[pNum++]=i;
for(int j=i+i;j<maxn;j+=i){
p[j]=true;
}
}
}
}
//n!中含质因子p个数
int cal(int n,int p){
int ans=0;
while(n){
ans+=n/p;
n/=p;
}
return ans;
}
//快速幂求a^b%p
typedef long long LL;
LL binaryPow(LL a,LL b,LL m){
if(b==0) return 1;
if(b&1) return a*binaryPow(a,b-1,m)%m;
else{
LL mul=binaryPow(a,b/2,m);
return mul*mul%m;
}
}
//小组合数C(n,m)%p
//遍历素数表中每一个质因子,计算每一组pi^ci%p,然后相乘取模
int C(int n,int m,int p){
int ans=1;
for(int i=0;prime[i]<=n;i++){
int c=cal(n,prime[i])-cal(m,prime[i])-cal(n-m,prime[i]); //C(n,m)中含质因子个数
ans=ans*binaryPow(prime[i],c,p)%p;
}
return ans;
}
//Lucas定理求大组合数C(n,m)%p
int Lucas(int n,int m,int p){
if(m==0) return 1;
return C(n%p,m%p,p)*Lucas(n/p,m/p,p)%p;
}
int main(){
Find_Prime();
int n,m,p;
scanf("%d%d%d",&n,&m,&p);
printf("%d",Lucas(n,m,p));
return 0;
}二、定义式的变形计算(逆元)
#include<stdio.h>
//扩展欧几里得(解出x)
int exGcd(int a,int m,int &x,int &y){
if(m==0){
x=1;
y=0;
return a;
}
int g=exGcd(m,a%m,x,y);
int temp=x;
x=y;
y=temp-(a/m)*y;
return g;
}
//逆元(得0-m范围内的解)
int inverse(int a,int m){
int x,y;
int g=exGcd(a,m,x,y);
return (x%m+m)%m;
}
//求小组合数C(n,m)%p
int C(int n,int m,int p){
int ans=1;
for(int i=1;i<=m;i++){
ans=ans*(n-m+i)%p;
ans=ans*inverse(i,p)%p;
}
return ans;
}
//Lucas求大组合数 C(n,m)%p
int Lucas(int n,int m,int p){
if(m==0) return 1;
return C(n%p,m%p,p)*Lucas(n/p,m/p,p)%p;
}
int main(){
int n,m,p;
scanf("%d%d%d",&n,&m,&p);
printf("%d",Lucas(n,m,p));
return 0;
}运行结果:
C(84,58)%5=2
?
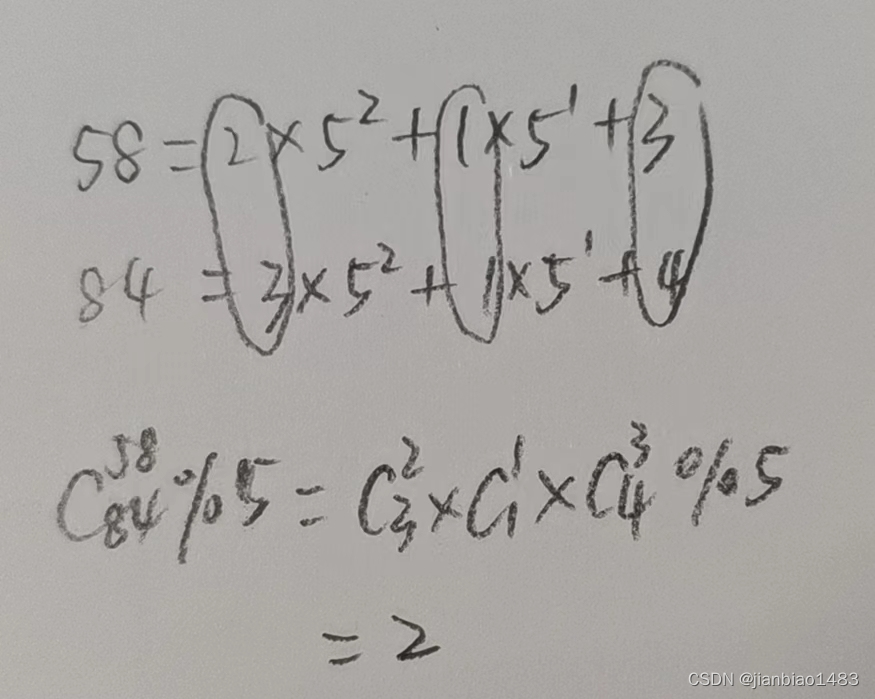
文章来源:https://blog.csdn.net/jianbiao1483/article/details/135668824
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- ZKP Algorithms for Efficient Cryptographic Operations 1 (MSM & Pippenger)
- postgresql可视化导入csv文件
- YOLOv8独家改进:IoU系列篇 | Focaler-IoU???????更加聚焦的IoU损失Focaler-IoU |2024年最新发表
- SpringBoot整合JWT+Spring Security+Redis实现登录拦截(一)
- 城市酷选模式开发(门店免单排队返利系统)
- HNU-编译原理-期末复习(刷题)
- 鸿蒙OS应用开发之点击事件
- linux环境开发工具---yum与vim
- SpringBoot
- AD采集卡设计方案:630-基于PCIe的高速模拟AD采集卡