leetcode算法题之递归--综合练习(一)
发布时间:2024年01月06日
此专题对我们之前所学的关于递归的内容进行一个整合,大家可以自行练习,提升自己的编码能力。
1.找出所有子集的异或总和在求和
class Solution {
int ret =0;
int path =0;
public:
int subsetXORSum(vector<int>& nums) {
dfs(nums,0);
return ret;
}
void dfs(vector<int>& nums,int pos)
{
ret += path;
for(int i=pos;i<nums.size();i++)
{
path ^= nums[i];
dfs(nums,i+1);
path ^= nums[i];//异或的消消乐原理
}
}
};
2.全排列II
class Solution {
vector<vector<int>> ret;
vector<int> path;
bool check[9];
public:
vector<vector<int>> permuteUnique(vector<int>& nums) {
sort(nums.begin(),nums.end());
dfs(nums,0);
return ret;
}
// //法一:只关心不合法的,也就是不满足全排列要求的都剪枝掉
// void dfs(vector<int>& nums,int pos)
// {
// if(pos == nums.size())
// {
// ret.push_back(path);
// return;
// }
// for(int i=0;i<nums.size();i++)
// {
// if(check[i] == true||(i!=0&&nums[i] == nums[i-1]&&check[i-1] == false))
// {
// continue;
// }
// path.push_back(nums[i]);
// check[i] = true;
// dfs(nums,pos+1);
// path.pop_back();
// check[i] = false;
// }
// }
//法二:只关心合法的,也就是满足全排列要求的
void dfs(vector<int>& nums,int pos)
{
if(pos == nums.size())
{
ret.push_back(path);
return;
}
for(int i=0;i<nums.size();i++)
{
if(check[i] == false&&(i==0||nums[i]!=nums[i-1]||check[i-1] == true))
{
path.push_back(nums[i]);
check[i] = true;
dfs(nums,pos+1);
path.pop_back();
check[i] = false;
}
}
}
};
3.电话号码的字母组合
class Solution {
string path;
vector<string> ret;
string hash[10] = {"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
public:
vector<string> letterCombinations(string digits) {
if(digits.size() == 0)
{
return ret;
}
dfs(digits,0);
return ret;
}
void dfs(string& digits, int pos)
{
if(pos == digits.size())
{
ret.push_back(path);
return;
}
for(auto ch:hash[digits[pos]-'0'])
{
path.push_back(ch);
dfs(digits,pos+1);
path.pop_back();
}
}
};
4.括号生成
class Solution {
vector<string> ret;
string path;
int left,right,n;
public:
//策略:左括号的数量等于右括号的数量
//从头开始,左括号的数量大于等于右括号的数量
vector<string> generateParenthesis(int _n) {
n = _n;
dfs();
return ret;
}
void dfs()
{
if(right == n)
{
ret.push_back(path);
return;
}
if(left<n)
{
path.push_back('(');
left++;
dfs();
path.pop_back();
left--;
}
if(left>right)
{
path.push_back(')');
right++;
dfs();
path.pop_back();
right--;
}
}
};
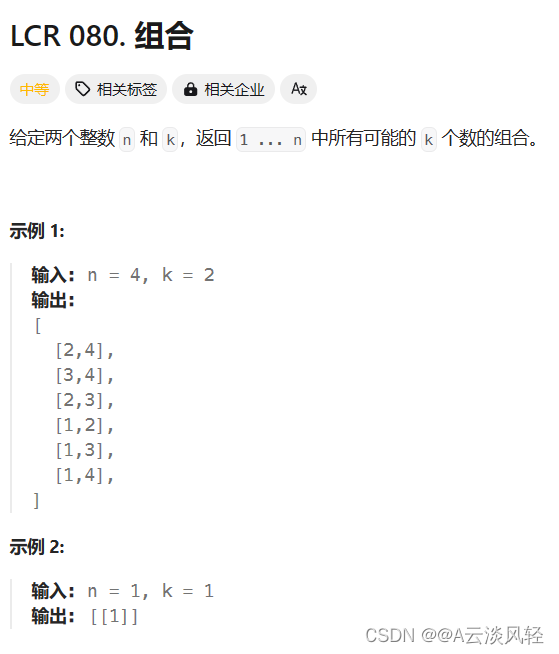
5.组合
class Solution {
vector<vector<int>> ret;
vector<int> path;
int n,k;
public:
vector<vector<int>> combine(int _n, int _k) {
n = _n,k=_k;
dfs(1);
return ret;
}
void dfs(int pos)
{
if(path.size() == k)
{
ret.push_back(path);
}
for(int i=pos;i<=n;i++)
{
path.push_back(i);
dfs(i+1);
path.pop_back();
}
}
};
6.目标和
class Solution {
int ret;
int aim;
int n;
public:
int findTargetSumWays(vector<int>& nums, int target) {
aim = target;
n = nums.size();
dfs(nums,0,0);
return ret;
}
void dfs(vector<int>& nums,int pos,int path)
{
//path做参数
if(pos == nums.size())
{
if(path == aim)
{
ret++;
}
return;
}
dfs(nums,pos+1,path+nums[pos]);
dfs(nums,pos+1,path-nums[pos]);
}
};
class Solution {
int ret;
int aim;
int path;
int n;
public:
int findTargetSumWays(vector<int>& nums, int target) {
aim = target;
n = nums.size();
dfs(nums,0,0);
return ret;
}
void dfs(vector<int>& nums,int pos,int path)
{
//path做全局变量
if(pos == nums.size())
{
if(path == aim)
{
ret++;
}
return;
}
path +=nums[pos];
dfs(nums,pos+1,path);
path -= nums[pos];
path -= nums[pos];
dfs(nums,pos+1,path);
path += nums[pos];
}
};
7.组合总和
class Solution {
vector<vector<int>> ret;
vector<int> path;
int aim;
public:
vector<vector<int>> combinationSum(vector<int>& c, int target) {
aim = target;
dfs(c,0,0);
return ret;
}
void dfs(vector<int>& c,int pos,int sum)
{
if(sum>aim) return;
if(sum == aim)
{
ret.push_back(path);
return;
}
for(int i=pos;i<c.size();i++)
{
path.push_back(c[i]);
dfs(c,i,sum+c[i]);
path.pop_back();
}
}
};
8.字母大小写全排列
class Solution {
vector<string> ret;
string path;
public:
vector<string> letterCasePermutation(string s) {
dfs(s,0);
return ret;
}
void dfs(string& s,int pos)
{
if(pos == s.size())
{
ret.push_back(path);
return;
}
if(s[pos]<'0' || s[pos]>'9')
{
//变
path.push_back(change(s[pos]));
dfs(s,pos+1);
path.pop_back();
}
//不变
path.push_back(s[pos]);
dfs(s,pos+1);
path.pop_back();
}
char change(char ch)
{
if(ch>='a'&&ch<='z') ch -= 32;
else ch += 32;
return ch;
}
};
9.优美的排列
class Solution {
bool check[16];
int ret;
int n;
public:
int countArrangement(int _n) {
n = _n;
dfs(1);
return ret;
}
void dfs(int pos)
{
if(pos == n+1)
{
ret++;
return;
}
for(int i=1;i<=n;i++)
{
if(!check[i] && (i%pos ==0 || pos%i == 0))
{
check[i] = true;
dfs(pos+1);
check[i] = false;
}
}
}
};
文章来源:https://blog.csdn.net/m0_55283616/article/details/135422847
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。 如若内容造成侵权/违法违规/事实不符,请联系我的编程经验分享网邮箱:chenni525@qq.com进行投诉反馈,一经查实,立即删除!
最新文章
- Python教程
- 深入理解 MySQL 中的 HAVING 关键字和聚合函数
- Qt之QChar编码(1)
- MyBatis入门基础篇
- 用Python脚本实现FFmpeg批量转换
- SpringBoot-整合MyBatis
- Spring事件机制之ApplicationEvent
- Ubuntu的安装和配置ssh
- 【算法每日一练]-图论(保姆级教程篇14 )#会议(模板题) #医院设置 #虫洞 #无序字母对 #旅行计划 #最优贸易
- c++入门
- 浅析位运算符(左移、右移、与、或、异或)
- 攸信UMS工业配送AMR F1引领智能物流发展,侨智大会瞩目焦点
- yolov8 opencv dnn部署 github代码
- 第七章 虚拟机类加载机制
- 【SOC的多种计算方法】